GRACE数据反演的新理解

一、问题提出

“重力恢复与气候实验”（GRACE）为监测地球系统内全球大尺度质量变化提供了一种新途径。自2002年3月发射以来，GRACE一直在生成时间变化的重力场模型，这些模型可用于量化与全球气候变化相关的地球系统不同组成部分内的质量再分配，包括陆地水储存（TWS）变化，海平面变化，以及极地冰盖和山地冰川的冰质量平衡。GRACE还提供了衡量与大地震相关的质量变化的独特手段，并在研究地震形变（特别是对于海洋地震）方面为地球表面测量提供了有效补充。除了重力场模型外，最近，GRACE还生成了时间变化的mascon解，直接表示地表质量变化。

GRACE的Level-2产品，即以完全归一化球谐（SH）系数形式发布的月度SH重力场解，已被广泛用于研究地球内外的质量变化。月度SH系数可以转换为等效水高（EWH）变化（Wahr et al.，1998），然后用于表示全球质量再分配。然而，从重力场变化反演到质量再分配是不唯一的。因此，必须假设质量变化发生在地球表面上，以从GRACE的时间变化重力场推断出EWH变化（Wahr et al.，1998）。由于GRACE观测中大部分主要的重力变化信号来自发生在地球表面上的地球物理过程（例如，陆地水运输和冰融化），这种2-D假设已经被证明在各种应用中是地球现实的很好表示。同时，还假设地球是一个球体，以简化并使得从GRACE SH系数到EWH变化的推导成为可能（Wahr et al.，1998），这个假设认为质量变化发生在代表地球（或地球平均形状）的球体表面上。

然而，真实的地球形状更接近椭球体而不是球体，北（或南）极的半径比赤道短约22公里（约6,356公里对比约6,378公里；）。在利用GRACE SH解提供的外部重力场变化进行质量变化反演时，为了计算简便起见，质量源被假设位于球体表面上。在这种情况下，球体上的质量变化与外部重力场之间存在一对一的关系，根据外部重力场和球体表面质量的SH表达式（在2-D假设下；参见Wahr et al.，1998）。然而，由于椭球体更好地表示地球的形状，质量变化应该在椭球体上进行分配，其中质量源到外部观测点的距离比球体情况下更大。以极地地区为例，为了在外部观测点上引起相同的重力场变化，椭球体上相应的质量变化应该比球体上的大（因为质量源到观测点的距离更长）。因此，根据球体地球模型假设（Wahr et al.，1998）常用的从GRACE SH解逆推质量变化的方法将导致偏差，因为真实的质量变化应该在球体内部的椭球体上。关于这个偏差，真实的质量变化应该比在球体地球假设下估计的要大。从现在起，将这个偏差称为椭球体修正。

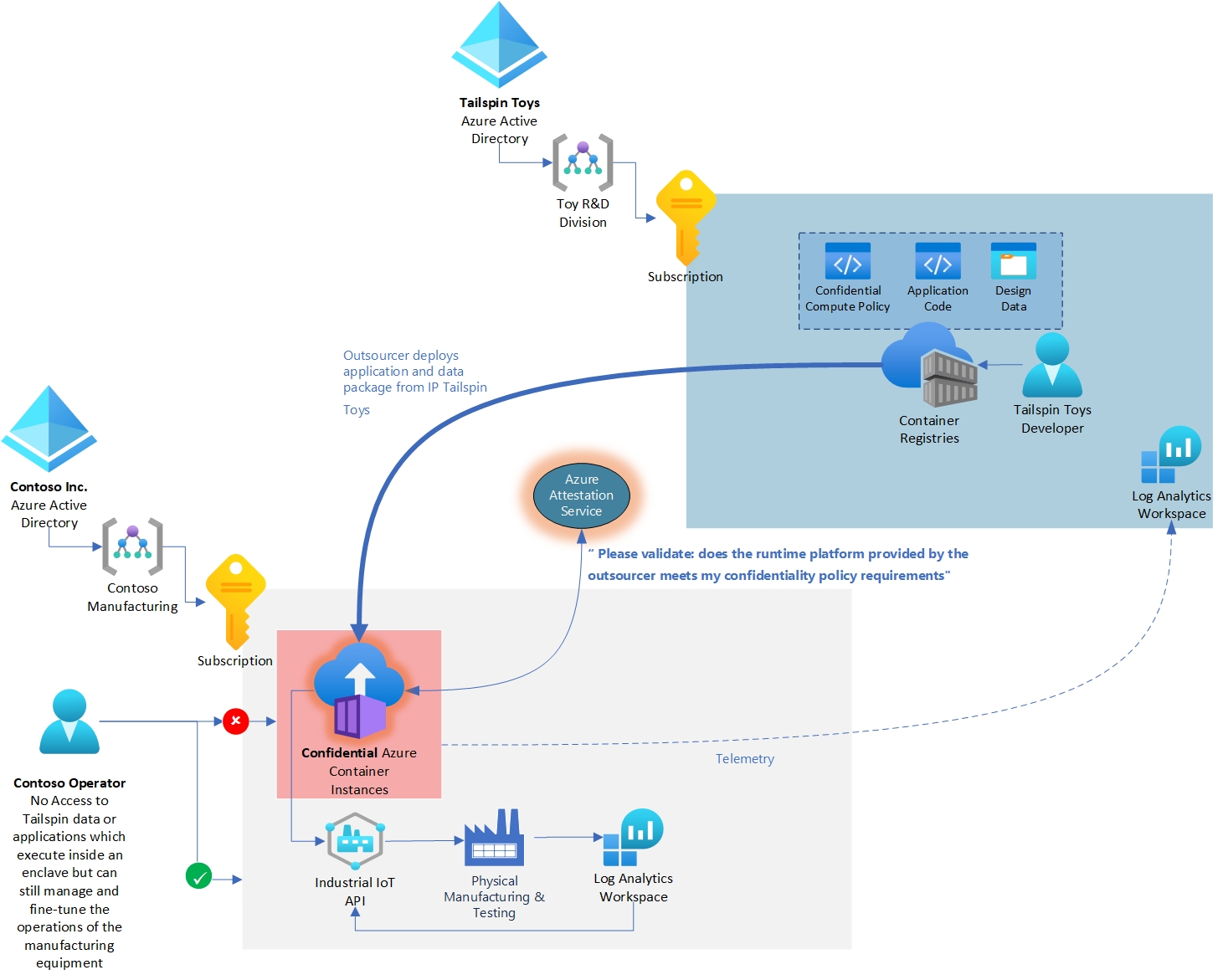
图片引用自 Li et al.(2017)

地球的形状比球体更接近椭球体。在质量变化反演中，通常使用球体近似会导致来自“重力恢复与气候实验”（GRACE）的球谐（SH）解产生偏差。

二、反演方法汇总

（1）经典的质量恢复原理可以在以下的文章中找到：

反演理论：正球体假设，2D质量分布假设

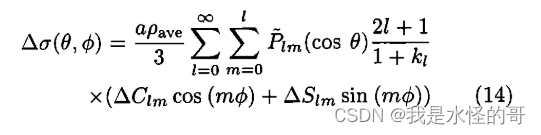
（2）加入椭球改正

文章提到椭球改正包括Li et al. (2017), Ditmar(2018)。

Li et al.(2017)文章摘要

地球的形状比球体更接近椭球体。在质量变化反演中通常采用的球体近似会导致来自“重力恢复与气候实验”（GRACE）的球谐（SH）解产生偏差，特别是在目前冰川损失显著的高纬度地区。根据基于合成质量变化率模型的模拟评估，这种偏差，或者说椭球体修正，可能高达8%。进一步评估使用了14多年的GRACE月度SH解（从2002年4月至2016年12月），表明椭球体修正在极地地区的总质量变化时间序列中也是显著的。在进行椭球体修正前后，来自质量变化时间序列的估计线性速率在格陵兰、南极半岛、阿蒙森海湾、阿拉斯加冰川和斯瓦尔巴群岛等五个选择区域上分别相差4.3%、4.7%、5.2%、5.7%和6.6%。尽管这些差异的振幅可能低于当前GRACE的不确定性水平，但这些差异在这五个地区都是一致的负值。这表明球体近似会导致对极地质量变化速率的系统低估。因此，对于使用GRACE SH解进行更精确的质量恢复，需要考虑椭球体修正。这也取决于质量变化信号的空间尺度（空间尺度越小，修正越大）。为了更可靠地估计GRACE SH解中的高纬度地表质量变化，推荐使用椭球体修正，特别是针对极地地区的冰损信号。

Ditmar(2018)文章摘要

GRACE卫星数据估计的时间变化Stokes系数通常被转换成地球表面的质量异常，使用了由Wahr等人（J Geophys Res 103(B12):30,205–30,229, 1998）提出的相应表达式。然而，用该表达式得到的结果代表了半径为6378公里的球体表面上的质量传输。我们发现，这种转换的准确性可能是不足的，特别是当目标区域位于极地地区且信噪比较高时。例如，在这种方式下，估计在2003年至2015年间格陵兰和西南极地区的Amundsen海湾上的平均线性趋势的峰值可能被低估约15%。作为解决方案，我们提出了一个更新的Stokes系数转换成质量异常的表达式。该表达式基于以下假设：（i）质量传输发生在参考椭球体上，（ii）在每个感兴趣点上，椭球面近似为球体，其半径等于该点到地球中心的当前径向距离（“局部球面近似”）。这个更新的表达式几乎和传统使用的表达式一样简单，但将转换过程的不准确性降低了一个数量级。另外，我们提醒读者，转换表达式是在球面（地心）坐标中定义的。我们展示了在球面和椭球面（大地测量）坐标之间计算质量异常的差异可能是不可忽视的，因此不能忽略将大地纬度转换为地心纬度。

其中Ditmar方法被CSR mascon数据处理采用，注意：用球谐系数进行质量反演，采用Whar et al.(1998)的方法，如果不进行椭球改正，在高纬度地区得到的结果会与mascon差异较大。下图是CSR mascon官网的备注。

Ditmar（2018）还提供了一个加入椭球改正的反演公式（可以替换Whar et al.(1998)的公式）

（3）加入地形改正

涉及的文章是Yang et al.(2022),其文章的摘要

传统上，将重力Stokes系数转换为地表质量，例如在GRACE（-FO）应用中，假定地球为一个完美的球体，这显然与实际情况不符。最近的研究通过考虑地球的扁率（椭球性）来纠正这种转换。然而，由于地形的存在，地球的几何形状要复杂得多，因此既不是一个球体也不是一个完美的椭球体。最近的研究以及本文的研究结果表明，将地球形状近似为一个假定的球体等几何近似将不可避免地导致来自GRACE重力场的地表质量估计中的偏差，从而可能对极地地区或山区的地球物理信号造成错误解读。

在这种情况下，我们提出了一种迭代缩放因子方法，通过考虑更真实的地球几何形状，包括其扁率、地形和大地面起伏，来实现更准确的地表质量估计。通过一系列模拟验证，我们发现所提出的方法高效（不超过四次迭代）、可靠（经过广泛的测试）和普遍准确（至少减少80%的偏差）。

相对于我们的方法，在理想球体地球假设下，从GRACE估计的2002年至2015年的平均线性趋势在格陵兰和西南极地区被发现被低估了约3.1%和5.5%，其中与地形有关的贡献分别为-0.5%（0.79 Gt/yr，负号表示高估）和-0.4%（0.34 Gt/yr）。尽管这个值很小，但它是一个值得考虑的系统偏差，例如，它大于通过将大气去混叠产品从RL05切换到RL06对西南极地区趋势估计的影响（0.3 Gt/yr）。此外，由地形引起的偏差在喜马拉雅山区迅速增加到2.7%（0.26mm/yr），甚至比椭球体引起的偏差（0.19mm/yr）还要大。

根据迄今为止的结果，地形引起的偏差被发现大约比GRACE目前的测量误差小一个数量级；然而，一旦GRACE朝着基准准确度的改进，这个偏差将变得相关。特别是，对于预期在前所未有的准确度和空间分辨率上绘制地球重力场的下一代地球重力模型（NGGM），应考虑地形修正。

Yang et al.(2022)的方法路线图

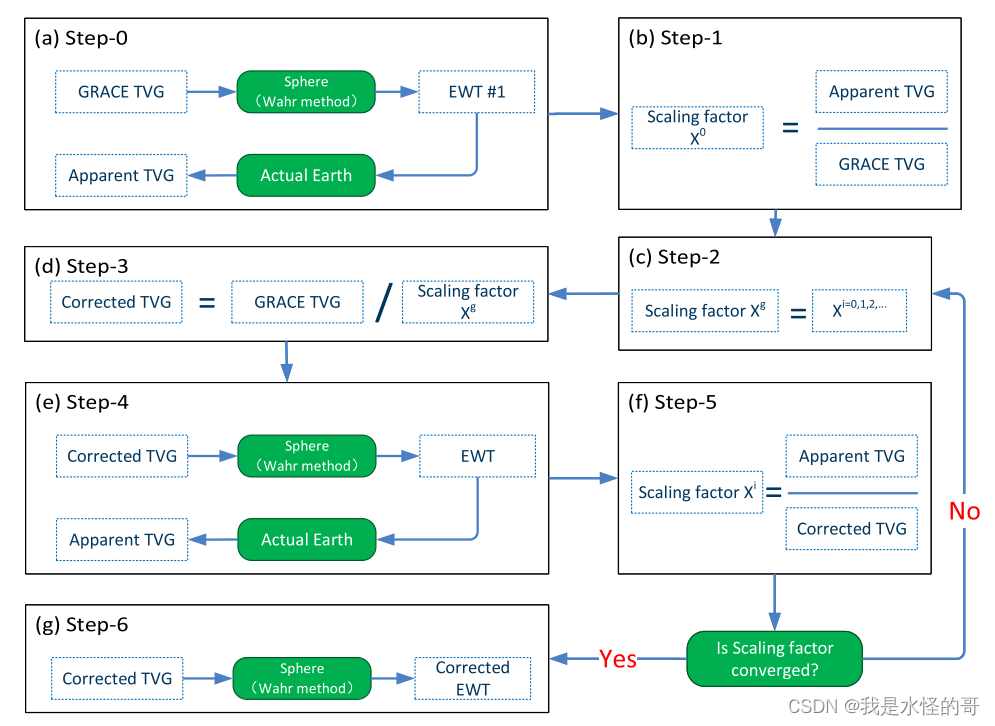
图片引自Yang et al.(2022)

而且文章还提供了python的程序，可以复现文章的结果：https://doi.org/10.6084/m9.figshare.17072969.

代码：

"""
@Company: CGE-HUST, Wuhan, China
@Author: Yang Fan
@Contact: yfan_cge@hust.edu.cn
@Modify Time:2021/11/23
@Description:
"""
import sys

sys.path.append('../')

from pysrc.LoadSH import LoadGsmByYear
from pysrc.LowDeg import LowDegreeReplace
from pysrc.Filtering import Gaussion
from pysrc.GC import GeometricalCorrection
from pysrc.Setting import FieldType, Assumption, LoveNumberType, EllipsoidType, SynthesisType
import numpy as np


def demo_GRACE_OneMonth():
    """
    This is a demo for GRACE ellipsoid/topography correction with our iterative scaling method.
    A demo for only one month's data processing.
    :return:
    """

    '''define the max degree of gravity solution'''
    lmax = 60
    '''Load the monthly gravity fields'''
    ts = LoadGsmByYear(localDir='../data/L2_SH_products/CSR', begin='2002', end='2020', opt='60')
    '''Preparation for the replacement of degree 1 and degree 2'''
    ld = LowDegreeReplace().load('../data/LowDegreeReplace')
    '''get the time-mean and replace degree 1/2'''
    C_mean = np.zeros(int((lmax + 2) * (lmax + 1) / 2))
    S_mean = np.zeros(int((lmax + 2) * (lmax + 1) / 2))
    for x in ts:
        '''low degree replacement'''
        ld.setGrav(x).rmDegZero().rpDegOne().rpDegTwo().rpDegThree()
        '''get the time-mean SHs'''
        C, S = x.getCS(lmax)
        C_mean += C
        S_mean += S
    C_mean = C_mean / len(ts)
    S_mean = S_mean / len(ts)

    '''remove the mean from monthly gravity fields'''
    SHC = [x.getCS(lmax)[0] - C_mean for x in ts]
    SHS = [x.getCS(lmax)[1] - S_mean for x in ts]

    '''specify one month's data as the input: the 35th monthly gravity field'''
    '''it could be an arbitrary one other than '35'.'''
    GivenMonth = 35
    print('\nStart the ellipsoid and topography correction for Month: %s to %s'
          % (ts[GivenMonth].date_begin, ts[GivenMonth].date_end))
    input = [SHC[GivenMonth], SHS[GivenMonth]]

    '''Gauss filter'''
    Gs = Gaussion().setRadius(300, lmax)
    input[0], input[1] = Gs.setCS(input[0], input[1]).getCS()

    '''define the griding type'''
    lat = np.arange(90, -90.1, -0.5)
    lon = np.arange(0, 360, 0.5)

    '''using the iterative scaling method to undertake the ellipsoid/topography correction'''
    gc = GeometricalCorrection().configure(Nmax=lmax, lat=lat, lon=lon,
                                           assumption=Assumption.ActualEarth, kind=FieldType.EWH)

    '''obtain the corrected gravity fields in terms of spherical harmonic coefficients'''
    output = gc.setInput(GravityField=input).correct()  
    
    '''Optionally, John Wahr's formulation can be applied to the output above to derive the correct surface mass'''
    '''load the pre-computed result, to check if the code works well'''
    validation = np.load('Output_verified.npy')
    return output, validation
    '''make a validation'''
    if np.max(output-validation) == 0.0:
        print('\nThe code is correctly configured')
    pass
    
if __name__ == '__main__':
    A,B =  demo_GRACE_OneMonth()

参考资料

Wahr J, Molenaar M, Bryan F (1998) Time variability of the Earth’s gravity field: hydrological and oceanic effects and their possible detection using GRACE. J Geophys Res Solid Earth 103(B12):30205–30229. https://doi.org/10.1029/98JB02844

Li J, Chen J, Li Z, Wang S-Y, Hu X (2017) Ellipsoidal correction in GRACE surface mass change estimation. J Geophys Res Solid Earth 122(11):9437–9460. https://doi.org/10.1002/ 2017JB014033

Ditmar P (2018) Conversion of time-varying Stokes coefficients into mass anomalies at the Earth’s surface considering the Earth’s oblateness. J Geodesy 92:1401–1412. https://doi.org/10.1007/ s00190-018-1128-0

Yang, F., et al. (2022). "On study of the Earth topography correction for the GRACE surface mass estimation." Journal of Geodesy 96(12).

感谢ChatGPT对翻译的大力支持：https://openai.com/blog/chatgpt