0 前面几种数据结构的回顾

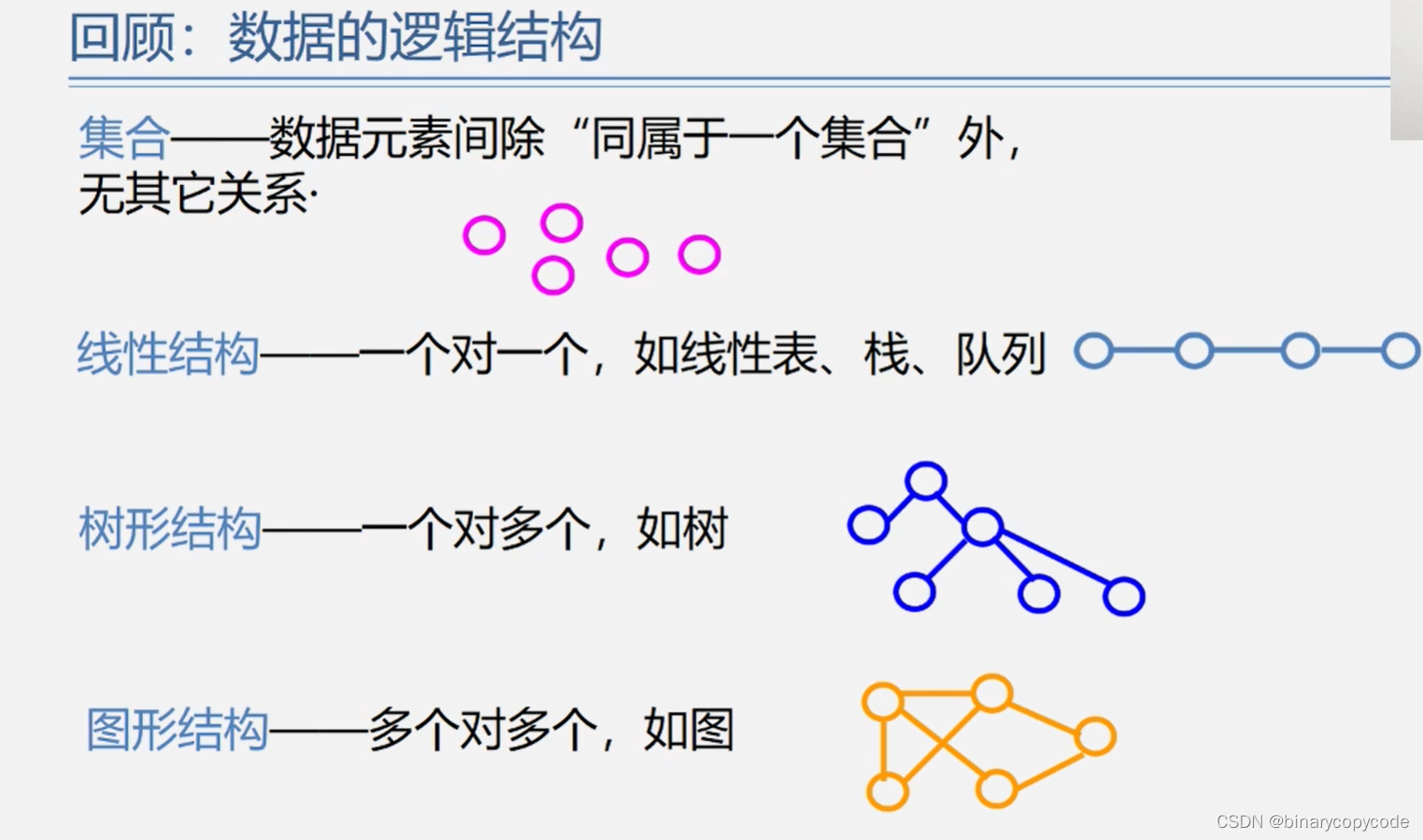
在这里插入图片描述

1 图

1.1 图的定义

图：
G = (V,E) // Graph = (Vertex, Edge)
V：顶点（Vertex）（数据元素）的有穷非空集合
E：边（Edege）的有穷集合在这里插入图片描述

1.2 常见术语

无向图：每条边都是无方向的（G2）
有向图：每条边都是有方向的（G1）
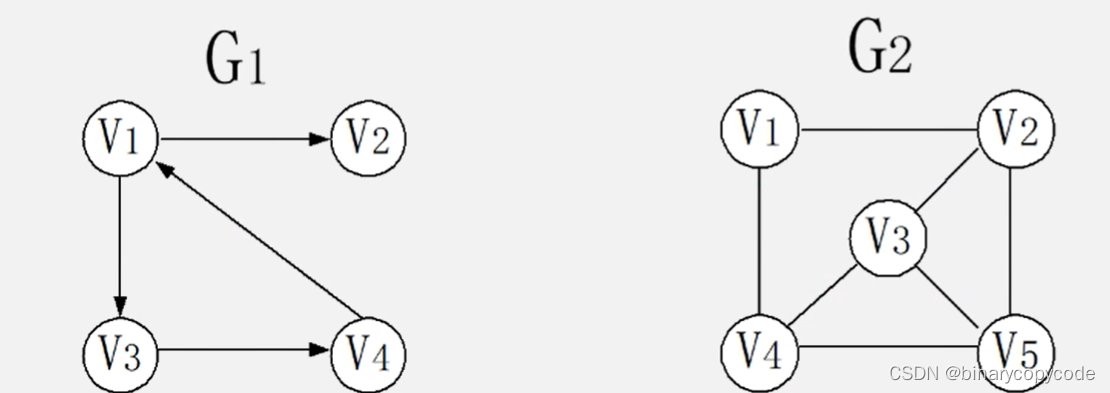
完全图：任意两个点都有一条边相连
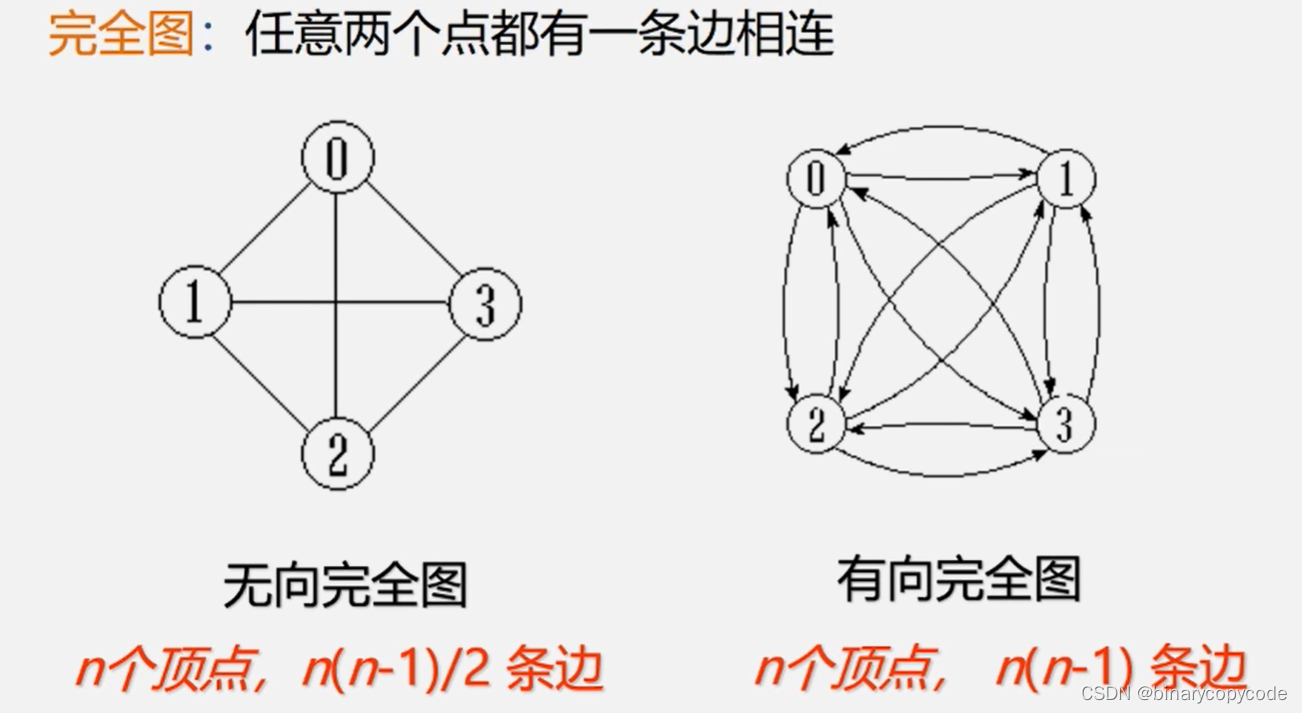
稀疏图：又很少边或弧的图（ $e < n l nn$ ）
稠密图：有较多边或弧的图
网：边/弧带权的图
邻接：有边/弧相连的两个顶点之间的关系，存在 $v_i,v_j)$ ，则称 $v_i$ 和 $v_j$ 互为邻接点，存在 $v_i,v_j>$ ，则称 $v_i$ 邻接到 $v_j$ ， $v_j$ 邻接与 $v_i$ 。用圆括号表示没有先后关系，用尖括号表示有先后关系，代指有向图与无向图
关联（依附）：边/弧与顶点之间的关系，存在 $v_i,v_j)$ / $v_i,v_j>$ ，则称该边/弧关联于 $v_i$ 和 $v_j$
顶点的度：与该顶点相关联的边的数目，记为TD(v)，在有向图中，顶点的度等于该顶点的入度与出度之和。顶点V的入度是以V为终点的有向边的条数，记作ID(v)；顶点V的出度是以V为始点的有向边的条数，记作OD(v)

Test：

在这里插入图片描述

1.3 图的抽象数据类型定义

在这里插入图片描述

1.4 表示一个图

1.4.1 邻接矩阵表示法

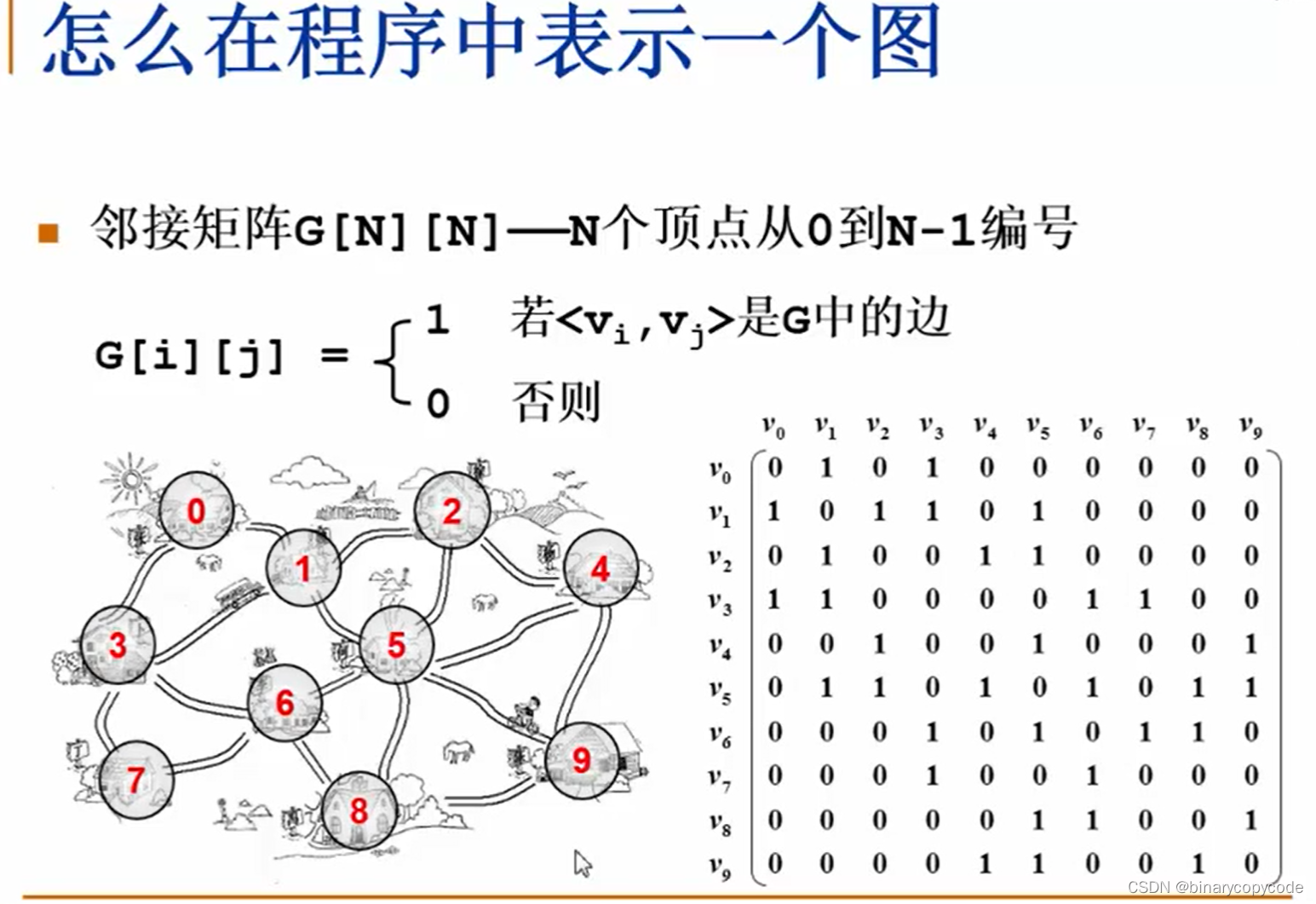
在这里插入图片描述

注意：有向图的邻接矩阵不一定是不对称的。

几个特点：

对角线都为0
矩阵是对称的，以对角线为轴，两边对称（举个例子：0和3两个点，0到3有一条边，相应的3到0也会有一条边）

问题：那么现在知道图是对称的一种结构，怎么在对于无向图的存储，可以节省一半的空间？
答：只存一半的元素。
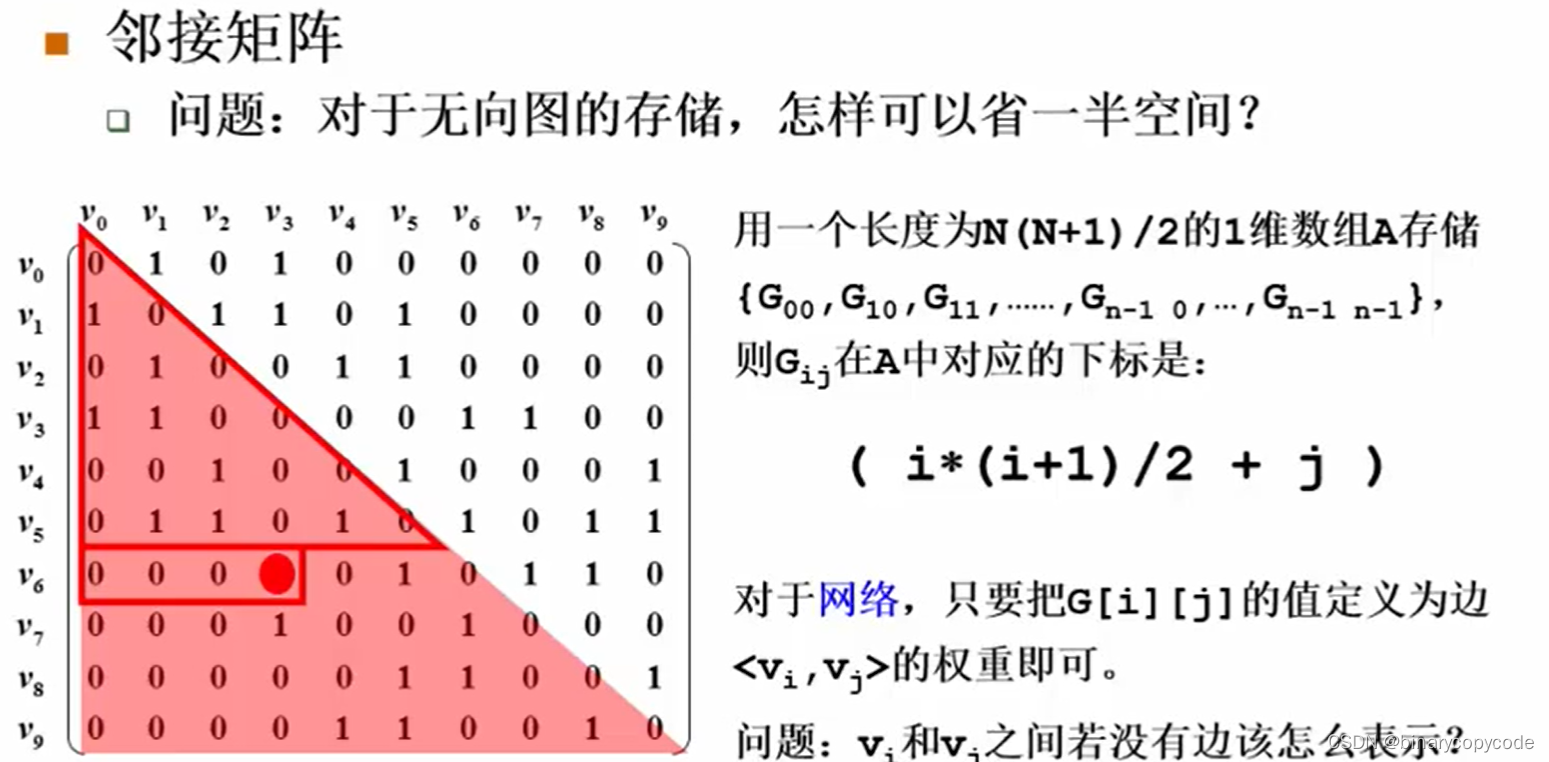
在这里插入图片描述
Test：

套用上方的公式 $(i * (i + 1) /2 + j)$ ，可以得出 $G_{20}$ 为 $G_{3}$ ，值为1，所以是有边的。

邻接矩阵的好处
在这里插入图片描述
Test：

出度看对应行元素，入度看对应列元素。

邻接矩阵的缺点
在这里插入图片描述

1.4.2 邻接表

将G[N]定义为指针数组（每个节点V一个指针），对应矩阵每行一个链表，只存非0元素。
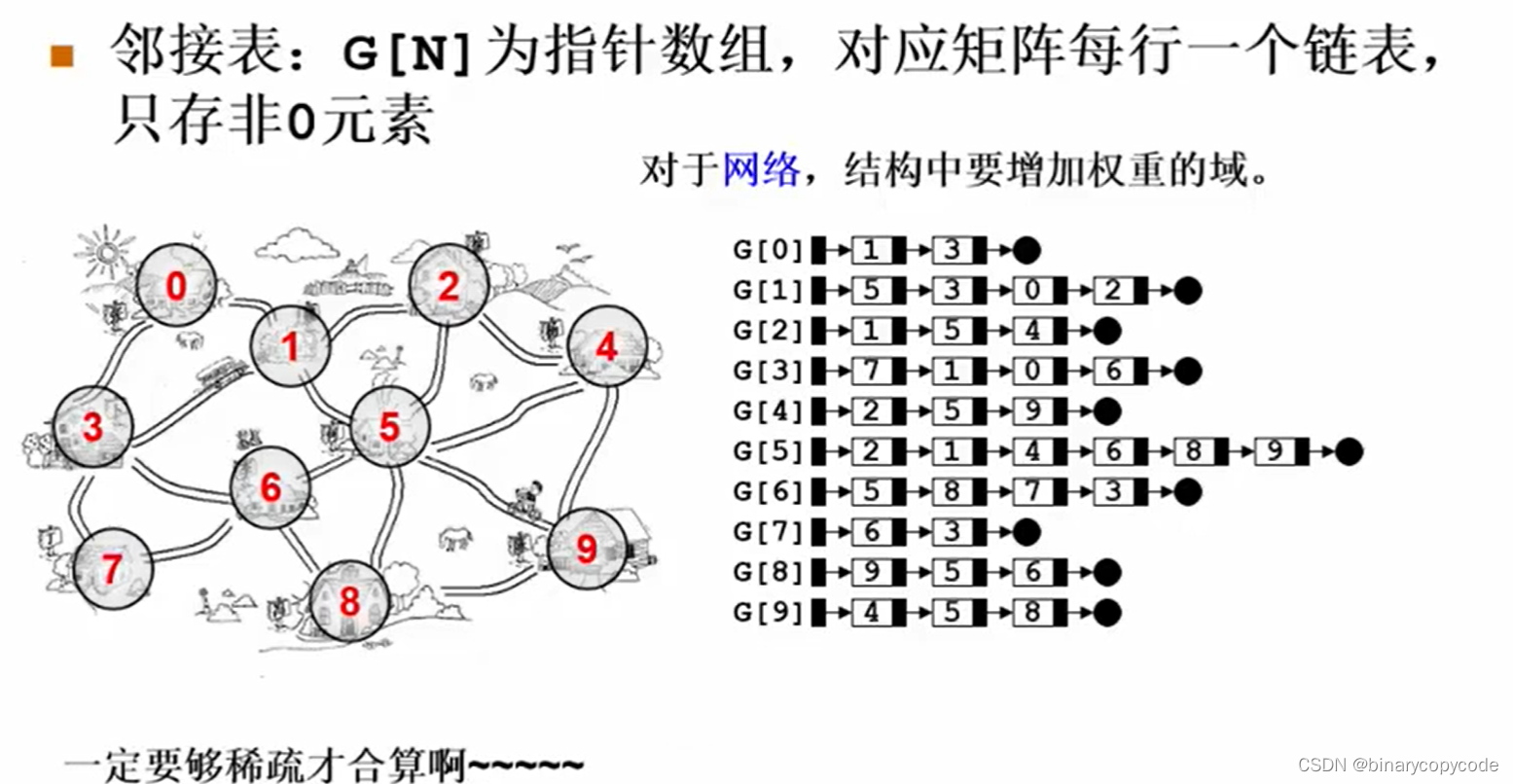
在这里插入图片描述

Test：
遍历整个邻接表的时间复杂度为？（假设N个顶点，E条边的图）
答：为 $O (N + E)$ 。

1.5 图的构建

1.5.1 邻接矩阵法

/* 图的邻接矩阵表示法 */

#define MaxVertexNum 100    /* 最大顶点数设为100 */
#define INFINITY 65535        /* ∞设为双字节无符号整数的最大值65535*/
typedef int Vertex;         /* 用顶点下标表示顶点,为整型 */
typedef int WeightType;        /* 边的权值设为整型 */
typedef char DataType;        /* 顶点存储的数据类型设为字符型 */

/* 边的定义 */
typedef struct ENode *PtrToENode;
struct ENode{
    Vertex V1, V2;      /* 有向边<V1, V2> */
    WeightType Weight;  /* 权重 */
};
typedef PtrToENode Edge;
       
/* 图结点的定义 */
typedef struct GNode *PtrToGNode;
struct GNode{
    int Nv;  /* 顶点数 */
    int Ne;  /* 边数   */
    WeightType G[MaxVertexNum][MaxVertexNum]; /* 邻接矩阵 */
    DataType Data[MaxVertexNum];      /* 存顶点的数据 */
    /* 注意：很多情况下，顶点无数据，此时Data[]可以不用出现 */
};
typedef PtrToGNode MGraph; /* 以邻接矩阵存储的图类型 */



MGraph CreateGraph( int VertexNum )
{ /* 初始化一个有VertexNum个顶点但没有边的图 */
    Vertex V, W;
    MGraph Graph;
    
    Graph = (MGraph)malloc(sizeof(struct GNode)); /* 建立图 */
    Graph->Nv = VertexNum;
    Graph->Ne = 0;
    /* 初始化邻接矩阵 */
    /* 注意：这里默认顶点编号从0开始，到(Graph->Nv - 1) */
    for (V=0; V<Graph->Nv; V++)
        for (W=0; W<Graph->Nv; W++)  
            Graph->G[V][W] = INFINITY;
            
    return Graph; 
}
       
void InsertEdge( MGraph Graph, Edge E )
{
     /* 插入边 <V1, V2> */
     Graph->G[E->V1][E->V2] = E->Weight;    
     /* 若是无向图，还要插入边<V2, V1> */
     Graph->G[E->V2][E->V1] = E->Weight;
}

MGraph BuildGraph()
{
    MGraph Graph;
    Edge E;
    Vertex V;
    int Nv, i;
    
    scanf("%d", &Nv);   /* 读入顶点个数 */
    Graph = CreateGraph(Nv); /* 初始化有Nv个顶点但没有边的图 */ 
    
    scanf("%d", &(Graph->Ne));   /* 读入边数 */
    if ( Graph->Ne != 0 ) { /* 如果有边 */ 
        E = (Edge)malloc(sizeof(struct ENode)); /* 建立边结点 */ 
        /* 读入边，格式为"起点 终点 权重"，插入邻接矩阵 */
        for (i=0; i<Graph->Ne; i++) {
            scanf("%d %d %d", &E->V1, &E->V2, &E->Weight); 
            /* 注意：如果权重不是整型，Weight的读入格式要改 */
            InsertEdge( Graph, E );
        }
    } 

    /* 如果顶点有数据的话，读入数据 */
    for (V=0; V<Graph->Nv; V++) 
        scanf(" %c", &(Graph->Data[V]));

    return Graph;
}

1.5.2 邻接表法

/* 图的邻接表表示法 */

#define MaxVertexNum 100    /* 最大顶点数设为100 */
typedef int Vertex;         /* 用顶点下标表示顶点,为整型 */
typedef int WeightType;        /* 边的权值设为整型 */
typedef char DataType;        /* 顶点存储的数据类型设为字符型 */

/* 边的定义 */
typedef struct ENode *PtrToENode;
struct ENode{
    Vertex V1, V2;      /* 有向边<V1, V2> */
    WeightType Weight;  /* 权重 */
};
typedef PtrToENode Edge;

/* 邻接点的定义 */
typedef struct AdjVNode *PtrToAdjVNode; 
struct AdjVNode{
    Vertex AdjV;        /* 邻接点下标 */
    WeightType Weight;  /* 边权重 */
    PtrToAdjVNode Next;    /* 指向下一个邻接点的指针 */
};

/* 顶点表头结点的定义 */
typedef struct Vnode{
    PtrToAdjVNode FirstEdge;/* 边表头指针 */
    DataType Data;            /* 存顶点的数据 */
    /* 注意：很多情况下，顶点无数据，此时Data可以不用出现 */
} AdjList[MaxVertexNum];    /* AdjList是邻接表类型 */

/* 图结点的定义 */
typedef struct GNode *PtrToGNode;
struct GNode{  
    int Nv;     /* 顶点数 */
    int Ne;     /* 边数   */
    AdjList G;  /* 邻接表 */
};
typedef PtrToGNode LGraph; /* 以邻接表方式存储的图类型 */



LGraph CreateGraph( int VertexNum )
{ /* 初始化一个有VertexNum个顶点但没有边的图 */
    Vertex V;
    LGraph Graph;
    
    Graph = (LGraph)malloc( sizeof(struct GNode) ); /* 建立图 */
    Graph->Nv = VertexNum;
    Graph->Ne = 0;
    /* 初始化邻接表头指针 */
    /* 注意：这里默认顶点编号从0开始，到(Graph->Nv - 1) */
       for (V=0; V<Graph->Nv; V++)
        Graph->G[V].FirstEdge = NULL;
            
    return Graph; 
}
       
void InsertEdge( LGraph Graph, Edge E )
{
    PtrToAdjVNode NewNode;
    
    /* 插入边 <V1, V2> */
    /* 为V2建立新的邻接点 */
    NewNode = (PtrToAdjVNode)malloc(sizeof(struct AdjVNode));
    NewNode->AdjV = E->V2;
    NewNode->Weight = E->Weight;
    /* 将V2插入V1的表头 */
    NewNode->Next = Graph->G[E->V1].FirstEdge;
    Graph->G[E->V1].FirstEdge = NewNode;
        
    /* 若是无向图，还要插入边 <V2, V1> */
    /* 为V1建立新的邻接点 */
    NewNode = (PtrToAdjVNode)malloc(sizeof(struct AdjVNode));
    NewNode->AdjV = E->V1;
    NewNode->Weight = E->Weight;
    /* 将V1插入V2的表头 */
    NewNode->Next = Graph->G[E->V2].FirstEdge;
    Graph->G[E->V2].FirstEdge = NewNode;
}

LGraph BuildGraph()
{
    LGraph Graph;
    Edge E;
    Vertex V;
    int Nv, i;
    
    scanf("%d", &Nv);   /* 读入顶点个数 */
    Graph = CreateGraph(Nv); /* 初始化有Nv个顶点但没有边的图 */ 
    
    scanf("%d", &(Graph->Ne));   /* 读入边数 */
    if ( Graph->Ne != 0 ) { /* 如果有边 */ 
        E = (Edge)malloc( sizeof(struct ENode) ); /* 建立边结点 */ 
        /* 读入边，格式为"起点 终点 权重"，插入邻接矩阵 */
        for (i=0; i<Graph->Ne; i++) {
            scanf("%d %d %d", &E->V1, &E->V2, &E->Weight); 
            /* 注意：如果权重不是整型，Weight的读入格式要改 */
            InsertEdge( Graph, E );
        }
    } 

    /* 如果顶点有数据的话，读入数据 */
    for (V=0; V<Graph->Nv; V++) 
        scanf(" %c", &(Graph->G[V].Data));

    return Graph;
}