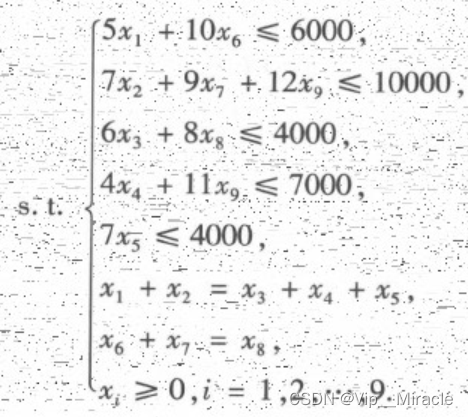一.题干

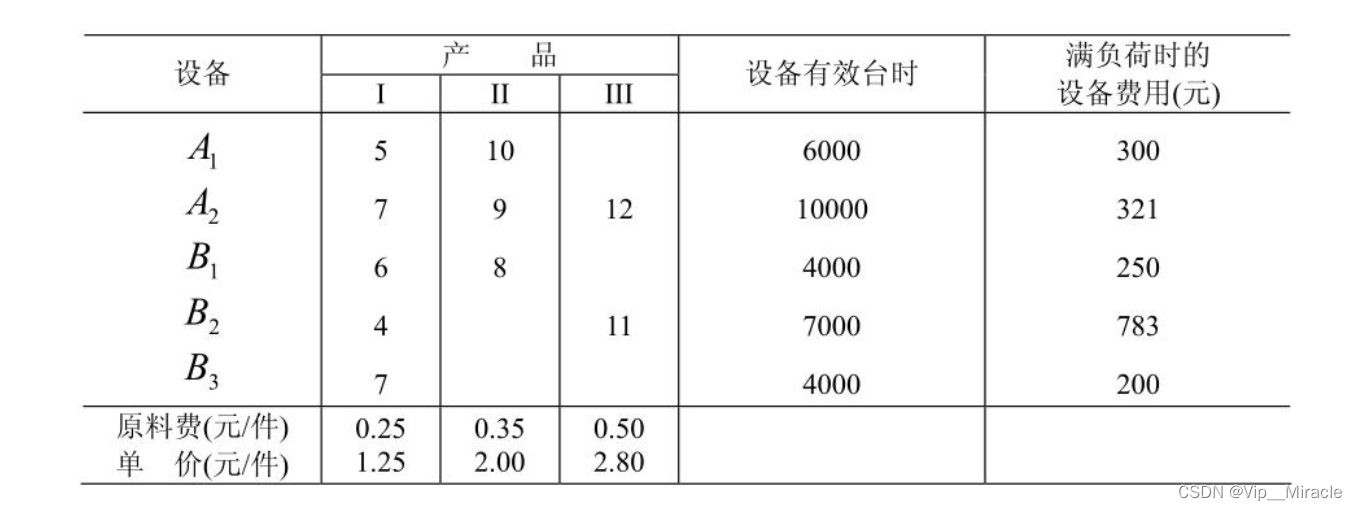
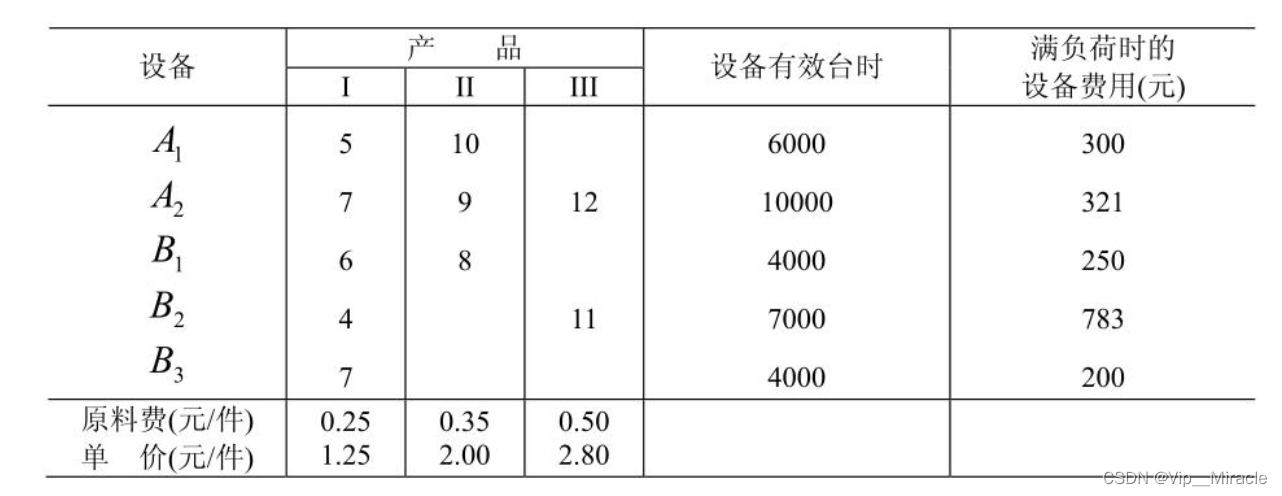
某厂生产三种产品 I， II， III。 每种产品要经过 A、 B两道工序加工。 设该厂有两种规格的设备能完成 A 工序， 它们以A1、 A2表示； 有三种规格的设备能完成 B 工序， 它们以B1、 B2、 B3表示。 产品 I 可在 A、 B任何一种规格设备上加工。 产品 II 可在任何规格的 A 设备上加工， 但完成 B 工序时， 只能在B1设备上加工； 产品 III 只能在A2与B2设备上加工。 已知在各种机床设备的单件工时， 原材料费， 产品销售价格， 各种设备有效台时以及满负荷操作时机床设备的费用如表 2， 求安排最优的生产计划， 使该厂利润最大。

二.解答

2.1 先读懂题干

1.表格中“产品”下的数字是什么意思？
解答：以第Ⅰ类产品为例，看那一列。意思就是第Ⅰ种产品，经过A道工序中的A1设备，所需要花费5小时（单位可以理解为小时）生产一件；如果经过A2设备，所需要花费7小时生产一件；经过B道工序时，如果走B1设备需要花费6小时生产一件，如果走B2设备需要花费4小时生产一件，如果走B3设备则需花费7小时生产一件；
其余的以此类推…

2.设备有效台时是什么意思?
解答：每个设备正常工作时长的最大值，比如说A1，他只能满负荷工作6000小时，否则机器就炸了，你可以这么理解…

3.满负荷时设备的设备费用是什么意思？
解答：通俗的说就是工作6000个小时所要花费的机器损耗是300元，300/6000就是每小时机器磨损的花费；
剩下几个也是这个意思…

2.2 解体思路

对产品Ⅰ来说，设经过A道工序中的设备A1、A2所生产的产品数是x1、x2件，设经过B道工序中的B1,B2,B3所生产的产品数是x3,x4,x5件；

对产品Ⅱ来说，设经过A道工序中的设备A1、A2所生产的产品数是x6、x7件，设经过B道工序中的设备B1所生产的产品数是x8件；

对产品Ⅲ来说，设经过A道工序中的设备A2所生产的产品数是x9件，设经过B到工序中设备B2的产品件数也是x9件（注意：这里不是写错了，是故意这么写的，因为经过A2设备的产品数必定是经过是经过B2设备的产品数，因为是同一批产品呀，只不过需要经过不同的两个环节加工而已！）
根据以上分析，有：

产品Ⅰ的数量 ：x1 + x2 = x3 +x4 +x5
产品Ⅱ的数量 ：x6 + x7 = x8
产品Ⅲ的数量 ：x9 = x9

不知道大家伙上面的几个式子能不能看懂，因为不管是A道工序还是B道工序，都是同一个产品，只不过是先经过A道工序，再经过B道工序而已…

所以产品Ⅰ的数量：x1+x2或者是x3+x4+x5；
产品Ⅱ的数量 ：x6 + x7 或者是x8
产品Ⅲ的数量 ：x9

利润公式：
利润 = 挣的钱 - 成本
=（每件的售价 - 成本）×产品的数量 - 设备的工作时间 × 每小时的损耗的钱
对应于这道题是:
利润 = （单价 - 原料费）× 产品的数量 - 设备的工作时间 × 每小时的损耗钱

目标方程：

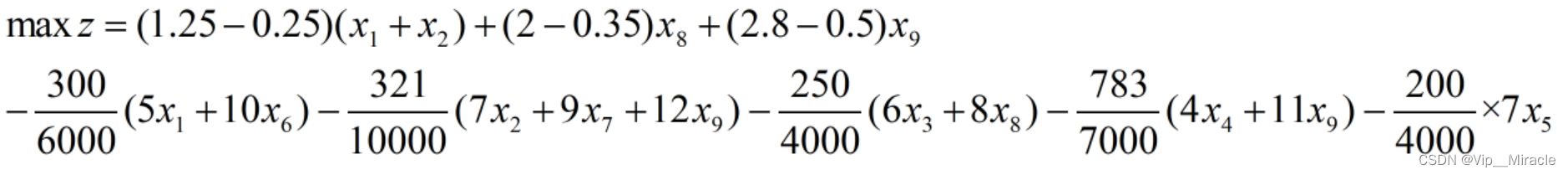
约束条件