hello,大家好,这里是bang___bang_,今天来记录2道习题跳石板和手套!

目录
1️⃣跳石板
2️⃣手套
1️⃣跳石板
跳石板_牛客题霸_牛客网 (nowcoder.com)
描述
小易来到了一条石板路前,每块石板上从1挨着编号为:1、2、3.......
这条石板路要根据特殊的规则才能前进:对于小易当前所在的编号为K的 石板,小易单次只能往前跳K的一个约数(不含1和K)步,即跳到K+X(X为K的一个非1和本身的约数)的位置。 小易当前处在编号为N的石板,他想跳到编号恰好为M的石板去,小易想知道最少需要跳跃几次可以到达。
例如:
N = 4,M = 24:
4->6->8->12->18->24
于是小易最少需要跳跃5次,就可以从4号石板跳到24号石板
输入描述:
输入为一行,有两个整数N,M,以空格隔开。 (4 ≤ N ≤ 100000) (N ≤ M ≤ 100000)
输出描述:
输出小易最少需要跳跃的步数,如果不能到达输出-1
示例:
输入:4 24
输出:5
解题思路:
多种解中找最优解,动态规划!分解规模!前面小规模的答案能被后面的问题利用!
从当前石板开始模拟跳跃,求解约数,跳约数距离至对应石板,更新为最小步数。
模拟跳跃过程:如果当前石板无法通过前一个石板跳到(标记INT_MAX,表示不可达),直接越过这个石板(continue)往后寻找前一个石板可以跳至的石板。前一个跳至的石板决定跳至当前石板的步数!
转移方程:
step[res[j]+i]=min(step[i]+1,step[res[j]+i]) //i为石板编号,res[j]为i的约数
step[n]=0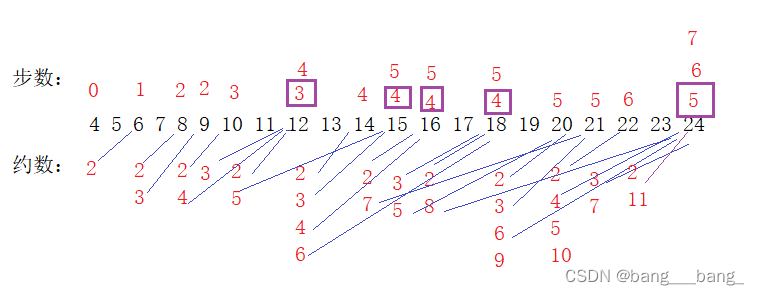 实现代码:
实现代码:
#include<iostream>
#include<limits.h>
#include<vector>
#include<cmath>
using namespace std;
void get_div_num(int n,vector<int>& res)
{
for(int i=2;i<=sqrt(n);i++)
{
if(n%i==0)
{
res.push_back(i);
if(n/i!=i)
{
res.push_back(n/i);
}
}
}
}
int Jump(int n,int m)
{
//存对应石板的跳跃步数
vector<int> step(m+1,INT_MAX);//下标从0开始多开1个保持和石板编号一一对应
step[n]=0;//开始石板不需要跳,值为0
//从编号为n的石板开始跳
for(int i=n;i<m;i++)
{
//如果当前石板存值为INT_MAX表示该石板跳不到
if(step[i]==INT_MAX)
{
continue;
}
//当前石板可到达,求解往后跳的约数
vector<int>res;
//获取约数
get_div_num(i,res);
for(int j=0;j<res.size();j++)
{
//之前已有跳跃数,更新挑选该石板的最少跳跃数
if(res[j]+i<=m&&step[res[j]+i]!=INT_MAX)
{
step[res[j]+i]=min(step[i]+1,step[res[j]+i]);
}
//之前没有跳跃数,跳跃数+1
else if(res[j]+i<=m)
{
step[res[j]+i]=step[i]+1;
}
}
}
return step[m]==INT_MAX?-1:step[m];
}
int main() {
int n,m,min_step;
while(cin>>n>>m)
{
min_step=Jump(n,m);
cout<<min_step<<endl;
}
return 0;
}
2️⃣手套
手套_牛客题霸_牛客网 (nowcoder.com)
描述
在地下室里放着n种颜色的手套,手套分左右手,但是每种颜色的左右手手套个数不一定相同。A先生现在要出门,所以他要去地下室选手套。但是昏暗的灯光让他无法分辨手套的颜色,只能分辨出左右手。所以他会多拿一些手套,然后选出一双颜色相同的左右手手套。现在的问题是,他至少要拿多少只手套(左手加右手),才能保证一定能选出一双颜色相同的手套。
给定颜色种数n(1≤n≤13),同时给定两个长度为n的数组left,right,分别代表每种颜色左右手手套的数量。数据保证左右的手套总数均不超过26,且一定存在至少一种合法方案。
测试样例:
4,[0,7,1,6],[1,5,0,6]
返回:10
解题思路:
这个题目说至少拿多少只手套,那我们要保证把没有颜色匹配的拿出来(即左边有,右边没有;或者左边没有,右边有)并且我们还要保证使一边手套的每种都拿出来至少一只(选出需要拿的数量最少的一边),然后再从另一边拿1只就可以得到至少拿的数量。
🌰[0,7,1,6] [1,5,0,6]
假设从左往右是:红 蓝 黄 绿 (方便我描述)
1.红和黄是颜色无法匹配的!先拿出来!(也就是0+1+1+0=2)
2.拿出无法匹配的后,其实变成了[7,6] [5,6]
3.使一边手套的每种至少都拿出来1只,也就是sum-min+1。
左边:7+6-6+1=8(最少拿8只才能保证每种都取了一只)
右边 :5+6-5+1=7(最少拿7只才能保证每种都取了一只)
4.选取小的一边右边(也就是7)
5.现在右边所有的种类都能保证取出1只,只需要再从左边取1只,即可。(也就是1)
6.最终取出的数量(2+min(8,7)+1=10)
代码实现:
class Gloves {
public:
int findMinimum(int n, vector<int> left, vector<int> right) {
int left_min=INT_MAX,right_min=INT_MAX;
int left_sum=0,right_sum=0;
int count=0;
for(int i=0;i<n;i++)
{
//有一边为0的
if(left[i]*right[i]==0)
{
count+=left[i]+right[i];
}
//sum-min+1
else {
left_min=left_min<left[i]?left_min:left[i];
left_sum+=left[i];
right_min=right_min<right[i]?right_min:right[i];
right_sum+=right[i];
}
}
return count+min(left_sum-left_min+1,right_sum-right_min+1)+1;
}
};文末结语,本文记录了1道动态规划题(跳石板),1道贪心(手套),如有需要,希望能有所帮助!