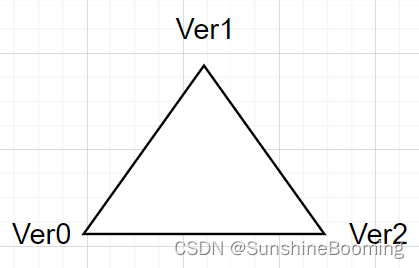
二叉树的构造(如何唯一确定一棵二叉树?附证明)
一些直观的认识
▪ 同一棵二叉树具有唯一先序序列、中序序列和后序序列。
▪ 不同的二叉树可能具有相同的先序序列、中序序列和后序序列。
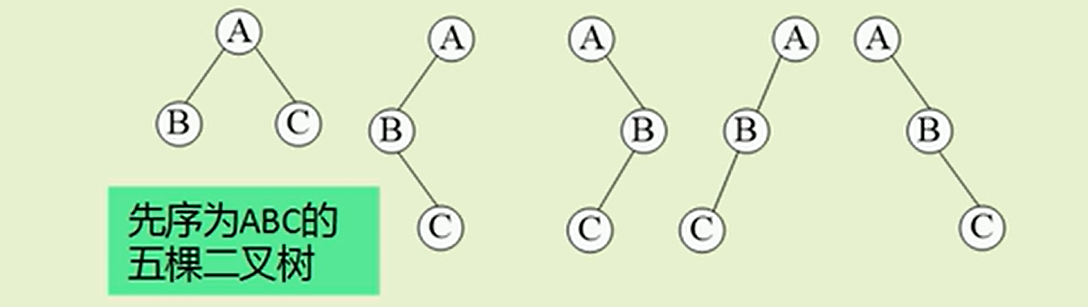
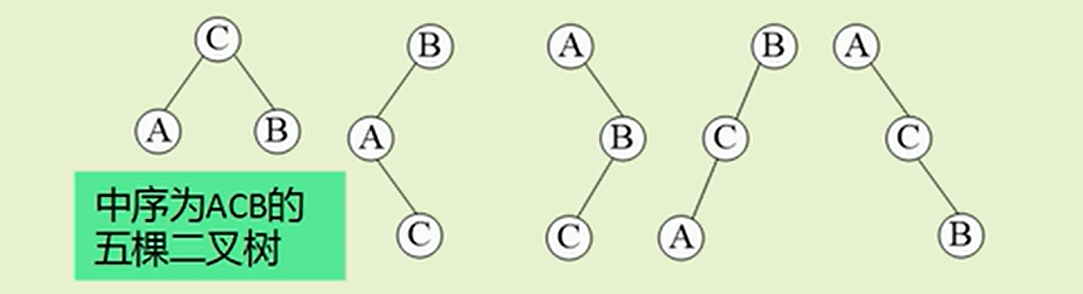
通过上面两个例子的验证:
▪ 仅有一个先序序列(或中序序列、后序序列),无法确定这颗二叉树的树形!
▪ 思考:给定先序序列、中序和后序遍历序列中任意两个,是否可以唯一确定这颗二叉树的树形?
二叉树的构造
(1) 同时给定一棵二叉树的先序序列和中序序列,就能唯一确定棵二叉树?
• 是!
• 定理1
(2) 同时给定一棵二叉树的中序序列和后序序列,就能唯一确定这棵二叉树?
• 是
• 定理2
(3) 同时给定一棵二叉树的先序序列和后序序列,就能唯一确定这棵二叉树吗?
• 否
下面我们给出证明:
定理1
▪ 任何n(n>=0)个不同节点的二叉树,都可由它的中序序列和先序序列唯一地确定。
证明(数学归纳法)
• 基础: 当 n=0 时,二叉树为空,结论正确.
• 假设: 设节点数小于n的任何二叉树,都可以由其先序序列和中序序列唯一地确定
• 归纳: 已知某二叉树具有n(n>0)个不同节点,其先序序列是a0a1 …an-1;中序序列是b0b1…bk-1bk+1…bn-1 .
▪ 先序遍历“根-左-右”,a0 必定是二叉树的根节点
▪ a0 必然在中序序列中出现,设在中序序列中必有某个bk(0<=k<=n-1)就是根节点a0。

• 由于bk是根节点,中序遍历“左-根-右”,故中序遍历中
▪ b0b1…bk-1必是根节点bk(a0)左子树的中序序列,即bk的左子树有k个节点
▪ bk+1…bn-1必是根节点bk(a0)右子树的中序序列,即bk的右子树有n-k-1个节点
• 对应先序序列,紧跟在根节点a0之后的k个节点a1…ak是左子树的先序序列,ak+1…an-1,这n-k-1就是右子树的先序序列.
• 根据归纳假设,子先序序列a1…ak和子序序列b0b1…bk-1可以唯一地确定根节点a0的左子树,而先序序列ak+1…an-1和子中序序列bk+1…bn-1可以唯一地确定根节点a0的右子树.
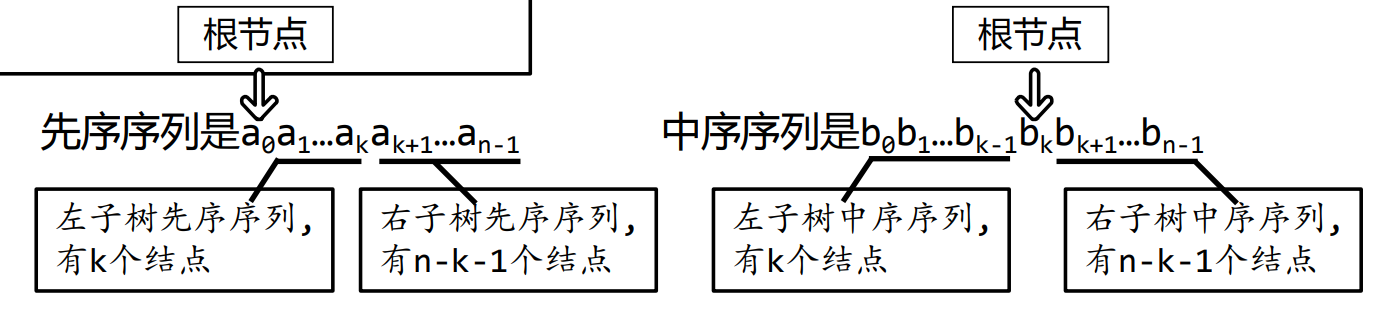
通过上面的证明,我们从先序遍历和中序遍历进行逐层分解,唯一确定了一个二叉树.进而逆向证明了二叉树是可以通过其先序遍历和中序遍历唯一确定.
我们观察下面例子:
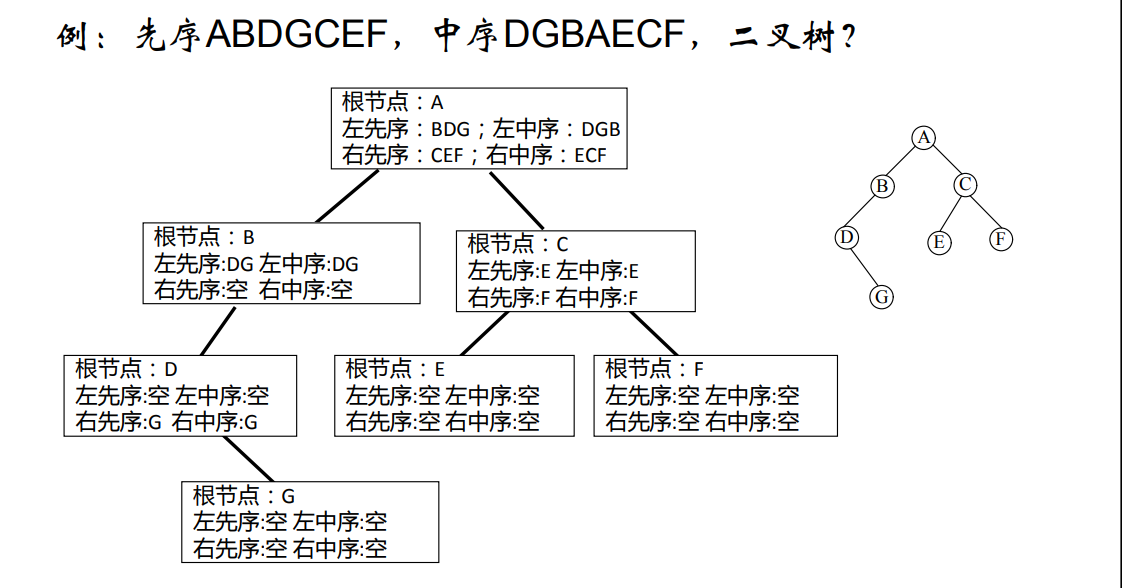
①通过先序遍历序列的第一个节点,即可确定二叉树的根。
②我们根据得到的根查找中序遍历序列,就可以找到此二叉树的根。
根据中序遍历的特点就可以得知:根节点的左边就是其左子树的中序遍历序列,其右边就是其右子树的中序遍历序列
③我们通过查找中序序列的根的左边的节点个数,就可以确定二叉树的左子树,根据根右边的节点个数,就可以确定二叉树的右子树。
④ 根据中序序列的第二个节点,就可以确定下一层级的根节点,然后拿这个根节点去查找中序遍历的序列,就可以找到此层级的左子树和右子树,以此类推。
所以我们可以根据上面证明的性质,进行二叉树的构造
算法实现
框架:
BTNode *CreateBT1(先序序列,中序序列,处理的本层级的二叉树节点个数)
{
如果传入的二叉树节点个数是0,则返回空;
否则,为新节点申请空间;
在先序序列第一个节点确定二叉树的根;
拿着根节点在中序序列找到根节点位置k;
然后我们拿着这个序列就可以确定本层级的根的左右子树,
就可以构造下一层级的二叉树了.
返回构造的二叉树即可;
}
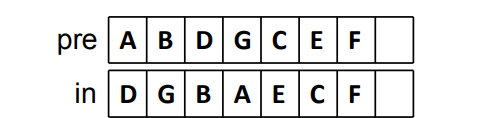
代码实现:
//传入先序序列,中序序列,本层级处理的二叉树节点个数
BTNode *CreateBT1(char *pre,char *in,int n)
{
//定义访问二叉树的指针
BTNode *s;
//定义寻找二叉树的根的中间变量
char *p;
//定义根节点的位置k
int k;
//先判断二叉树是否为空
if(n<=0)
{
return NULL;
}
//如果通过上述验证,则不为空,为根节点申请空间
s = (BTNode *)malloc(sizeof(BTNode));
//根节点数据区赋值,即为先序序列pre的第一个字符
s->data = *pre;
//现在根找到了,就去找二叉树的左右子树
//这就需要借助中序序列了,中序序列遍历顺序为左->根->右,所以先找到根,就可以找到其左子树
//在中序中找根节点的位置k
for(p=in;p<in+n;p++) //in是传入的in数组开始的位置
{
if(*p==*pre)
{
break;
}
}
//找到根节点的位置,我们就找到了此层级的二叉树的根,同时我们也就可以通过中序序列数组
//确定二叉树左子树的个数和右子树的个数, 为下一层级构造做准备
k = p-in; //根开始位置减去数组开始位置,就是左子树个数
//构造左右子树
s->lchild = CreateBT1(pre+1,in,k);
//pre+1:下一层级的左子树根,我们对先序序列指针后移一位
//in: 中序序列,左子树仍然是从头开始
//k : 左子树个数就是上面求的
s->rchild = CreateBT1(pre+k+1,p+1,n-k-1);
//右子树的根,我们既然已经知道左子树的个数,就知道根在先序序列第几位
//pre+k+1: 右子树的先序序列是根右边的,我们通过查个数即可知道其开始的位序=开始+左子树+1
//p+1: 右子树的中序序列是根右边开始的,所以从根的位置p+1即可
//n-k-1: 右子树的个数是总是减去左子树,再减去根
//最后返回构造的二叉树即可
return s;
}
定理2
▪ 任何n (n>0)个不同节点的二叉树,都可由它的中序序列和后序序列唯一地确定.
证明:
如下图:
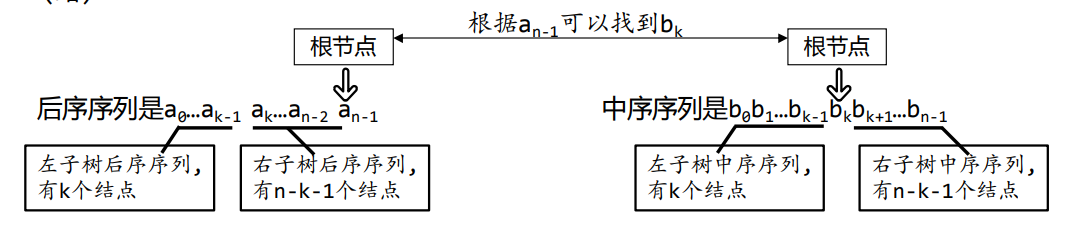
通过构造二叉树的先序序列和中序序列,后序序列,我们可以发现,每一步都是有条不紊的,每一步都是分层次的,我们通过构造序列的过程,逆向可以构造出二叉树,就间接地证明了,这个定义的合法性.
思维拓展:
为什么中序遍历和先序遍历
中序遍历和后序遍历可以唯一确定一棵二叉树
定时先序遍历和后序遍历就不能呢?
我们可以从同一层级的构造上面进行直观理解:
中序遍历是 : 左-根-右 ---->通过根, 就可以唯一确定本层次的左右子树的节点个数
先序遍历: 根-左-右 ----->根是必然是第一个, 不确定的就是左子树和右子数
后序遍历: 左-右-根 ----->根必然是最后一个节点,不确定的就是左子树和右子树
这样就理解了吧,我们下节ヾ( ̄▽ ̄)Bye>Bye!