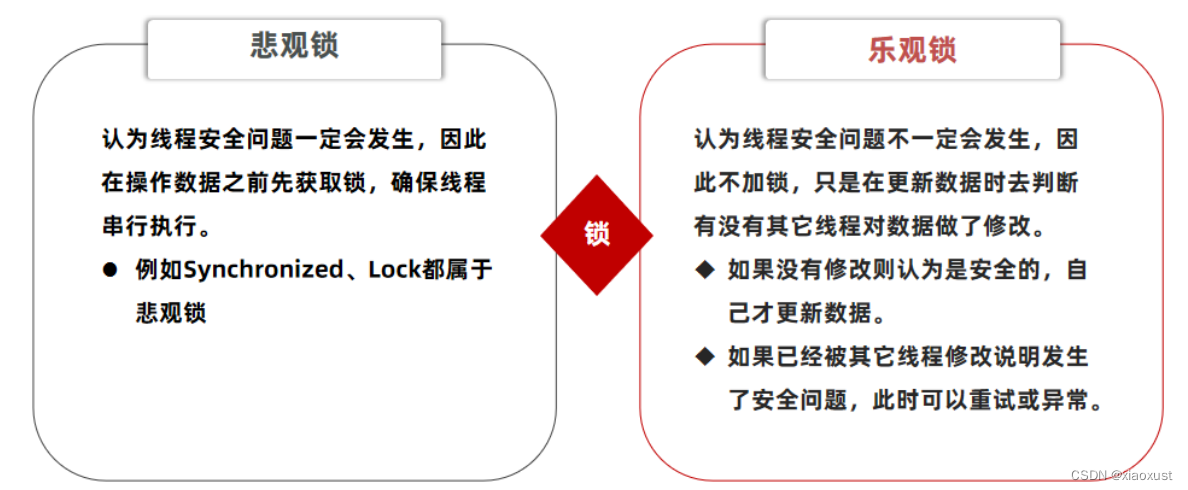
“”“单例模式”“”

“”“工厂模式”“”

class Person:
    pass


class Worker(Person):
    pass


class Student(Person):
    pass


class Teacher(Person):
    pass


class Factory:
    def get_person(self, p_type):
        if p_type == 'w':
            return Worker()
        elif p_type == 's':
            return Student()
        else:
            return Teacher()


pf = Factory()
worker = pf.get_person('w')
stu = pf.get_person('s')
teacher = pf.get_person('t')