💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
📚2 运行结果
🎉3 参考文献
🌈4 Matlab代码实现
💥1 概述
小波尺度谱是通过分段离散小波变换(Discrete Wavelet Transform, DWT)计算得到的一种信号分析方法。它可以帮助我们理解信号在不同尺度上的频率特性以及信号在时间与频率域上的变化情况。
下面是一种常见的计算小波尺度谱的方法:
1. 首先,选择一个合适的小波函数作为基函数。常用的小波函数包括Daubechies、Haar、Morlet等。
2. 将要进行分析的信号进行分段离散小波变换,将信号分解为不同尺度上的近似系数和细节系数。这个过程可以使用快速小波变换算法(Fast Wavelet Transform, FWT)来实现。
3. 对于每一个尺度,计算其尺度谱。尺度谱反映了信号在不同尺度上的频率分布情况。可以使用细节系数的平方来作为尺度谱的估计值。
4. 可以将尺度谱进行可视化,通常以二维图像的形式展示。水平轴表示时间或样本点的位置,垂直轴表示尺度。在图像中,颜色表示信号在不同尺度上的能量或强度。
通过分析小波尺度谱,我们可以获得信号在不同尺度上的频率分布信息,并且可以检测到信号中的瞬态、周期性以及突变等特征。这对于信号处理、模式识别、振动分析等领域具有重要的应用价值。
📚2 运行结果





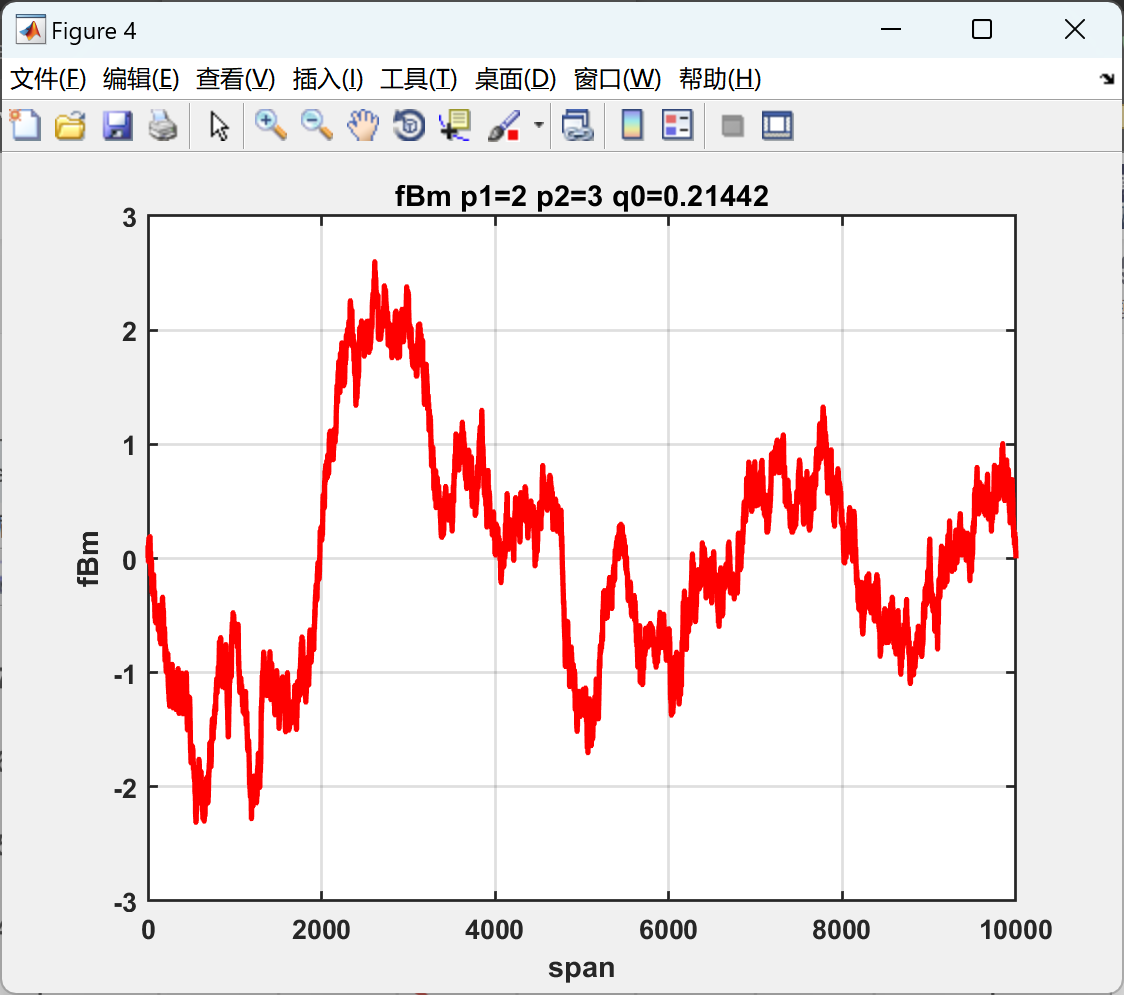
1和3就不一一展示了。
部分代码:
function SDF=TwoComponentSDF(q,cs,p1,p2,q0)
%USAGE SDF=TwoComponentSDF(q,cs,p1,p2,q0)
%
%PUURPOSE evaluate SDF(q)=cs*q^p1 for q<q0
% cs*q0^(p1/p2)*q^p2
%INPUTS:
% q=spatial wavenumber (vector)
% cs=turbulent strength (scalar)
% p1=spectral index for q<=q0 (scalar)
% p2=spectral index for q>q0 (scalar)
n=length(q); n1=find(q<=q0);
n2=max(n1)+1:n;
if n1==1
SDF=cs*q.^(-p2);
else
SDF=cs*q(n1).^(-p1);
SDF=[SDF,cs*q0^(p2-p1)*q(n2).^(-p2)];
end
return
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。
[1]潘龙,潘宏侠,马白雪.基于小波尺度谱重排与排列熵的自动机故障诊断[J].探测与控制学报,2015,37(03):100-104.
[2]杨智,罗国,袁芳芳.自适应小波尺度谱阈值在膈肌信号降噪的应用[J].计算机应用,2013,33(09):2679-2682.
[3]李宏坤,练晓婷,周帅.小波尺度谱同步平均在弱信息识别中的应用[J].机械工程学报,2013,49(05):32-38.