0 概览

动态规划的题型，一定是要求解最值的，比如最短编辑距离，最长递增子序列，最长公共子序列，求最值得问题，核心一定是穷举，先穷举所有可行解，再找出最优的。状态转移方程是最重要的，最关键的，因为重叠子问题与最优子结构可以理解为动态规划的两个特性，状态转移方程是求解动态规划问题的一个思路，所以说是最关键的，特性的意思就是说，发现这个题有重叠子问题和最优子结构，就知道这是一个dp问题，而解法还得是状态转移方程，状态转移方程就是为了穷举，找出最优解。

1 步骤

1. 明确状态（会变的，$dp$函数参数）
2. 明确选择（递归找到最优）
3. 明确$dp$定义（状态方程）
4. 明确$bc$（比如说，第一行，第一列，全初始化某些值）

1.1 框架

// 初始化 bc
dp[0][0][...] = base;

//状态转移
for 状态1 in 状态1的所有取值:
	for 状态2 in 状态2的所有取值:
		for ...
			dp[状态1][状态2][...] = 求最值(选择1,, 选择2, ...)

在经典dp问题当中，最小编辑距离当中，就是分为以上的几步状态，初始化$basecase$，穷举，进行状态转移。

---

• 图片来自东哥
  

---

2 刷题

2.1 斐波那契数列

---

---

2.1.1 题解

如果是采用递归的方法写的话，会发现算法的计算效率有点低，因为递归的时间复杂度为：递归函数调用的次数 * 递归函数本身的复杂度。并且递归还会造成很多的冗余计算，所以为了防止递归造成冗余计算，就想出了一个备忘录递归，这样可以避免进行冗余计算（把树形的结构转换成了链式的结构，备忘录可以防止重复计算），这是一个自顶向下的dp思想。

---

• 图片来自东哥，先自顶向下的去寻找，接着自顶向上的回溯。
  

---

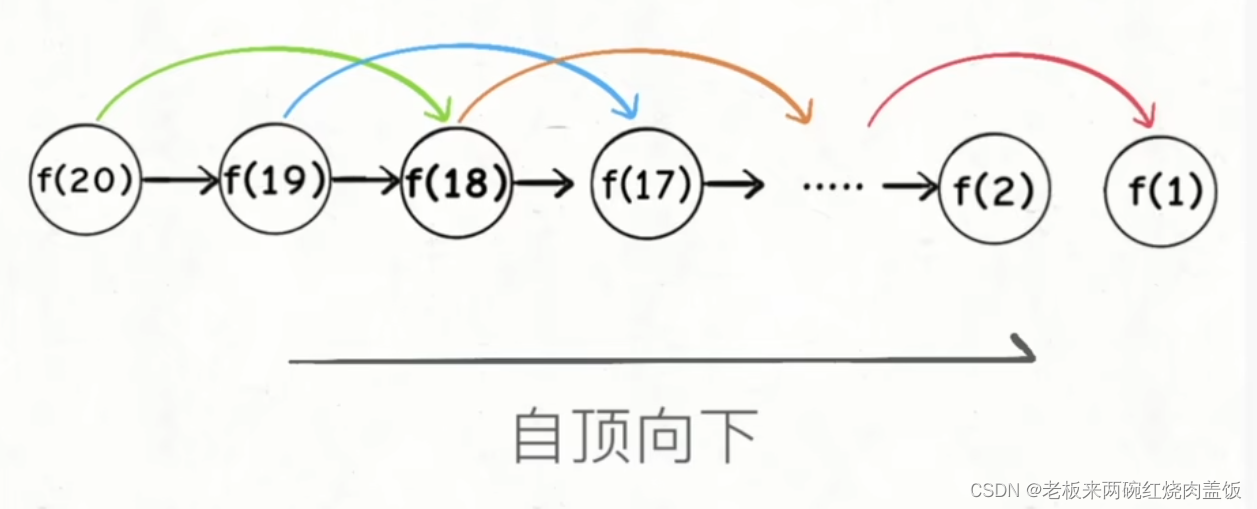
最后，因为只需要前两个数的值，就能推到要推的数，所以继续进行优化，得到最终版本。

2.1.2 Code

//递归
class Solution {
public:
    int fib(int n) {
        if (n == 0 || n == 1) return n;
        return fib(n - 1) + fib(n - 2);
    }
};

//备忘录
class Solution {
private:
    vector<int> memo;
public:
    int fib(int n) {
        memo.resize(n + 1);
        return helper(memo, n);
    }

    int helper(vector<int> memo, int n)
    {
        if (n == 0 || n == 1) return n;
        if (memo[n] != 0) return memo[n];
        memo[n] = helper(memo, n - 1) + helper(memo, n - 2);
        return memo[n];
    }
};

//空间复杂度优化
class Solution {
public:
    int fib(int n) {
        //base case
        if (n == 0 || n == 1) return n;

        //递推
        int prev = 0, curr = 1;
        for (int i = 2; i <= n; ++i)
        {
            int sum = prev + curr;
            prev = curr;
            curr = sum;
        }
        return curr;
    }
};

2.1.3 结果

---

---

2.2 零钱兑换

---

---

2.2.1 题解

因为这是要求计算所需的最少硬币的个数，这是一个求最值的问题，所以想到可以使用dp来进行求解，利用框架几步走，一步一步来就行。

2.2.2 Code

class Solution {
    //状态：目标金额amount（函数参数中会变化的量）
    //选择：coins数组中列出的所有硬币面值（导致你状态变化的就是选择）
    //函数的定义：凑出总金额amount，至少需要coinChange(coins, amount)枚硬币
    //base case：amount == 0时，需要0枚硬币；amount < 0时，不可能凑出，return -1
private:
    vector<int> memo;
public:
    int coinChange(vector<int>& coins, int amount) {
        memo.resize(amount + 1);
        memo.insert(memo.begin(), memo.size(), -666);//先让其元素为负值
        //base case
        return dp(coins, amount);
    }
    int dp(vector<int> coins, int amount){
        if (amount == 0) return 0;
        if (amount < 0) return -1;
        //查备忘录，防止重复计算

        if (memo[amount] != -666) return memo[amount];

        int res = INT_MAX;
        for (int coin : coins)
        {
            //计算子问题的结果
            int subProblem = dp(coins, amount - coin);
            //子问题无解则跳过
            if (subProblem == -1) continue;
            //在子问题当中选择最优解，然后+1
            res = min(res, subProblem + 1);
        }
        memo[amount] = (res == INT_MAX) ? -1 : res;
        return memo[amount];
    }
};

2.2.3 结果