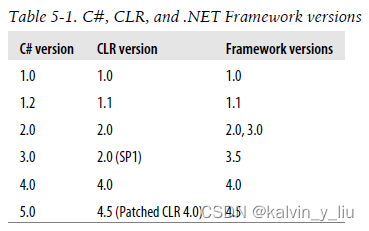
由数据范围反推算法复杂度以及算法内容 - AcWing

常用代码模板3——搜索与图论 - AcWing

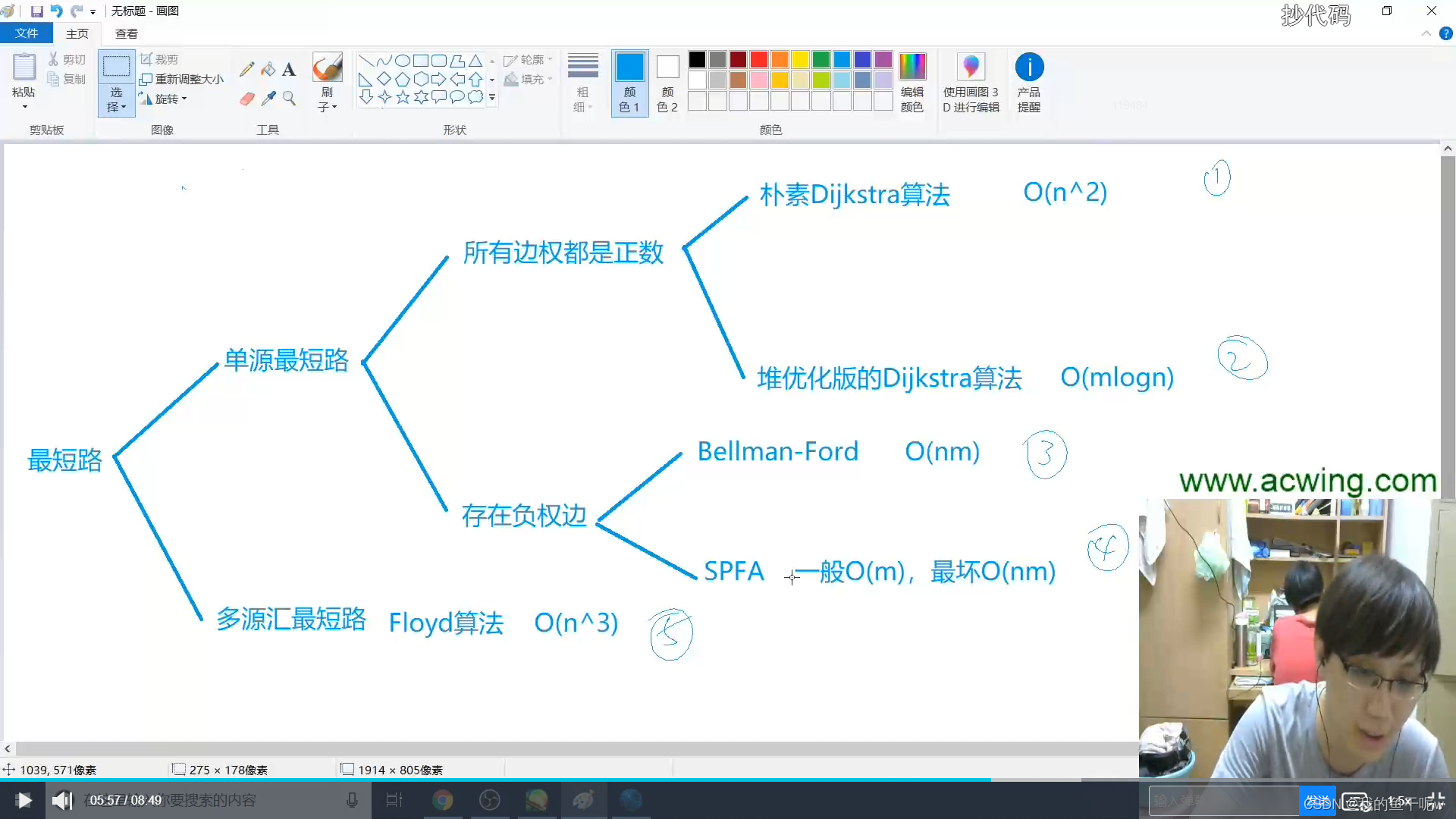
基本思想：

        逐遍的对图中每一个边去迭代计算起始点到其余各点的最短路径，执行n-1遍，最终得到起始点到其余各点的最短路径。（n为连通图结点数）

与dijkstra算法的区别：

        1. 迪杰斯特拉算法是借助贪心思想，每次选取一个未处理的最近的结点，去对与他相连接的边进行松弛操作；贝尔曼福特算法是直接对所有边进行n-1遍松弛操作。

        2. 迪杰斯特拉算法要求边的权值不能是负数；贝尔曼福特算法边的权值可以为负数，并可检测负权回路。

名词解释：

1. 松弛操作：不断更新最短路径和前驱结点的操作。

2. 负权回路：绕一圈绕回来发现到自己的距离从0变成了负数，到各结点的距离无限制的降低，停不下来。

        若有dist[b] > backup[a] + w，则表示途中存在从源点可达的权为负的回路。

        我们循环的次数也是有意义的，例如例题，我们抵代k次，最短距离就是从1号点经过不超过k条边到达n的距离

        bellman-ford算法可以检测负权环。正常情况，最差 n - 1次松弛 就可以求出最短路。但是如果存在负权环，是没有最短路的，我们可以通过反复走这条边，来缩短距离。如果要检测负权环，我们只需要在bellman-ford运行完成后，再进行一轮松弛操作。如果松弛操作成功，那么证明有负权环。

        但是一般找负环是不用Bellman-ford算法，一般是用SPFA算法，这里我们只要知道Bellman-ford算法可以找负权回路即可。

        例题中，在遍历每条边前，我们会先备份上一轮的各点的距离，防止在本次遍历每条边时发生串联，例如样例中的，各点的初始距离为正无穷，我们第一次枚举的1到2，距离变成了1，如果不采用备份，我们遍历2到3时，距离就会变成1+1=2，此时用了两条边，并不符合题目要求，反之，当我们备份数组后，遍历2到3的距离就是正无穷+1和3比较，仍是3；以及因为题目中存在负权边，所以dist[n]的值不一定为0x3f3f3f3f

853. 有边数限制的最短路 - AcWing题库

给定一个 n 个点 m 条边的有向图，图中可能存在重边和自环， 边权可能为负数。

请你求出从 1 号点到 n 号点的最多经过 k 条边的最短距离，如果无法从 1 号点走到 n 号点，输出 impossible。

注意：图中可能 存在负权回路 。

输入格式

第一行包含三个整数 n,m,k。

接下来 m 行，每行包含三个整数 x,y,z 表示存在一条从点 x 到点 y 的有向边，边长为 z。

点的编号为 1∼n。

输出格式

输出一个整数，表示从 1 号点到 n 号点的最多经过 k 条边的最短距离。

如果不存在满足条件的路径，则输出 impossible。

数据范围

1≤n,k≤500
1≤m≤10000
1≤x,y≤n
任意边长的绝对值不超过 10000。

输入样例：

3 3 1
1 2 1
2 3 1
1 3 3

输出样例：

3

#include<iostream>
#include<algorithm>
#include<cstring>

using namespace std;

const int N = 510, M = 10010;
int n, m, k;
int dist[N], backup[N];

struct Edge
{
    int a, b, w;
}edges[M];

void bellman_ford()
{
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;
    
    for(int i = 0; i < k; i++)
    {
        memcpy(backup, dist, sizeof dist);
        //备份一下距离数组 因为有可能会发生串联
        //比如样例 我们更新了1到2的距离此时2的距离为1 
        //然后用2号点来更新距离就会将3号点的距离更新为2
        //但是我们最多只能用1条路径 而此时发生了串联就将3号点的距离变成了2发生错误
        for(int j = 0; j < m; j++)
        {
            int a = edges[j].a, b = edges[j].b, w = edges[j].w;
            dist[b] = min(dist[b], backup[a] + w);
        }
    }
}

int main()
{
    cin >> n >> m >> k;
    for(int i = 0; i < m; i++)
    {
        int a, b, w;
        cin >> a >> b >> w;
        edges[i] = {a, b, w};
    }
    
    bellman_ford();
    
    if(dist[n] > 0x3f3f3f3f / 2) cout << "impossible";
    //因为存在负权边，所以不写成dist[n] == 0x3f3f3f3f
    else cout << dist[n];
    
    return 0;
}