1. 动机

• 一个好的模型需要对输入数据的扰动鲁棒（不管一张图片加入多少噪音，也能看清这张图片）
  • 使用有噪音的数据等价于Tikhonov正则
  • 丢弃法：在层之间加入噪音

输入数据加入随机扰动可以防止过拟合，泛化性更好，等价于一种正则方式。现在对噪音的添加方式从输入位置放到了层间位置。

Q： 之前的视频说，有了噪音才会出现过拟合，为什么这里又说加入随机扰动又可以防止过拟合？
A：我的理解是，之前的噪音是固定的，如果模型学习到了一组参数w和b，可以很好得拟合数据，但是w很大，那么噪音也会因为这个w而被放大，那在预测的时候会很不准确，会出现过拟合。

随机加入扰动，在一次更新参数的时候，也许w和b会学得很大，但下一次噪音又不同了，又会再次学习w和b，因为可以理解为在一定程度上限制参数大小，防止过拟合。

2. 无偏差地加入噪音

假设x是一层到下一层之间的输出，希望对x加入噪音得到x’，但是希望即使加了噪音，不要改变期望，就是希望数据求平均之后还是一样的。

ps：E[x] = x

p的概率变成0，1-p的概率把数据变大，因为p在0～1之间。

3. 使用丢弃法

• 通常将丢弃法作用在隐藏全连接的输出层上。

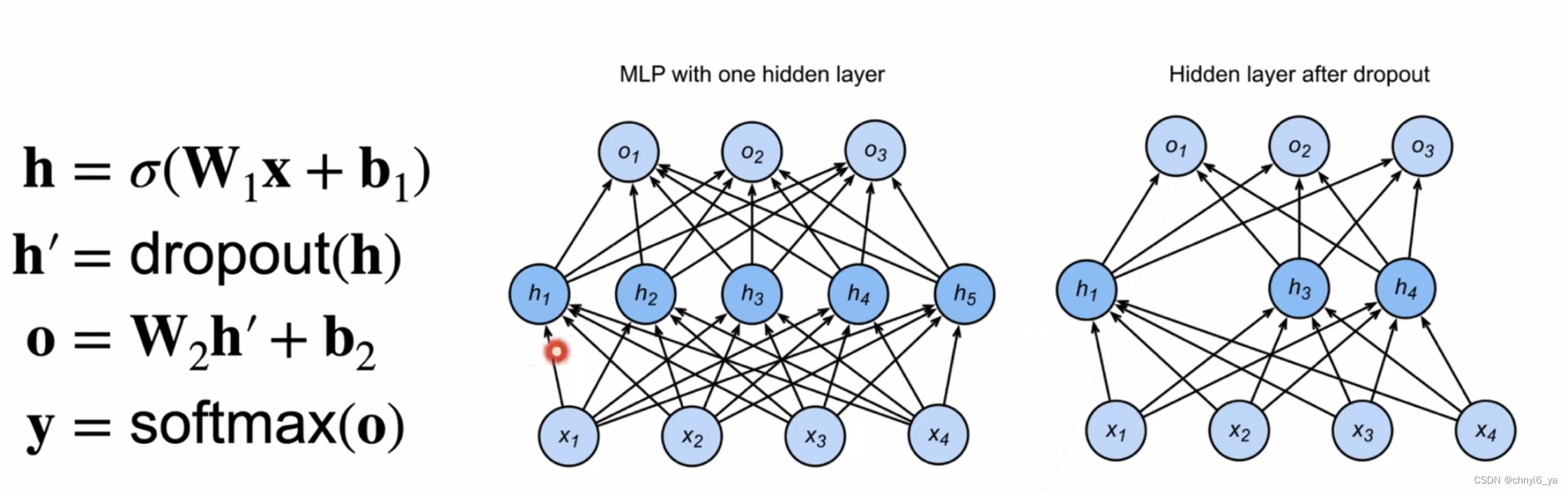
4. 推理中的丢弃法

• 正则项只在训练中使用：他们影响模型参数的更新
• dropout也是正则化，只在训练时使用，训练时学习参数w和b
• 在推理/预测过程中，丢弃法直接返回输入
  • h = dropout（h）
  • 这样也能保证确定性的输出

5. 总结

• 丢弃法将一些输出项随机置0来控制模型复杂度
• 常作用在多层感知机的隐藏层输出上
• 丢弃概率是控制模型复杂度的超参数
• 常见丢弃概率：0.1 ，0.5，0.9