【C/C++】斐波那契数列数列系列问题详解

news2024/9/21 16:43:54

🍎 博客主页：🌙@披星戴月的贾维斯
🍎 欢迎关注：👍点赞🍃收藏🔥留言
🍇系列专栏：🌙 C++初阶
🌙励志卓越可以成为你努力的动力，追求完美却只会让你身心俱疲。🌙
🍉一起加油，去追寻、去成为更好的自己！

斐波那契数列数列是我们学习递归的入门问题，是一种非常经典的题型，也衍生出了一些更复杂的题型，这一节就让我们彻底理解斐波那契数列系列问题。

在这里插入图片描述

文章目录

🍎、概念介绍
🍎、斐波那契数列系列问题详解
🍎、总结和思考

提示：以下是本篇文章正文内容，下面案例可供参考

🍎、概念介绍

🍉、什么是斐波那契数列？

斐波那契数列（Fibonacci sequence），又称黄金分割数列，因数学家莱昂纳多·斐波那契（Leonardo Fibonacci）以兔子繁殖为例子而引入，故又称为“兔子数列”，指的是这样一个数列：1、1、2、3、5、8、13、21、34、……在数学上，斐波那契数列以如下被以递推的方法定义：F(0)=0，F(1)=1, F(n)=F(n - 1)+F(n - 2)（n ≥ 2，n ∈ N

🍉、怎么定义斐波那契数列

斐波那契数列指的是这样一个数列：1，1，2，3，5，8，13，21，34，55，89…
递推公式
斐波那契数列：1，1，2，3，5，8，13，21，34，55，89…
斐波纳契数列以如下被以递归的方法定义：
f[0] = 0, f[1] = 1；f[n] = f[n -1] + f[n - 2](n >= 2)
这个数列从第三项开始，每一项都等于前两项之和。
显然这是一个线性递推数列。

🍎、斐波那契数列系列问题详解

🍇最入门的斐波那契数列问题
在这里插入图片描述
分析题意：是最基本的斐波那契数列问题，问的就是第n个斐波那契数列的值是多少并且输出出来。
根据我们的递推方程 : f[0] = 0, f[1] = 1；f[n] = f[n -1] + f[n - 2](n >= 2)即可求出

🔥递归示意图：🔥
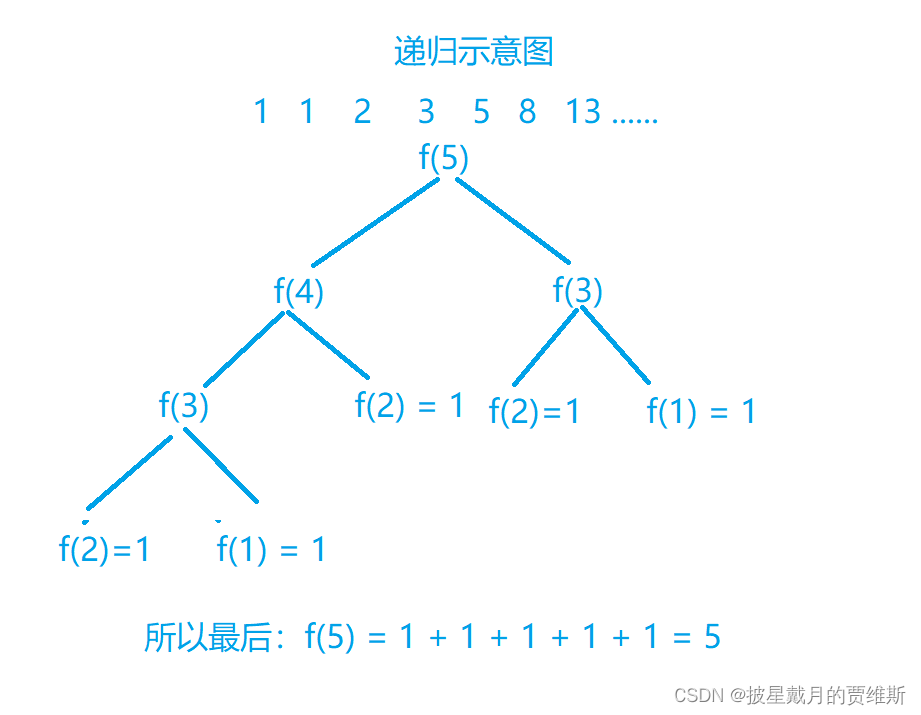
在这里插入图片描述
🔥最原始的递归代码示例：

#include<iostream>
using namespace std;
const int N = 100010;
int fbnq(int n)
{
    if (n == 1 || n == 2) return 1;
    if(n > 2)
    return (fbnq(n - 1) + fbnq(n - 2));
}

int main ()
{
    int n;
    cin >> n;
    cout << fbnq(n) << endl;
}

🔥写法二，利用数组a,实现一个斐波那契数列数组，下标和要输出的数对应一下。

#include<iostream>
using namespace std;
const int N = 100010;
int a[N] = {0}; //全局数组初始化，也可以不用，因为全局数组默认值都是1
void fbnx()
{
    a[1] = 1, a[2] = 1;
    for (int i = 3; i < 100001; i++)
    {
        a[i] = (a[i - 1] + a[i-2]) % 1000000;
    }
}
int main ()
{
    fbnx();
    int n;
    cin >> n;
    cout << a[n] << endl;
}

🍇牛客网：斐波那契凤尾
难度：中等
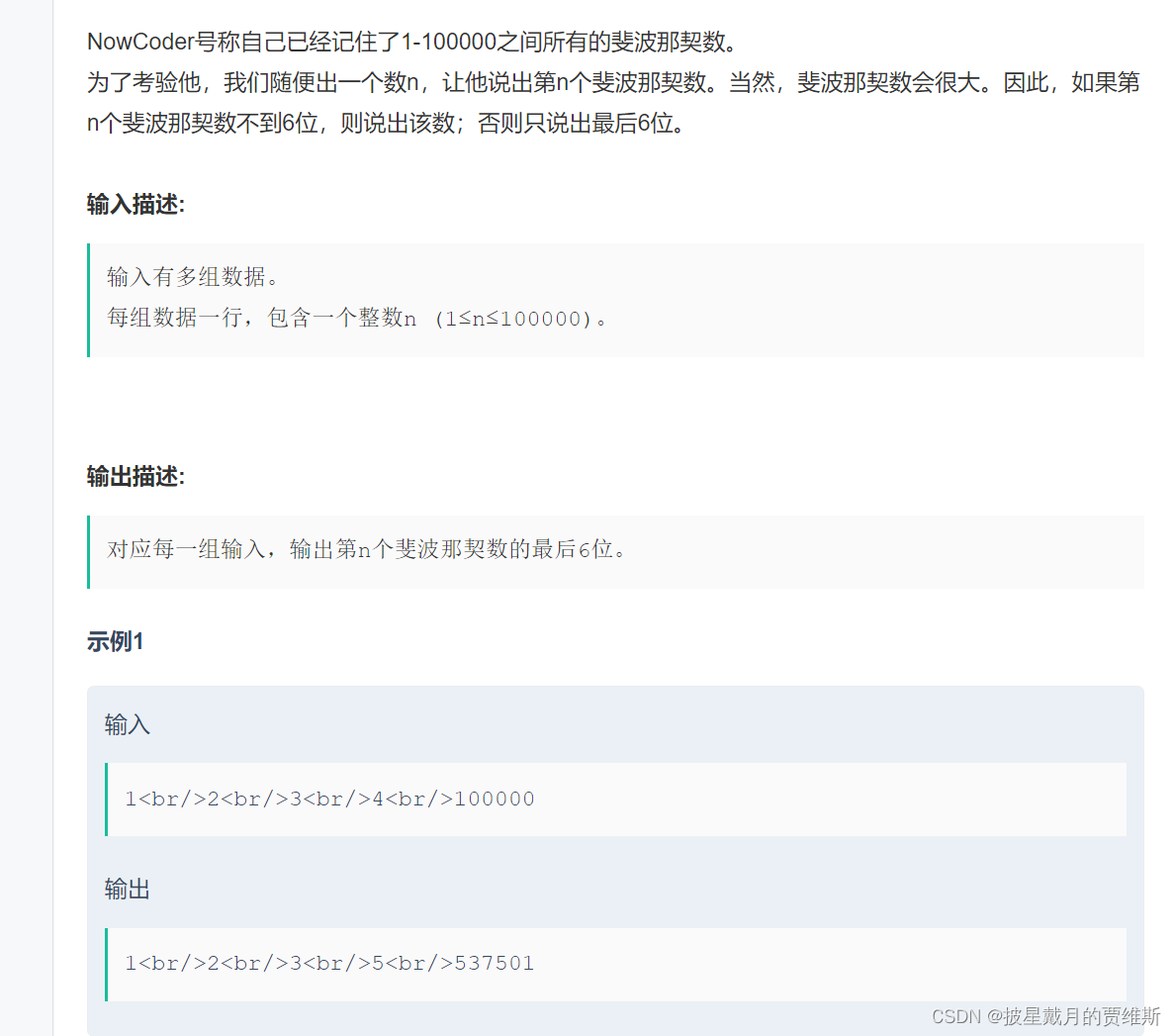
在这里插入图片描述
分析题意：也是让我们输出n对应的斐波那契数，但是是有多组输入，而且是1 - 100000的斐波那契数，肯定超int了，所以只保留最后六位，还是向之前的递归过程。
🔥解法：我们用之前的写法2，建立一个斐波那契数列数组

🔥代码示例：

#include<iostream>
#include<string>
#include<vector>
#include<algorithm>
using namespace std;
const int N = 100010;
int a[N] = {0};
void fbnx()
{
	a[0] = 1, a[1] = 1;
	for (int i = 2; i < 100001; i++)
	{
		a[i] = (a[i - 1] + a[i-2]) % 1000000;//怕超Int，直接%100万
	}
}
int main()
{
	int n;
	fbnx();
	while (cin >> n)
	{
		if (n < 29)
		{
			printf("%d\n", a[n]);
		}
		else
		{
			printf("%06d\n", a[n]);
		}
		
	}

	return 0;
}

🍇牛客网：星际密码
难度：较难
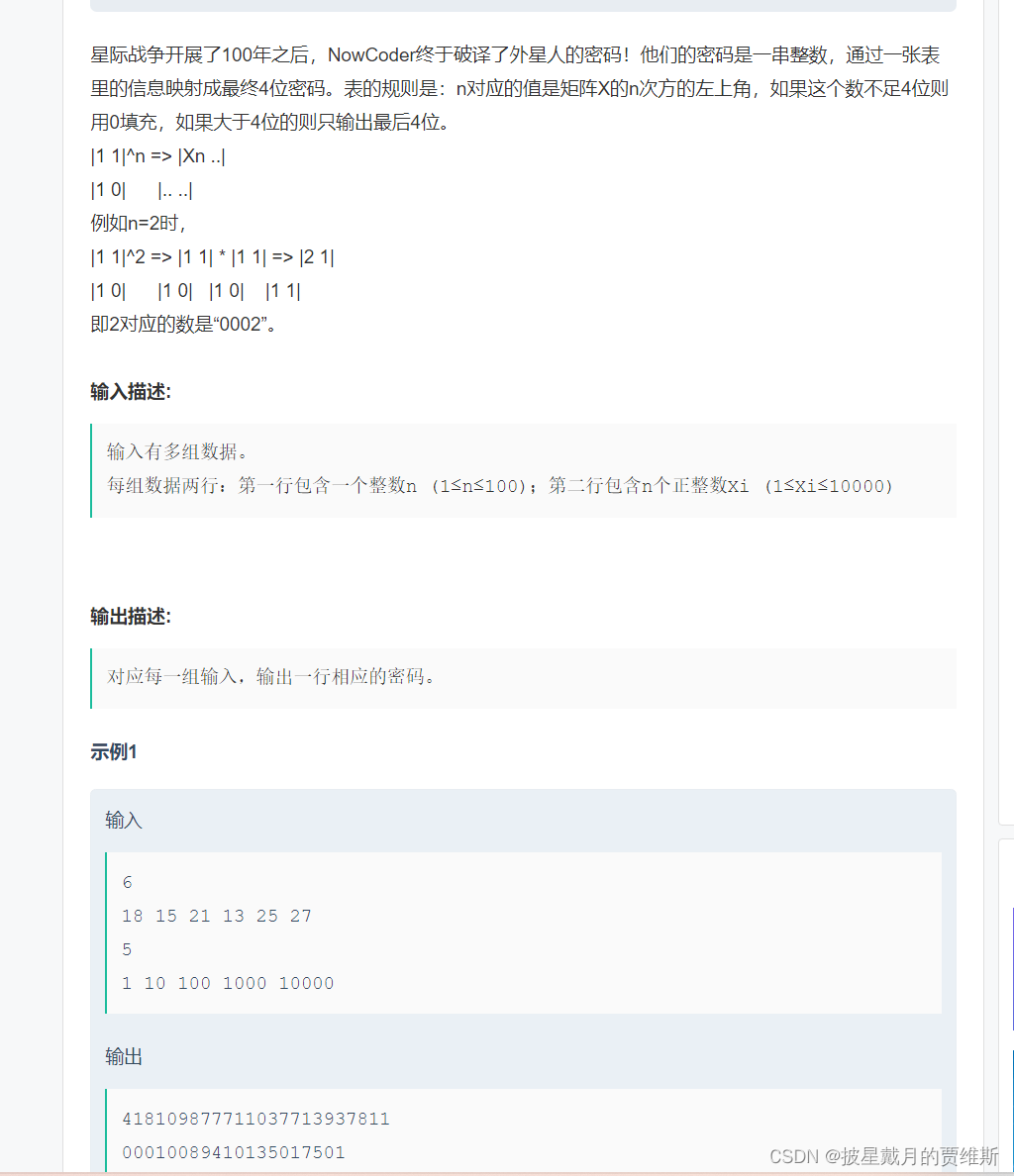
在这里插入图片描述
分析题意：我为什么觉得这道题较难，就是因为本题题意比较难理解。矩阵运算和斐波那契数列结合了起来

🔥所以这道题的解法就是初始化斐波那契数列，每次获取对应数据，打印后4位即可。
🔥代码示例：

#include<iostream>
#include<vector>
using namespace std;
int main ()
{
    vector<int> v = {1, 1};//初始化vector
    for(int i = 2;i < 10001; i++)
    {
        v.push_back((v[i - 1] + v[i -2]) % 10000);//取最后四位
    }
    
    int n;
    while(cin >>n)
    {
        int x = 0;
        for(int i = 0; i < n; i++)
        {
            cin >> x;
            printf("%04d", v[x]);
        }
        printf("\n");
    }
    return 0;
}

本题小结：有时候不是因为这道题涉及的算法难，而是你看不懂这道题涉及的算法是啥，而且许多边界我们也是需要控制的，所以这就需要我们多刷题，才能更快，更准地读懂题意。