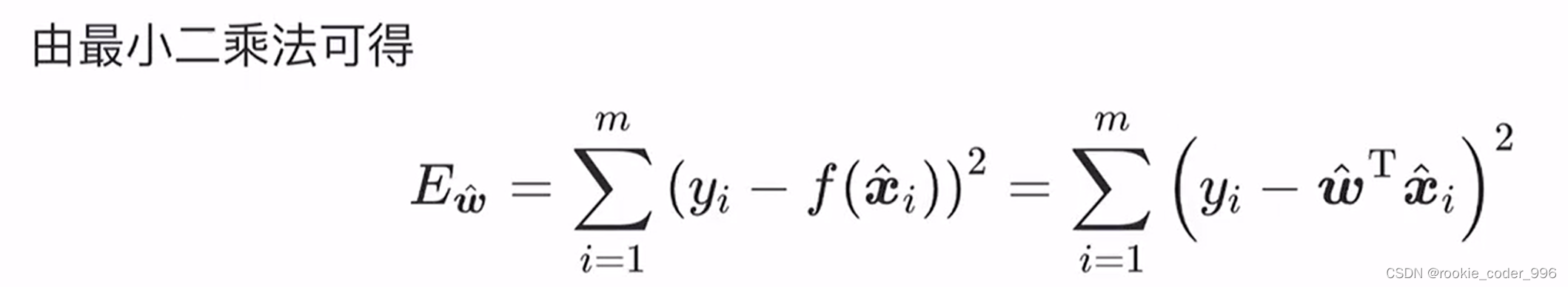🍉 吃瓜系列 教材:《机器学习》 周志华著
🕒时间:2023/7/25
📓 参考:周志华《机器学习》西瓜书啃书指导
📓 参考:第3章-一元线性回归

前言
什么是回归?
回归:确定多个变量间相互依赖的定量关系
回归:预测的输出为连续值
分类:预测的输出为离散的
一、基本形式、思想
试图通过线性的模型,去进行预测
形如:

📓 通俗的理解:机器学习是为了得到一个模型f(x)
那么线性的模型f(x)就可以简化为,得到参数 w 以及 参数 b
当 w b 被确定的时候,我们说得到了一个线性模型
使用线性模型去拟合数据
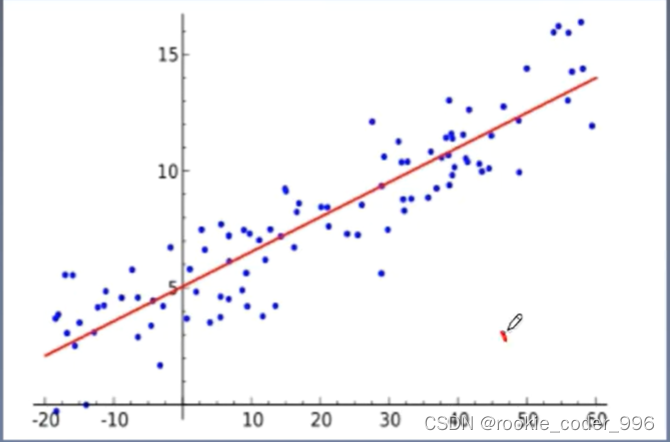
二、线性回归
2.1 一元线性回归
2.1.1 形式
形如 f(x) = wx + b 的形式
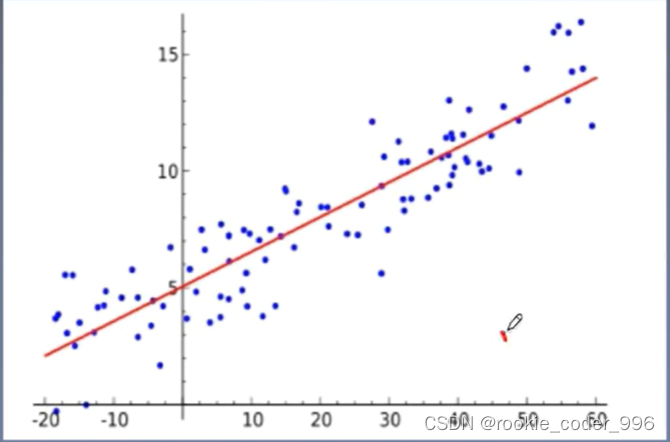
2.1.1 最小二乘法
Q:那么,如何确定 f(x) = wx + b 的最佳 w 和 b 呢?
A:最小二乘法!
当预测值和实际值距离的平方和最小时,就确定了模型中的两个参数( w 和 b)
一旦计算出了α和β的值,就可以使用该模型来预测新的因变量值,只需提供对应的自变量值即可。
缺点:仅考虑了因变量 y 存在误差的情况。但是实际上,原始点的横纵坐标都会有误差存在。
对于回归问题来说,最好的模型就是和实际数据最接近的模型,而最接近的判断在此使用的是最小二乘法

arg min 是argument minimal 的缩写, 用于获得使函数取最小值的参数
PS:在上图中,有一个误区
欧几里得距离的几何意义,不是点到线的距离(正交回归) ❌
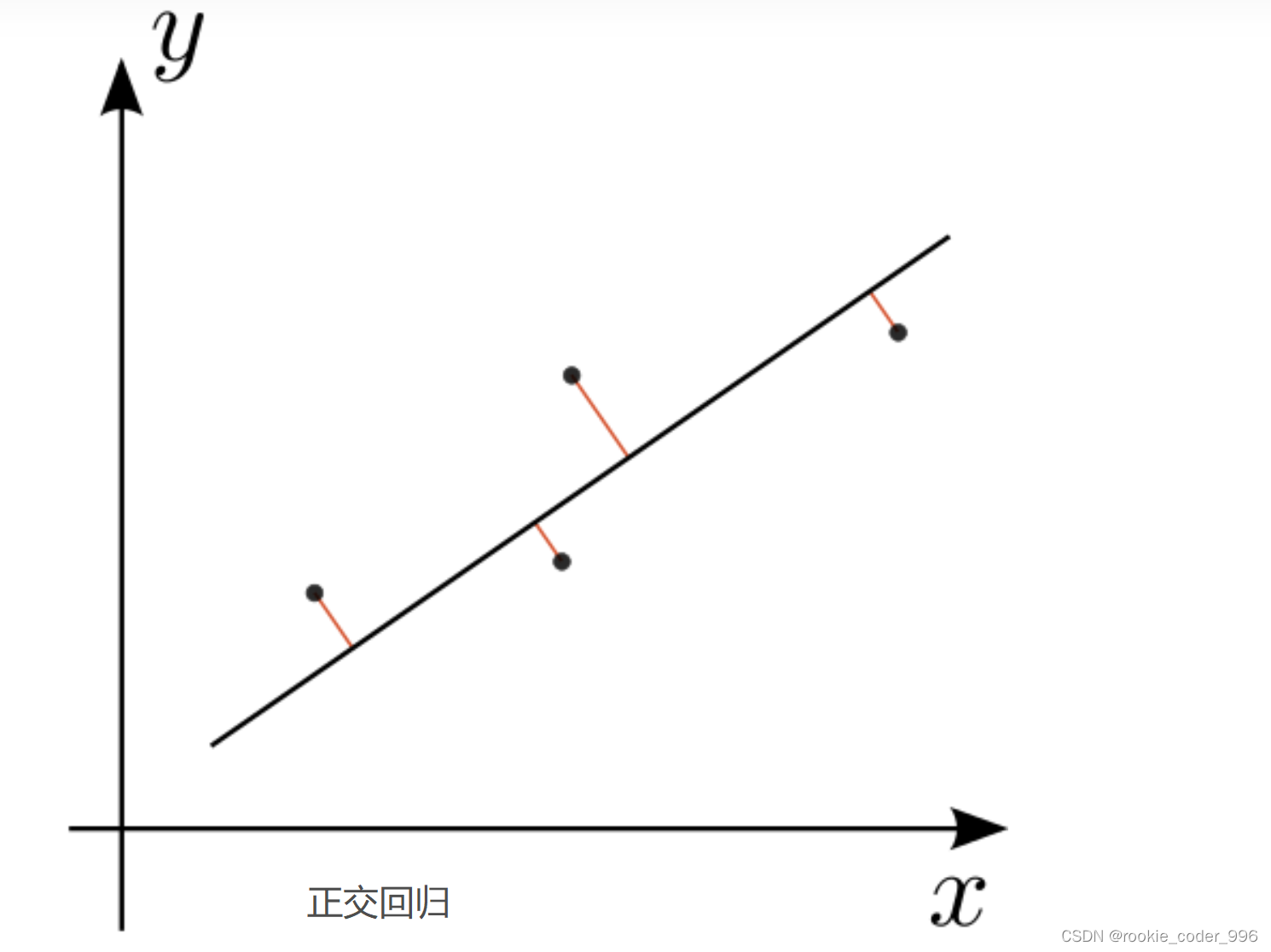
根据欧几里得距离的定义,几何意义应该是这样的:
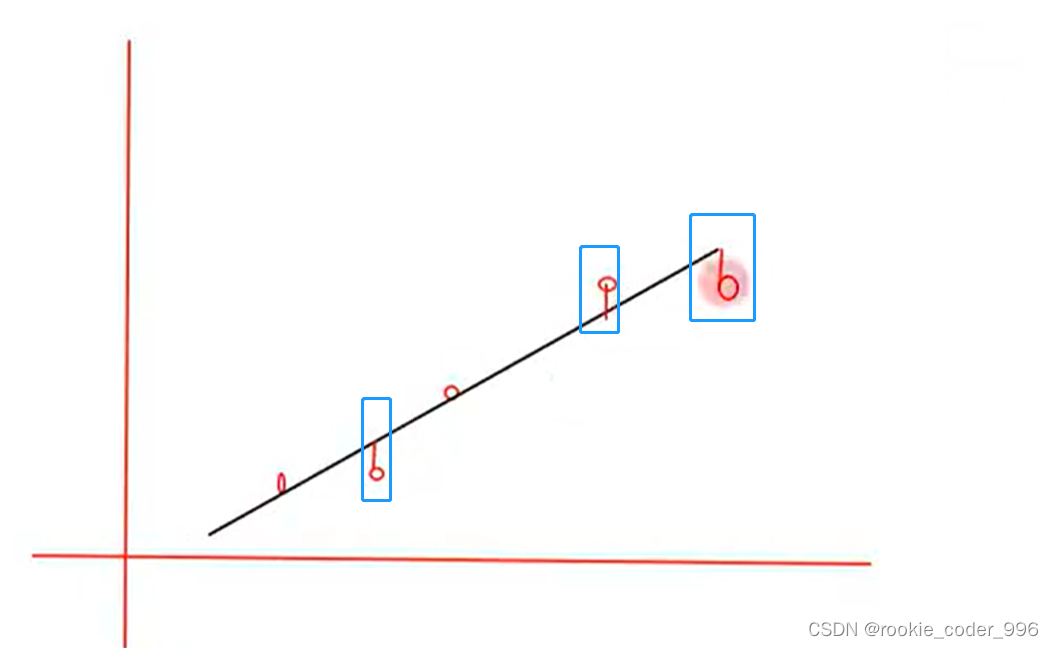
2.1.3 损失函数
上面所使用的均方误差其实一我们用来衡量误差的一个损失函数
常见的损失函数有那些呢?


2.1.4 最小二乘参数估计
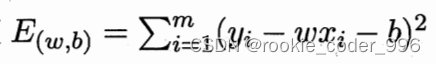
上面讲到,我们需要确定 w 和 b 的合适值,找到最佳的函数
那么,如何确定呢? 求导!!
我们观察到 上面的公式是一个 U 型曲线 差不多 y = x²的那个样子
用国内教材的定义就是 凹函数
我们对凹函数求导,导数 = 0 的点,就是取得最小值的点
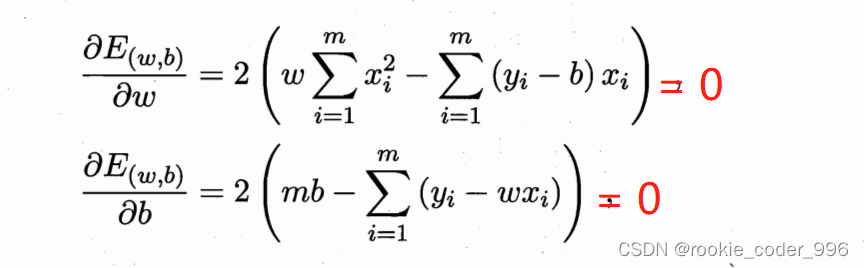
求得最合适的 w 、 b,此时 损失函数(均方误差)最小、拟合效果最好
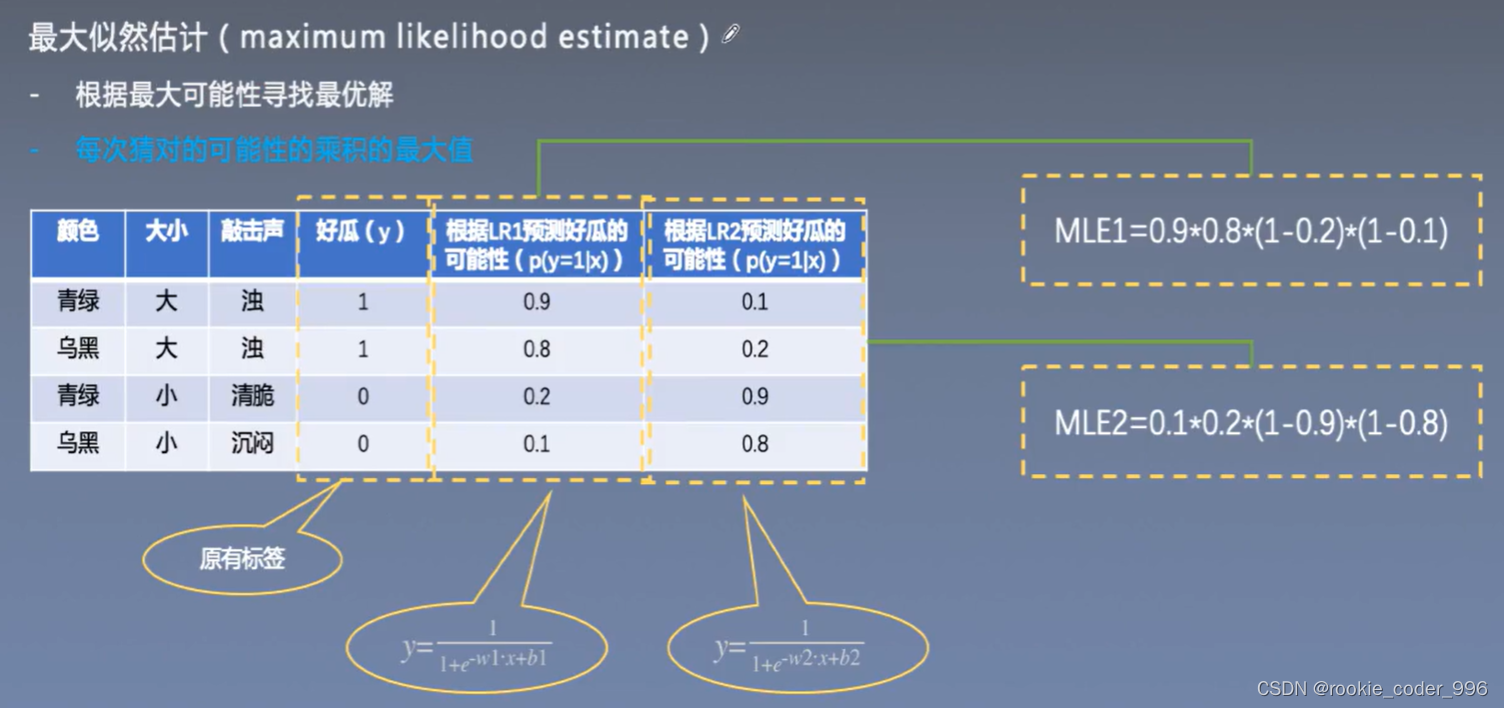
2.1.5 最大似然估计导出最小二乘法

使得观测样本出现概率最大的分布就是代求分布

对数似然函数
key:对数似然函数和似然函数有相同的最大值点~

线性回归我们假设模型是





等价的依据:中间那个减号 后面的最小 结果自然最大
最大似然估计:使得观测样本出现概率最大的分布就是代求分布
最小二乘估计:均方误差最小
2.1.6 梯度和海塞矩阵
梯度:多元函数的一阶导数

梯度为什么是列向量?
梯度是一个向量算子,它表示函数在某一点的变化率,因此梯度的结果是一个向量。
在多元函数的情况下,梯度是一个向量值函数。
在直角坐标系中,梯度的每个分量对应于函数在每个坐标轴方向的变化率,因此自然地形成一个列向量,其中每个元素表示函数在某个方向上的变化率。
海塞矩阵:多元函数的二阶导数


此处的凸函数是国外的定义 指的是国内的凹函数
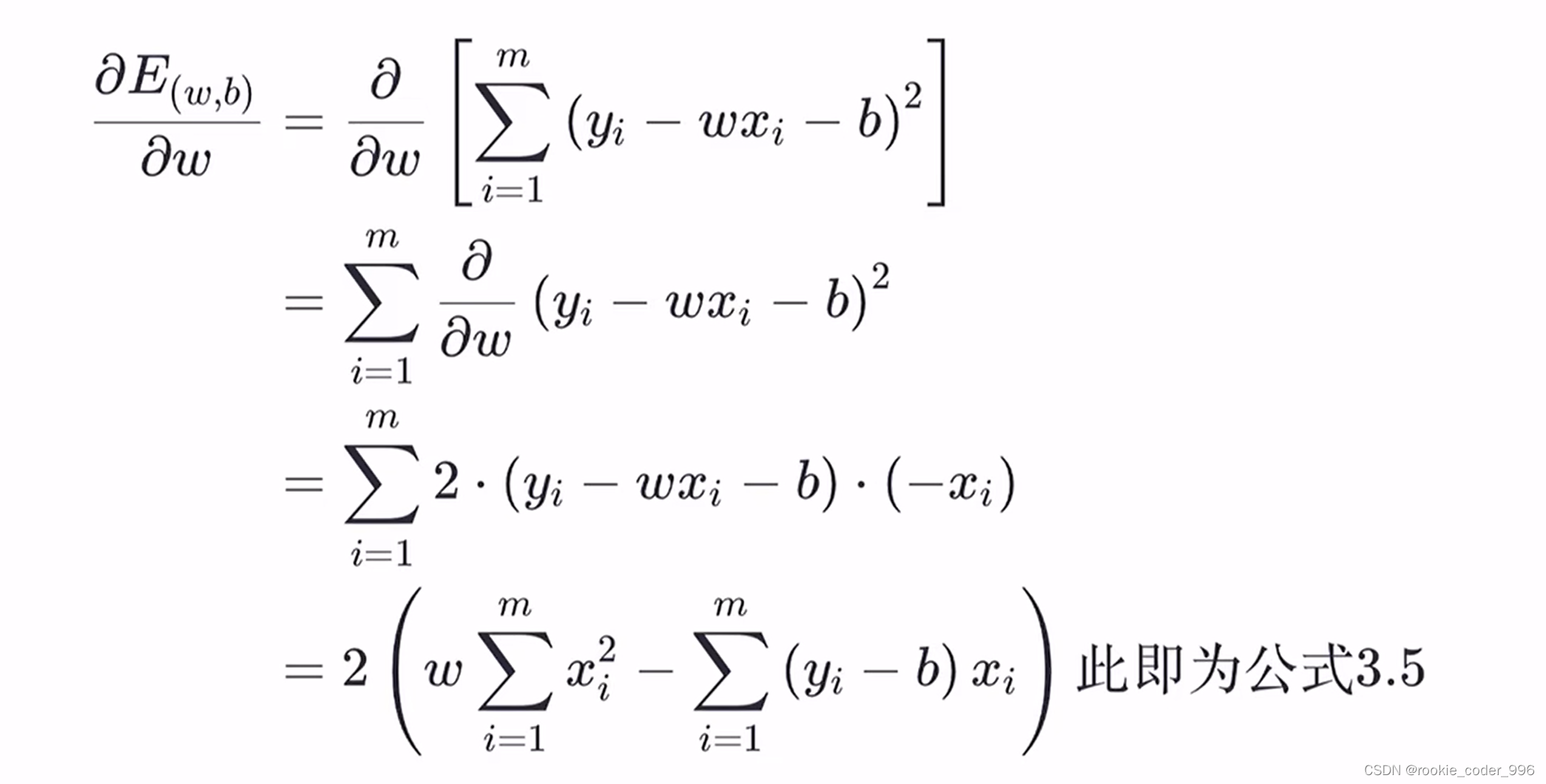

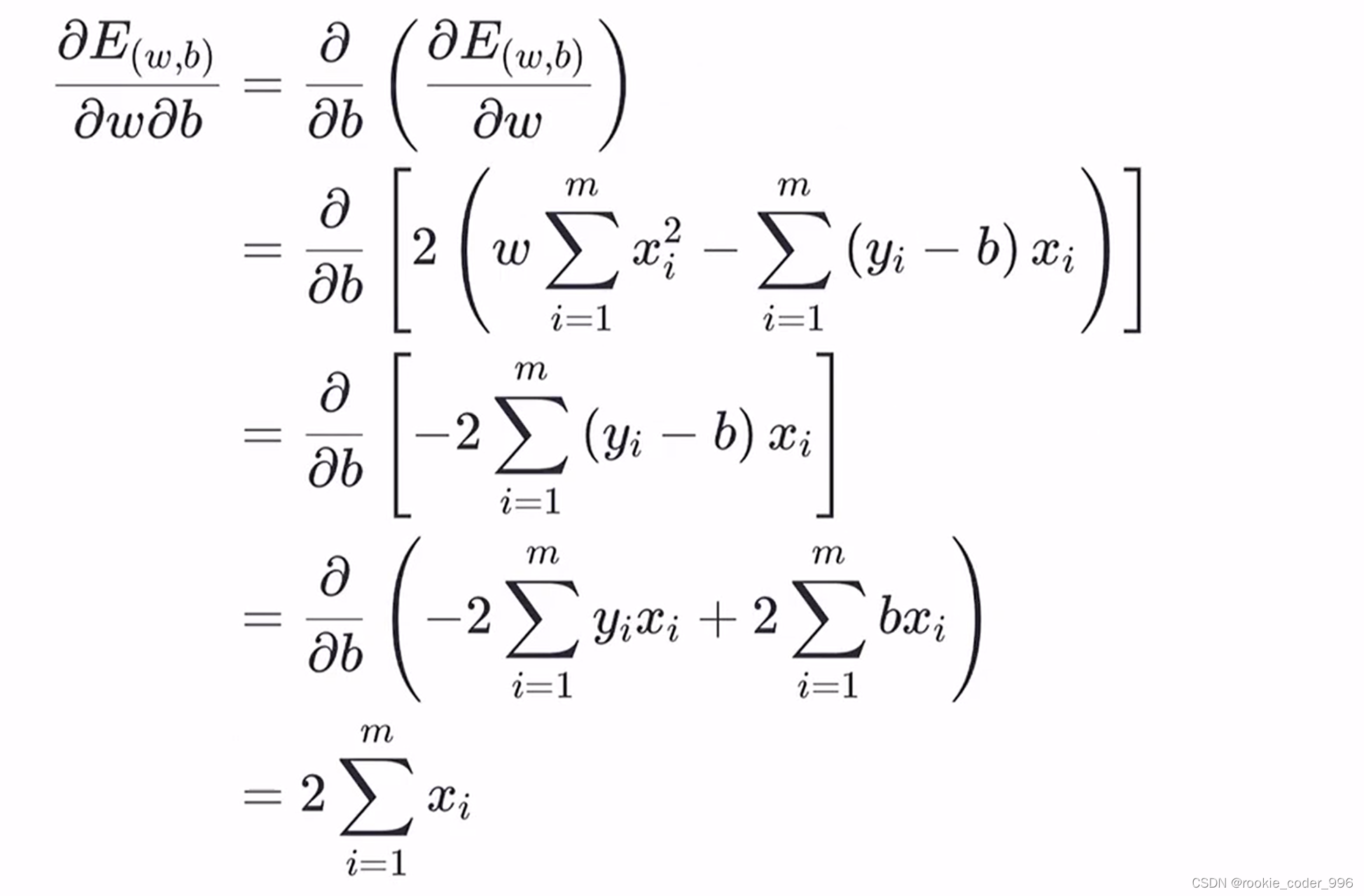
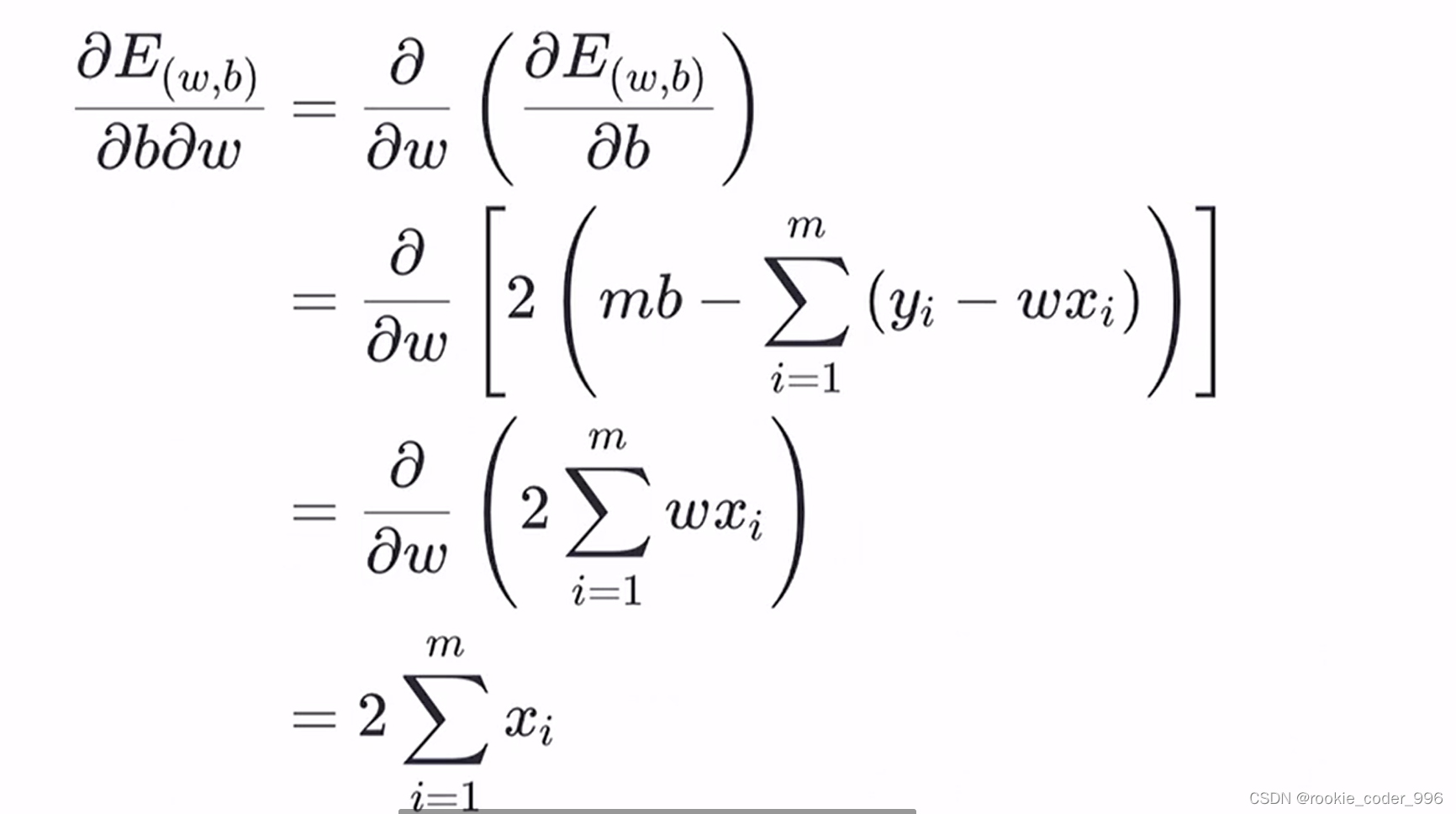






然后带入 b
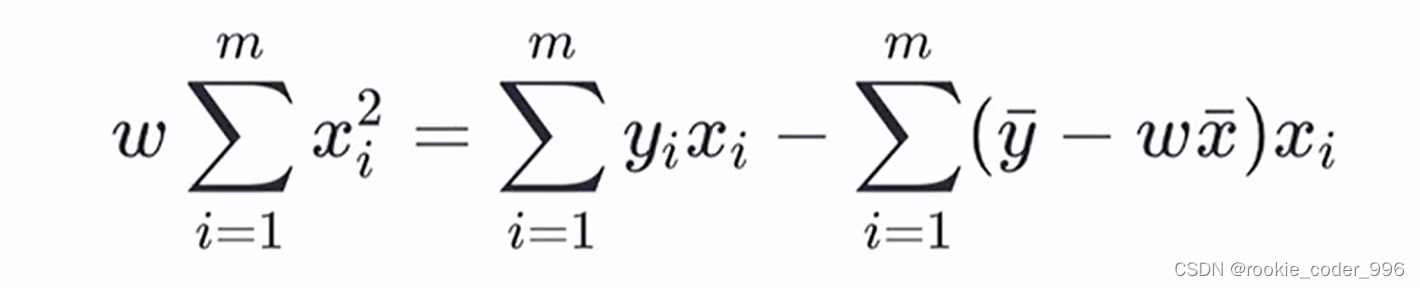
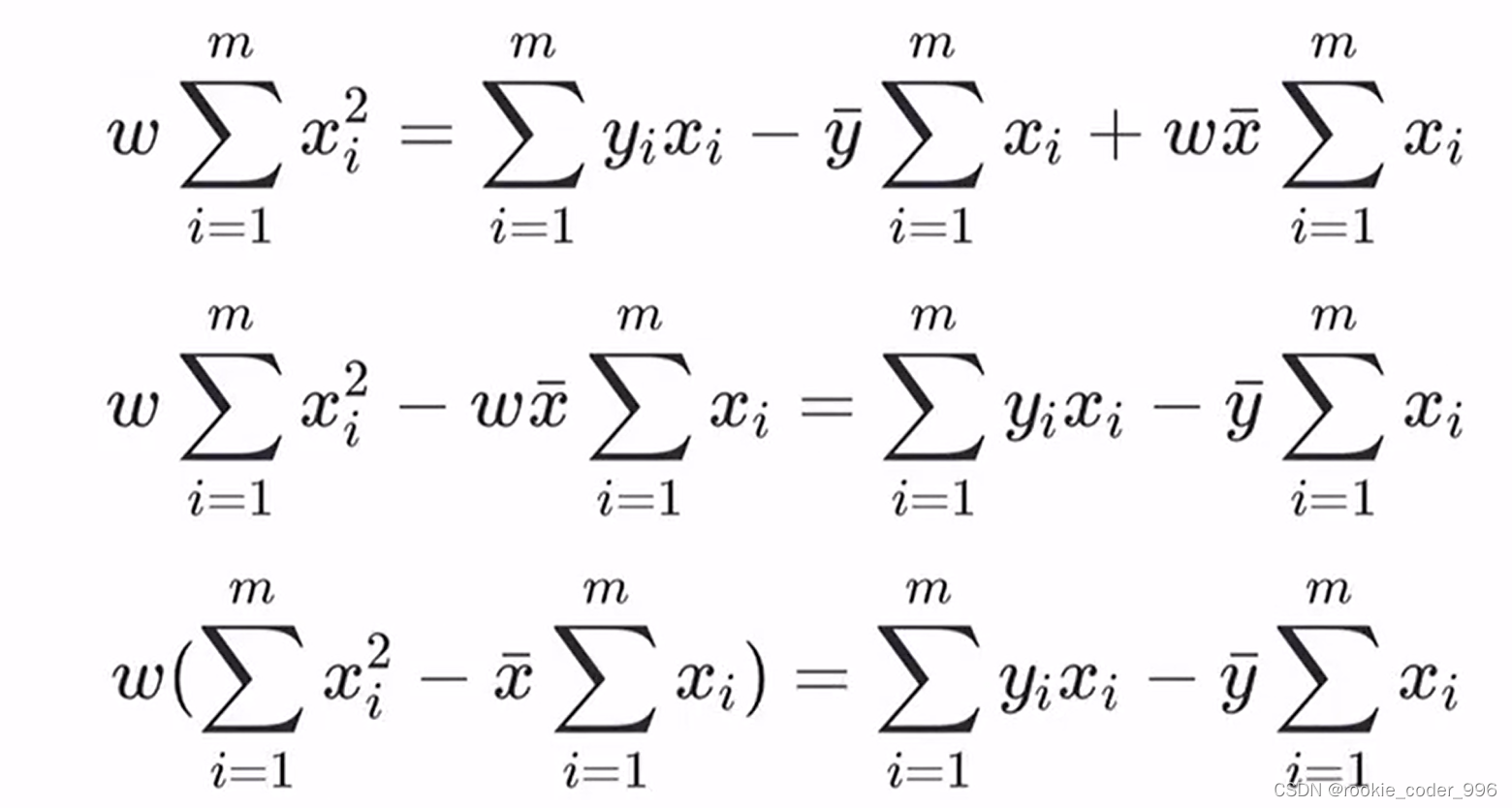
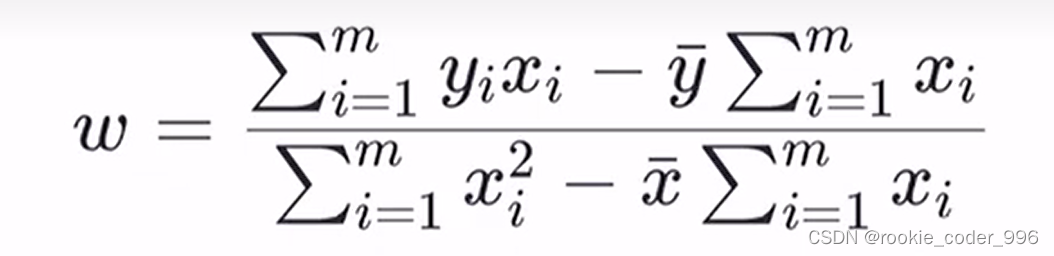
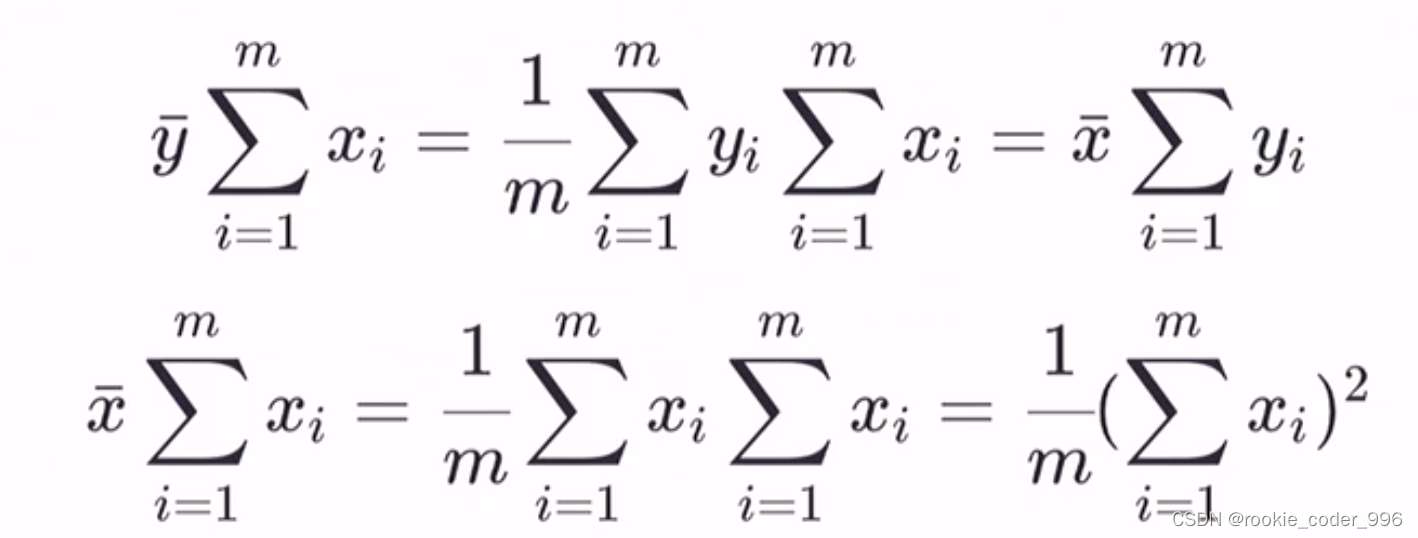
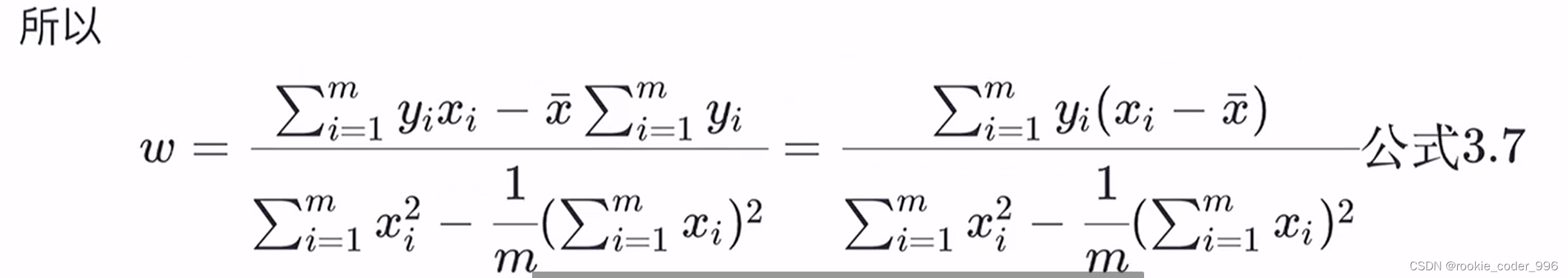
2.2 多元线性回归
在多元线性回归中,我们试图找到一条最佳拟合曲线,使得自变量和因变量之间的误差最小化。
后面的参数 b 我们理解成 b = b ✖ 1
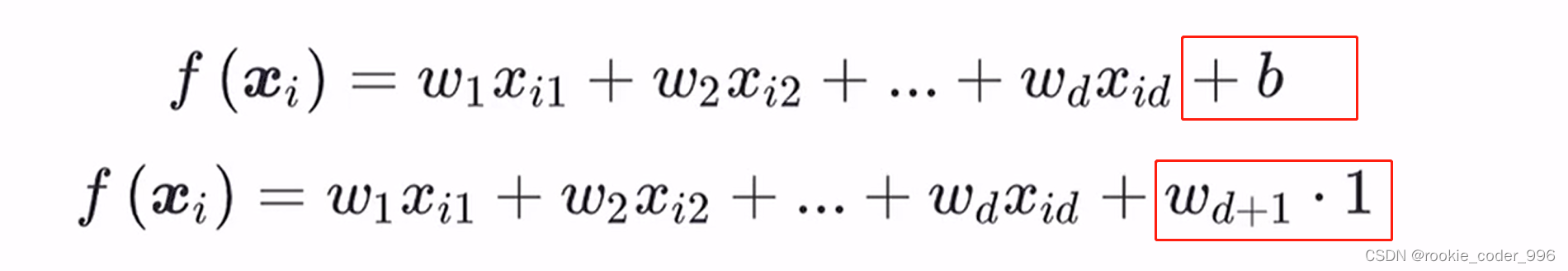

于是 我们构造处理一个权重向量 w 和 一个特征向量 x
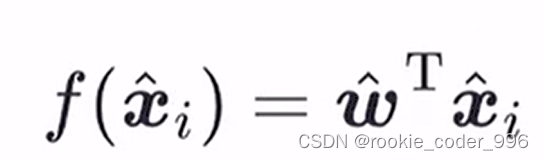
随后 向量化
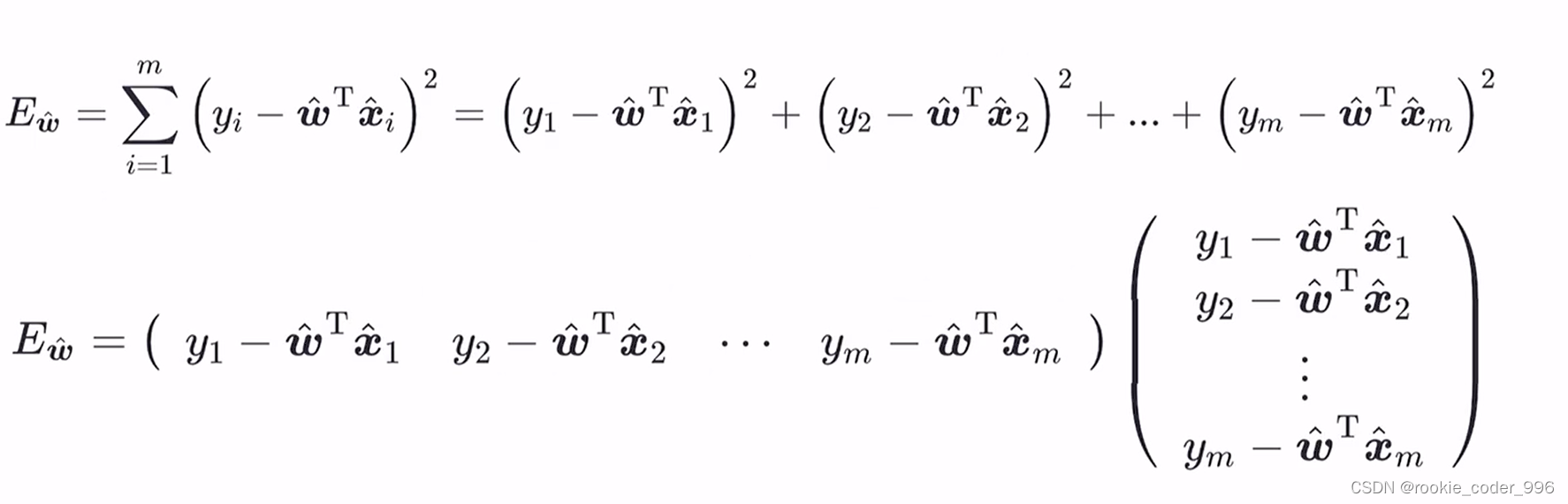

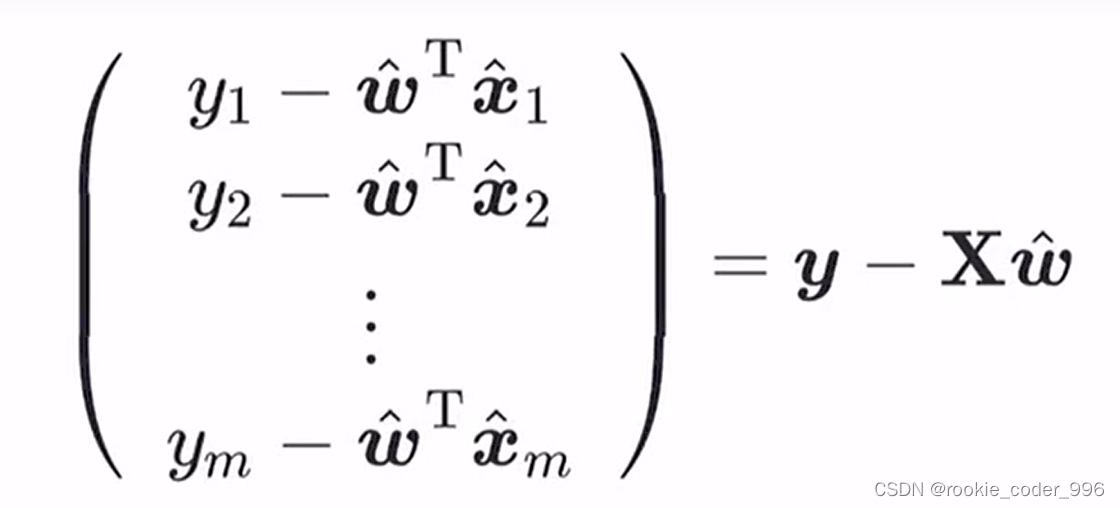
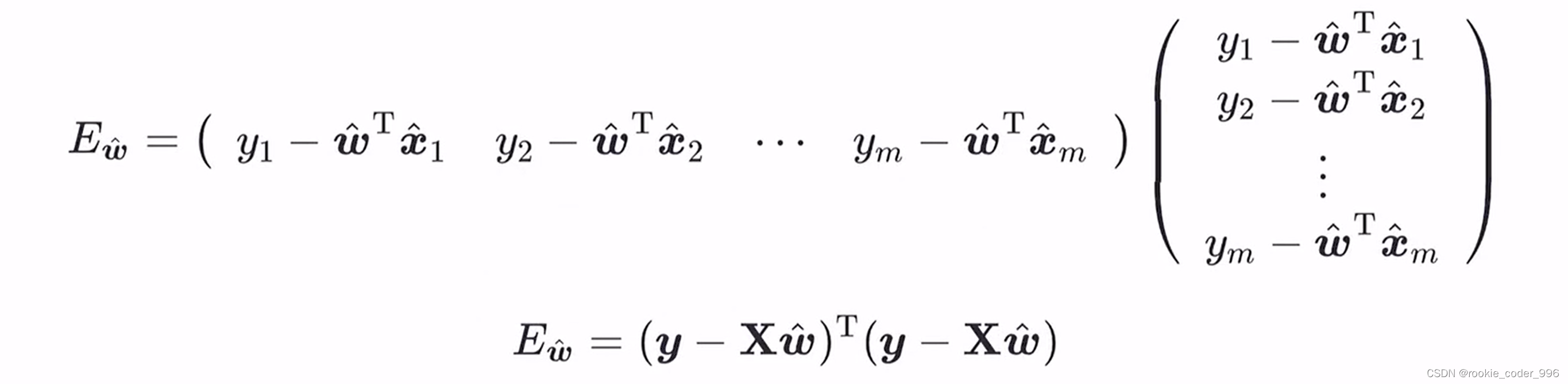



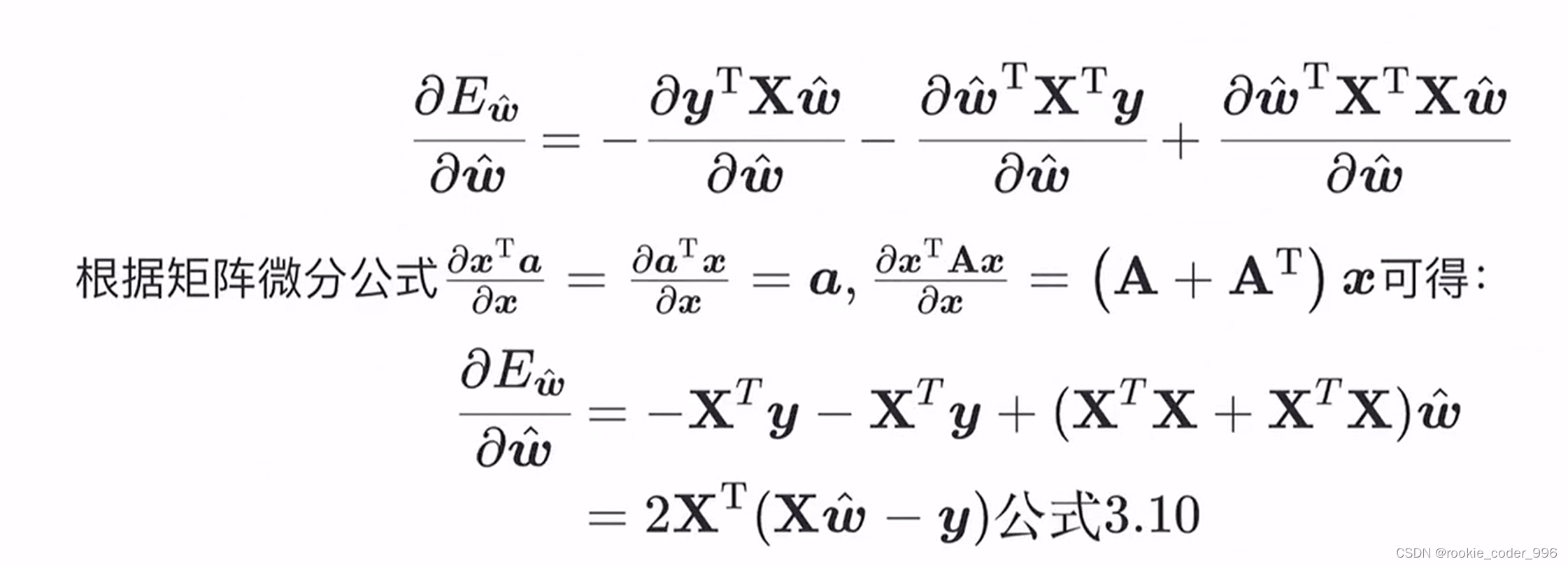


三、线性分类
3.1 对数几率回归

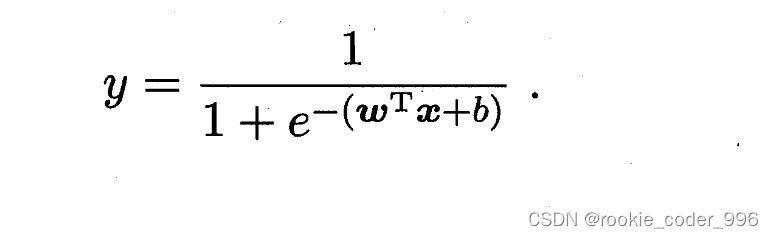

最大似然估计