题目如下：

一个二叉树，树中每个节点的权值互不相同。

现在给出它的后序遍历和中序遍历，请你输出它的层序遍历。

输入格式

第一行包含整数 N，表示二叉树的节点数。

第二行包含 N 个整数，表示二叉树的后序遍历。

第三行包含 N 个整数，表示二叉树的中序遍历。

输出格式

输出一行 N 个整数，表示二叉树的层序遍历。

数据范围

1≤N≤30,
官方并未给出各节点权值的取值范围，为方便起见，在本网站范围取为 1∼N。

输入样例：

7
2 3 1 5 7 6 4
1 2 3 4 5 6 7

输出样例：

4 1 6 3 5 7 2

 中序遍历：遵循规则左根右（1，2，3，4，5，6，7）

后序遍历：遵循规则左右根（2，3，1，5，7，6，4）

如题，它的树长这样：

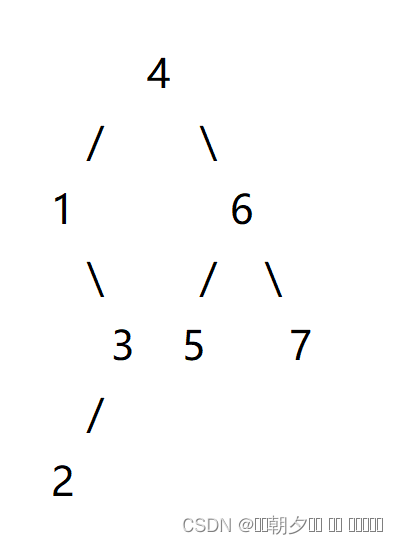
可以得知，后序遍历最后一个位置即为该树的根结点，找到中序遍历中根结点位置，即可判断出左子树与右子树结点个数，即 4 为根结点值，在中序遍历中其前面与后面各有 3 个节点，因此     1，2，3为左子树各结点值，5，6，7为右结点各结点值，再递归到左子树与右子树重复该操作，即可得到该树的结构

代码如下：

        

#include <iostream>
#include <vector>
#include <queue>
using namespace std;

const int N = 35;

//定义树结构
typedef struct TreeNode{
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode(int value) : val(value), left(nullptr), right(nullptr) {} //构造函数
}TreeNode;

//建立树结构
TreeNode* BuildTree(vector<int>& postorder, vector<int>& inorder, int postEnd, int inStart, int inEnd) {
    if(postEnd <= 0 || inStart >= inEnd)
        return nullptr;
    
    //找到根节点，并开辟空间
    int rootval = postorder[postEnd];
    TreeNode* root = new TreeNode(rootval);
    
    //找到该根节点在中序遍历中的位置
    int rootIndexInInOrder = 0;
    for(rootIndexInInOrder = inStart; rootIndexInInOrder <= inEnd; rootIndexInInOrder++){
        if(inorder[rootIndexInInOrder] == rootval){
            break;
        }
    }
    
    //计算出右子树个数
    int rightTreeSize = inEnd - rootIndexInInOrder;
    
    //递归左右子树
    root->right = BuildTree(postorder, inorder, postEnd - 1, rootIndexInInOrder + 1, inEnd);

    root->left = BuildTree(postorder, inorder, postEnd - 1 - rightTreeSize, inStart, rootIndexInInOrder - 1);
    
    return  root;
}


//树的层序遍历
vector<int> GetLevelOrderVal(TreeNode* root){
    vector<int> res;
    
    if(!root)    return res;
    
    queue<TreeNode*> q;
    q.push(root);
    
    while(!q.empty()){
        auto node = q.front();
        q.pop();
        res.push_back(node->val);
        
        if(node->left)      q.push(node->left);
        if(node->right)     q.push(node->right);
    }
    
    return res;
}

int main(){
    vector<int> postorder(N);
    vector<int> inorder(N);
    
    int n = 0;
    cin >> n;
    
    for(int i = 0; i < n; i++)      cin >> postorder[i];
    for(int i = 0; i < n; i++)      cin >> inorder[i];
    
    TreeNode* root = BuildTree(postorder, inorder, n - 1, 0, n - 1);
    
    vector<int> res = GetLevelOrderVal(root);
    
    for(auto& val : res)
        cout << val << " ";
    cout << endl;
        
    return 0;
}