Carla教程一、动力学模型到LQR

从运动学模型和动力学模型到LQR

模型就是可以描述车辆运动规律的模型。车辆建模都是基于自行车模型的设定，也就是将四个轮子抽象为自行车一样的两个轮子来建模。

1、运动学模型

运动学模型是基于几何关系分析出来的，一般适用于低俗情况下，这种情况可以不考虑轮胎的侧偏特性。另外，这里假设前轮的方向就是当前车辆速度的方向。但是高速情况并非如此。整个控制量可以简化为加速度a和偏航角$\delta$。其中油门代表a为正，刹车代表a为负。偏航角是方向盘的控制量。然后可以定义下面的几个状态量，用来描述车辆当前状态：

• x：车辆当前横轴坐标
• y：车辆纵轴坐标
• v: 车辆速度
• $\phi$：车辆横摆角
  

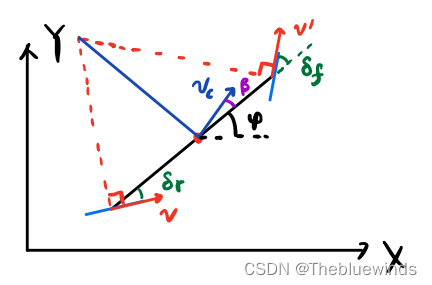
最后推导得到的动力学模型如下：
$$\begin{gathered} \dot{x}=v\cos \phi \\ \dot{y}=v\sin \phi \\ \dot{\phi }=\frac{v\tan {\delta }_f}{L} \end{gathered}$$
其中${\delta }_f$是前轮的转向角。因为后轮一般都是不转向的，所以${\delta }_r$是零。

2、动力学模型

需要考虑轮胎的侧偏性质。动力学模型是通过对轮胎和地面之间的相互作用来描述车辆的运动。动力学模型是基于车辆的动力学原理进行建模的，它考虑了车辆的质量、加速度、速度、转向等因素，可以更加精确地预测车辆的运动轨迹。动力学模型的优点在于可以考虑更多的因素，更加精确地预测车辆的运动轨迹，适用于高速行驶和紧急情况下的自动驾驶。但是，动力学模型对传感器的精度要求较高，对于复杂的路况和车辆之间的交互，需要更多的计算资源。

动力学模型可以将车辆运动的横纵向解耦，而运动学模型则无法解耦。

根据自行车动力学模型的推导，注意动力学模型中一个很关键的参数就是轮胎测偏参数，轮胎测偏力和轮胎测偏角度成正比。在实际中，测偏刚度是负数。

经过推导可以计算出关于横向速度和角速度作为状态变量，横向加速度和横向角速度变化量为因变量的状态方程。如下：
$$\left(\begin{array}{c}\ddot{y}\\ \ddot{\phi }\end{array}\right)=(\begin{array}{c}\frac{C_{{\phi }_f}+C_{{\phi }_r}}{m{v}_x}\\ \frac{a{C}_{{\phi }_f}-b{C}_{{\phi }_r}}{I{v}_x}\end{array}\begin{array}{c}\frac{a{C}_{{\phi }_f}+b{C}_{{\phi }_r}}{m{v}_x}-v_x\\ \frac{a^2{C}_{{\phi }_f}+b^2{C}_{{\phi }_r}}{I{v}_x}\end{array}$$