---

一、题目描述

你这个学期必须选修 numCourses 门课程，记为 0 到 numCourses - 1 。

在选修某些课程之前需要一些先修课程。 先修课程按数组 prerequisites 给出，其中 prerequisites[i] = [ai, bi] ，表示如果要学习课程 ai 则 必须 先学习课程 bi 。

例如，先修课程对 `[0, 1]` 表示：想要学习课程 `0` ，你需要先完成课程 `1` 。

请你判断是否可能完成所有课程的学习？如果可以，返回 true ；否则，返回 false 。

示例 1

输入：numCourses = 2, prerequisites = [[1,0]]
输出：true
解释：总共有 2 门课程。学习课程 1 之前，你需要完成课程 0 。这是可能的。

示例 2

输入：numCourses = 2, prerequisites = [[1,0],[0,1]]
输出：false
解释：总共有 2 门课程。学习课程 1 之前，你需要先完成​课程 0 ；并且学习课程 0 之前，你还应先完成课程 1 。这是不可能的。

提示：
1 <= numCourses <= 10^5
0 <= prerequisites.length <= 5000
prerequisites[i].length == 2
0 <= ai, bi < numCourses
prerequisites[i] 中的所有课程对 互不相同

二、代码

代码如下：

class Solution:
    def canFinish(self, numCourses: int, prerequisites: List[List[int]]) -> bool:
        nodes = [i for i in range(numCourses)]
        indegree = [0 for i in range(numCourses)]
        
        # 构建入度列表，记录每个node对应的入度值
        for i in range(len(prerequisites)):
            indegree[prerequisites[i][0]] += 1

        # 删除入度为0的node直到所有node均被删除
        while len(nodes) != 0:
            if 0 not in indegree:
                print("False")
                return False
            # 入度为0的节点对应的index和node值
            de_index = indegree.index(0)
            de_node = nodes[de_index]
            # 更新入度表
            for i in range(len(prerequisites)):
                if prerequisites[i][1] == de_node:
                    indegree[nodes.index(prerequisites[i][0])] -= 1
            # 删除该入度为0的node
            nodes.pop(de_index)
            indegree.pop(de_index)

        print("True")
        return True

---

三、解题思路

本题判断是否能够学完课程，实际上是判断课程学习的前后顺序是否冲突，我们可以将本题中有前后学习关联的课程看做是一个个节点，将它们都放置在一个图上，用箭头来表示其先后学习关系，则该图的每个节点的入度的含义是学习该门课程需要先学习的前置课程数量。
例如：
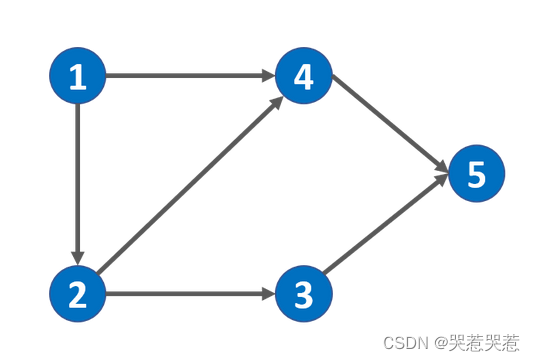我们在学习课程4时需要先学习课程1和课程2。课程4节点对应的入度为2，对应在prerequisites中的数组有2个，分别是[4,1]和[4,2]。
我们可以发现，想要学习完所有课程，则需要找到一定的学习顺序，这个学习顺序需要不违背图中箭头的前后关系。
所以本题的解题思路可以转化为：每次学习的目标选择节点入度为0的课程，然后删除该节点（表示已学习该课程），更新图中的节点和入度关系，直到所有节点都被删除，即所有课程都被1学习。