👨‍🎓作者简介：一位即将上大四，正专攻机器学习的保研er
🌌上期文章：机器学习&&深度学习——感知机
📚订阅专栏：机器学习&&深度学习
希望文章对你们有所帮助

上一节已经简单讲解了感知机，并且用XOR函数来举例说明单层感知机的不足，在这里进行多层感知机的讲解。

解决XOR

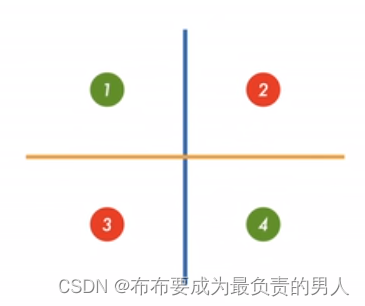
如上图所示，分别利用黄线和蓝线来对输入特征进行分别，并用表格来进行表示：

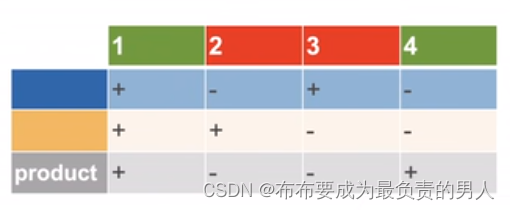
这个表格就直接很容易的体现出了输入和输出的关系，很明显这不是单层感知机能够完成的，而是需要进行如下的过程：

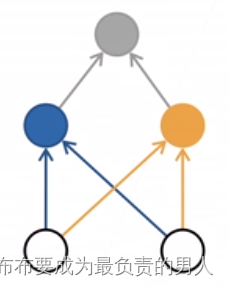
显然，我们要从白圈得到输入的值，从而得知黄圈和蓝圈分别是什么符号再得到灰色的输出值。
简单来讲，这就是一个单隐藏层，也就是说输入和输出之间隐藏了一层运算，单隐藏图如下图：

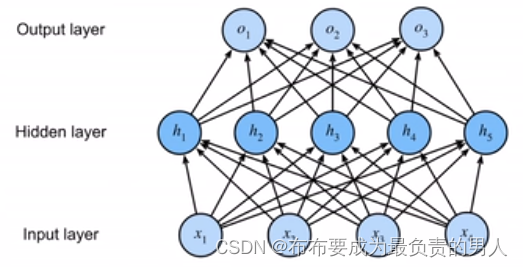
其中，隐藏层的大小是超参数。隐藏层的相关内容将在后面详细介绍。

隐藏层

对于之前的线性回归模型，标签通过仿射变换以后，确实与我们的输入数据直接相关了，所以无需隐藏层。但是，仿射变换中的线性其实是一种太过于强的假设了。

线性模型可能会出错

线性模型意味着单调：任何特征的增大都会导致模型输出的增大或缩小（取决于对应的权重符号）。
然而我们能找出很多违反单调性的例子。例如，我们想要根据体温预测死亡率。对体温高于37摄氏度的人来说，温度越高风险越大。然而，对体温低于37摄氏度的人来说，温度越高风险就越低。
再比如，上一节中我们对猫狗图像进行分类，如果用线性模型，区分猫和狗的唯一要求变为了评估单个像素的强度。在一个倒置图像后依然保留类别的世界里，注定失败。
这是因为，任何像素的重要性都以复杂的方式取决于该像素的上下文（周围像素的值）。由于这会考虑到特征之间的相关交互作用，所以我们引入了隐藏层。

在网络中加入隐藏层

我们可以在网络中加入一个或多个隐藏层来克服线性模型的限制，使其可以处理更普遍的函数关系类型。要做到这一点，最简单的方法是将许多全连接层都堆叠到一起，每一层都输出到上面的层，直到生成最后的输出。
我们可以把前L-1层都看作是表示，把最后一层看作是线性预测器。这种架构就叫做多层感知机，缩写为MLP

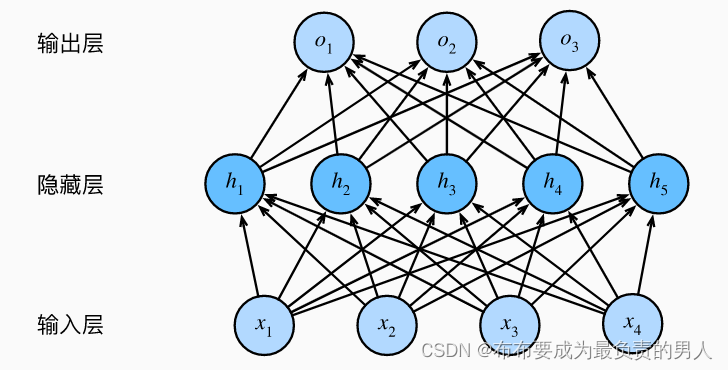
如该图为一个单隐藏层的多层感知机，具有5个隐藏单元。输入层不涉及任何计算，因此使用此网络产生输出只需要实现隐藏层和输出层的计算。
因此，该MLP的层数为2,。注意，这两个层都是全连接的，每个输入都会影响隐藏层的每个神经元，而隐藏层中的每个神经元又会影响输出层中的每个神经元。

从线性到非线性

我们通过矩阵X表示n个样本的小批量，其中每个样本都具有d个输入特征。对于具有h个隐藏单元的单隐藏层多层感知机，用H表示隐藏层的输出，称为隐藏表示。我们用如下方式计算单隐藏层多层感知机的输出O：
$$\begin{gathered} H=X{W}^{(1)}+b^{(1)} \\ O=H{W}^{(2)}+b^{(2)} \end{gathered}$$
其实，如果只是上面的式子，并没有改变线性模型的情况。我们试着合并一下单隐藏层，可得：
$$O=(X{W}^{(1)}+b^{(1)})W^{(2)}+b^{(2)}=X{W}^{(1)}{W}^{(2)}+b^{(1)}{W}^{(2)}+b^{(2)}$$
上式其实也只有X是未知的，那么上式其实就可以等价于O=XW+b了。
因此，为了发挥出多层架构的潜力，我们需要引入激活函数σ。激活函数的输出称为活性值。一般来说，只要有了激活函数，就不可能再将我们的多层感知机退化成线性模型：
$$\begin{gathered} H=\sigma (X{W}^{(1)}+b^{(1)}), \\ O=H{W}^{(2)}+b^{(2)} \end{gathered}$$

通用近似定理

多层感知机可以通过隐藏神经元，捕捉到输入之间复杂的相互作用，这些神经元依赖于每个输入的值。
我们可以很容易地设计隐藏结点从而执行任意计算。例如在一对输入上进行基本逻辑操作，多层感知机是通用近似器。即使是网络只有一个隐藏层，给足足够的神经元和正确的权重，我们可以对任意函数建模。
虽然一个单隐藏层可以学习任何函数，但是不代表通过一个单隐藏层就可以解决所有问题，事实上通过更深的网络，可以更容易的逼近许多函数。

激活函数

前面已经讲过了激活函数的必要性，它是线性模型转换为非线性模型的关键。激活函数通过计算加权和并加上偏置来确定神经元是否应该被激活，它们将输入信号转换为输出的可微运算。大多数激活函数都是非线性的。

import torch
from d2l import torch as d2l

ReLU函数

实现简单且最受欢迎的激活函数，就是修正线性单元（ReLU），它提供了一种非常简单的非线性变化：
$$ReLU(x)=max(x,0)$$
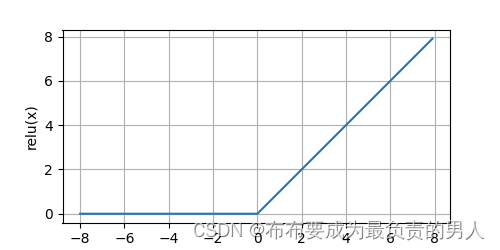
通俗的说，ReLU函数将对应的活性值设为0，仅保留正元素并丢弃所有负元素。我们可以画出函数的曲线图：

x = torch.arange(-8.0, 8.0, 0.1, requires_grad=True)
y = torch.relu(x)
d2l.plot(x.detach(), y.detach(), 'x', 'relu(x)', figsize=(5, 2.5))
d2l.plt.show()

我们可以绘制ReLU函数的导数：

y.backward(torch.ones_like(x), retain_graph=True)
d2l.plot(x.detach(), x.grad, 'x', 'grad of relu', figsize=(5, 2.5))
d2l.plt.show()

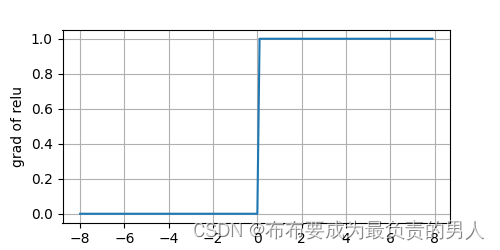
选用ReLU的原因：它求导表现的很好，要么让参数消失，要么让参数通过。这使得优化表现得更好，并且ReLU减轻了困扰以往神经网络的梯度消失问题。
而ReLU也有很多变体，如参数化ReLU函数，其添加了一个线性项，因此即使参数是负的，某些信息仍然可以通过：
$$pReLU(x)=max(0,x)+\alpha min(0,x)$$

sigmoid函数

sigmoid函数将输入变换为区间(0,1)上输出，因此通常称为挤压函数：
$$sigmoid(x)=\frac{1}{1+e^{-x}}$$

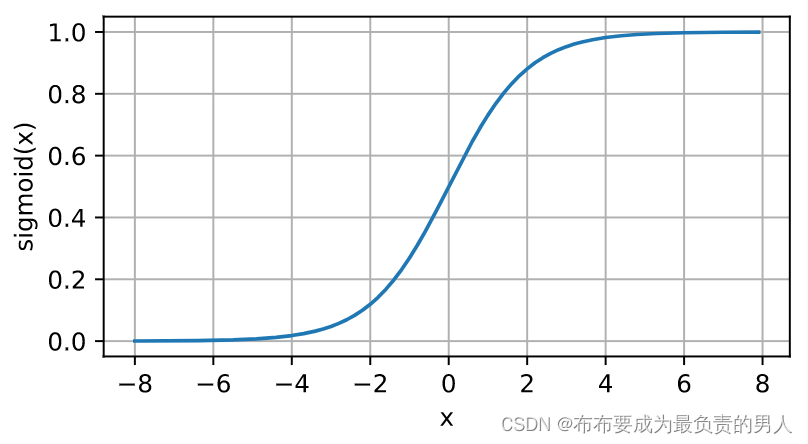
tanh函数

和sigmoid类型，双曲正切函数也是压缩区间，压缩到了(-1,1)：
$$tanh(x)=\frac{1-e^{-2x}}{1+e^{-2x}}$$

多类分类

其实就是之前的softmax函数加了个隐藏层：
$$\begin{gathered} 输入x\in R^n \\ 隐藏层W_1\in R^{m\times n},b_1\in R^m \\ 输出层W_2\in R^{m\times k},b_2\in R^k \end{gathered}$$
那么可以得到：
$$\begin{gathered} h=\sigma (W_{1}x+b_1) \\ o=W_2^{T}h+b_2 \\ y=softmax(o) \end{gathered}$$
注意这里的o的表达式和之前写的不一样，上面只是给出个大概，而真正要进行运算的时候要满足矩阵乘法的原则：前面的列数等于后面的行数。