01Two Sum - LeetCode
我自己写的代码【193ms】
因为不知道怎么加cmp函数,就只能pair的first设为值了,但其实这也是瞎做,应该也是O(n²)吧
class Solution {
public:
vector<int> twoSum(vector<int>& nums, int target) {
pair<int,int>pa[10004];int n=0;
for(auto i:nums){
pa[n].first=i;pa[n].second=n;n=n+1;
}
sort(pa,pa+n);
int j=0,i=1;
while(j<n){
if(pa[i].first+pa[j].first<target){
if(i!=n-1)i++;
else {j++;i=j+1;}
}
else if(pa[i].first+pa[j].first>target){
j++;i=j+1;
}
else return {pa[i].second,pa[j].second};
}
return {-1,-1};
}
};O(n²)代码【319ms】
class Solution {
public:
vector<int> twoSum(vector<int>& nums, int target) {
int n = nums.size();
for(int i = 0; i < n; i++)
for(int j = i + 1; j < n; j++)
if(nums[i] + nums[j] == target) return {i,j};
return {-1,-1};
}
};O(nlogn)代码【16ms】
我想到了排序,也想到了应该双指针,但没想到应该左指针在最左,右指针在最优
如果总和大于target,大的变小,如果总和小于target,小的变大。
class Solution {
public:
vector<int> twoSum(vector<int>& nums, int target) {
pair<int,int>pa[10004];int n=0;
for(auto i:nums){
pa[n].first=i;pa[n].second=n;n=n+1;
}
sort(pa,pa+n);
int j=0, i=n-1;
while(j<i){
int sum = pa[j].first+pa[i].first;
if(sum==target) return {pa[j].second, pa[i].second};
else if(sum>target) i--;
else j++;
}
return {-1,-1};
}
};O(n)代码【4ms】
用了Hash。原理是加入一个值,如果map里面有对应的值就输出各自的序号,没有就保存序号。蓝桥杯有一道题好像就是这样做的
class Solution {
public:
vector<int> twoSum(vector<int>& nums, int target) {
int n = nums.size();
unordered_map<int,int> mp;
for(int i=0;i<n;i++){
if(mp.count(target-nums[i])) return {i,mp[target-nums[i]]};
mp[nums[i]] = i;
}
return {-1,-1};
}
};02Add Two Numbers - LeetCode
一开始看错了,以为最右边是个位,看了一些答案才发现是最左边是个位
首先先创建一个头节点,之后有一个移动指针p->next=new ListNode(sum%10);
一直到链表遍历完,进位(carry)结束
最后返回链表head->next
我的代码
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
ListNode* head=new ListNode();
ListNode* p=head;
int carry=0;
while(l1!=NULL||l2!=NULL||carry){
int sum=0;
if(l1!=NULL){
sum+=l1->val;
l1=l1->next;
}
if(l2!=NULL){
sum+=l2->val;
l2=l2->next;
}
sum+=carry;
carry=sum/10;
p->next=new ListNode(sum%10);
p=p->next; //p指向下一个结点
}
return head->next;
}
};递归做法
class Solution {
public:
ListNode *helper(ListNode *l1,ListNode *l2,int carry){
if(!l1 && !l2){
if(carry) return new ListNode(carry);
else return NULL;
}
int val=(l1?l1->val:0)+(l2?l2->val:0)+carry;
ListNode *res=new ListNode(val%10);
res->next=helper((l1?l1->next:NULL),(l2?l2->next:NULL),val/10);
return res;
}
ListNode *addTwoNumbers(ListNode *l1,ListNode *l2){
return helper(l1,l2,0);
}
};03 Longest Substring Without Repeating Characters
有思路但不会写
我的思路
时间复杂度为n,就是直接扫一遍,每次扫到一个字符
如果vis为0,vis[i]设为1
如果扫到的vis已经为1,从头pop_front(),直到vis[i]为0,比较ans和max的大小,选择保留
之后,将扫到的字符加入ans中
困难
我发现string容器没有pop_front,而且每一次比较ans和max的大小,选择保留时都要重新遍历一遍,时间复杂度其实挺大的
答案思路
答案也用了vis,不过直接先把string存起来,记录pair下表
时隔几个星期后
之前的思路已经忘光光了,重新整理了思路,用vis记录string的下标,st的子串的左端点,string从1开始计数
若vis[s[i]]为真,那么将st到vis[s[i]]之间的字符的vis清零,st更新为vis[s[i]]+1,将vis[s[i]]更新为i;若vis[s[i]]为假,代表没遇到过这个字符,直接记录位置;
最后字符串循环一次后,记得再更新一次max的大小!!
另外初始化的时候,直接空字符串输出0!!
代码【11ms】
class Solution {
public:
int lengthOfLongestSubstring(string s) {
if(s=="")return 0;
if(s=="")return 0;
int vis[300]={0};pair<int,int>maxx;int st=1;maxx.first=1; maxx.second=1;
s="!"+s;
vis[s[st]]=st;
for(int i=2;i<s.size();i++){
if(vis[s[i]]){
if((i-st)>(maxx.second-maxx.first)){
maxx.first=st; maxx.second=i;
}
while(st<=vis[s[i]]){vis[s[st]]=0;st++;}//将st更新到重复出现的位置的后面
}
vis[s[i]]=i;//如果没有,记录位置;有就更新位置
}
if((s.size()-st)>(maxx.second-maxx.first)){
maxx.first=st; maxx.second=s.size();
}
return maxx.second-maxx.first;
}
};4. Median of Two Sorted Arrays
两个已排好序的数组 找中位数 数组从0开始计数
算法课上学过O(log(mn))的算法,但是忘记了,只会O(m+n)的合并后直接中位数了
代码【43ms Beats 62.01%】O(m+n)
class Solution {
public:
double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
vector<int>use;
int len1=nums1.size(),len2=nums2.size();
int i=0,j=0;
for(;i<len1&&j<len2;){
if(nums1[i]<nums2[j]){
use.push_back(nums1[i]);i++;
}
else {
use.push_back(nums2[j]);j++;
}
}
while(i<len1){use.push_back(nums1[i]);i++;}
while(j<len2){use.push_back(nums2[j]);j++;}
int len=use.size();
if(len%2==1){return use[len/2];}
return (use[len/2]+use[len/2-1])/2.0;
}
};看了解析后:
简述:用二分查找的思想做这道题。如果要更小的,把最大的那部分给删了;如果要更大的,把最小的那部分给删了
设A数组和B数组的中位数为AM和AM,其位置是AI和BI,为了找位置为K的数:
如果AI+BI小于K,说明AI和BI的位置小了,要大一点;
若AV小于BV,那么把【Astart,AI】的部分删掉,确保不会删掉第K位数;反之亦然。
如果AI+BI大于等于K,说明 Astart到AI 和 Bstart到BI (共AI+BI+2个数)中有位置为K的数;
若AV大于BV,那么把【AI,Aend】的部分删掉,确保不会删掉第K位数;反之亦然。
最后A或者B的Start>End,结束;若BStart>BEnd,最后返回A【k-BStart】,反之亦然

代码【35ms Beats 86.96%】 O(log(m*n))
注意数组的范围是【0, n.size()-1】!!!
class Solution {
public:
double findMedianSortedArrays(vector<int>& n, vector<int>& m) {
int num=int(n.size())+int(m.size());
if(num%2)
return q(n,m,num/2,0,n.size()-1,0,m.size()-1);
return (q(n,m,num/2,0,n.size()-1,0,m.size()-1)+q(n,m,num/2-1,0,n.size()-1,0,m.size()-1))/2.0;
}
double q(vector<int>& a,vector<int>& b,int k,int Astart,int Aend,int Bstart,int Bend){
if(Astart>Aend)return b[k-Astart];
if(Bstart>Bend)return a[k-Bstart];
int AIndex=(Astart+Aend)/2,BIndex=(Bstart+Bend)/2;
int aV=a[AIndex],bV=b[BIndex];
if(AIndex+BIndex<k){//删除小的部分
if(aV>bV)
return q(a,b,k,Astart,Aend,BIndex+1,Bend);
else
return q(a,b,k,AIndex+1,Aend,Bstart,Bend);
}
else{//删除大的部分
if(aV>bV)
return q(a,b,k,Astart,AIndex-1,Bstart,Bend);
else
return q(a,b,k,Astart,Aend,Bstart,BIndex-1);
}
return -1;
}
};还有一个做法是O(log(min(m,n))),但是我没有看懂,在实际运行的时候,是45ms,就很怪
!没看懂的代码
class Solution {
public:
double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
if (nums1.size() > nums2.size()) {
return findMedianSortedArrays(nums2, nums1);
}
int m = nums1.size(), n = nums2.size();
int left = 0, right = m;
while (left <= right) {
int partitionA = (left + right) / 2;
int partitionB = (m + n + 1) / 2 - partitionA;
int maxLeftA = (partitionA == 0) ? INT_MIN : nums1[partitionA - 1];
int minRightA = (partitionA == m) ? INT_MAX : nums1[partitionA];
int maxLeftB = (partitionB == 0) ? INT_MIN : nums2[partitionB - 1];
int minRightB = (partitionB == n) ? INT_MAX : nums2[partitionB];
if (maxLeftA <= minRightB && maxLeftB <= minRightA) {
if ((m + n) % 2 == 0) {
return (max(maxLeftA, maxLeftB) + min(minRightA, minRightB)) / 2.0;
} else {
return max(maxLeftA, maxLeftB);
}
} else if (maxLeftA > minRightB) {
right = partitionA - 1;
} else {
left = partitionA + 1;
}
}
return 0.0;
}
};5. Longest Palindromic Substring
题意:给一个字符串,找回文串
我知道这是马拉车问题,但是我不记得马拉车的代码怎么写了;好像哈希也可以做这种题目,但是我能想到的哈希也是的
我的思路
首先设回文串是单数,遍历一遍字符串,接着设回文串是双数,遍历一遍字符串,时间复杂度是
class Solution {
public:
string longestPalindrome(string s) {
string st="";
for(int i=0;i<s.size();i++){
int r=0;
for(r=0;r<=i;r++){
if(s[i-r]!=s[i+r])break;
}
r--;
if((int)st.size()<2*r+1){st="";for(int d=i-r,co=0;d<=i+r;d++)st+=s[d];}
r=0;
for(r=0;r<=i+1;r++){
if(s[i-r+1]!=s[i+r])break;
}
r--;
if((int)st.size()<2*r){st="";for(int d=i-r+1,co=0;d<=i+r;d++)st+=s[d];}
}
return st;
}
};查解析的时候看到又说区间动态规划做这道题的,动态规划已经完全不会了qwq
不过动态规划和我这个方法的时间复杂度居然差不多 哈哈
我看懂了!
首先每个字母是一个回文串,所以所有dp[0][i]=True,之后一个个排,差不多就是这意思,看代码肯定能看懂
代码【180ms】区间dp O(n^2)
class Solution {
public:
string longestPalindrome(string s) {
int n=s.size();
string ans="";ans+=s[0];
bool dp[1005][1005]={0};//字母最后一个的序号 里回文串长度(不包含最后一个字母的长度)
for(int i=0;i<1005;i++)dp[i][0]=1;
for(int i=1;i<n;i++){
for(int j=i-1;j>=0;j--){
if(s[i]==s[j]){
if(i-j==1||dp[i-1][i-j-2]){
dp[i][i-j]=1;
if((int)ans.size()<i-j+1){
ans="";for(int d=j;d<=i;d++)ans+=s[d];}
}
}
}
}
return ans;
}
};然后看到同样是O(n^2)的双指针法,但是不理解为什么能快那么多
同样是看了代码就知道怎么做的了
代码 【9ms Beats 95.99%】双指针法
直接黏贴了别人的代码
class Solution {
public:
string longestPalindrome(string s) {
int lenLP=1;
int startLP=0;
int n=s.length();
for(int i=0;i<n;i++){
int right=i; // initialize right to current index
while(right<n && s[i]==s[right]) right++; // while equal characters increment right
int left=i-1; // initialize left to current index - 1
while(left>=0 && right<n && s[left]==s[right]){
left--;
right++;
}
int len=(right-1)-(left+1)+1;
if(len>lenLP){
lenLP=len;
startLP=left+1;
}
}
return s.substr(startLP,lenLP);
}
};Manacher算法
算法思想
首先在首尾和每个数字之间添加”#“,例如”aofs“改成”“#a#o#f#s#”,这样解决了奇偶不同的问题,即字符串永远都是奇数,同时第0位,随便加上一个符号
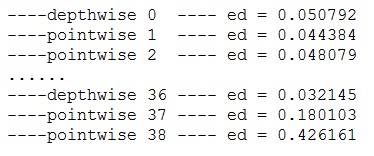
p表示包括当前字符的 加入#后的 回文串半径,例如
# a # a # c # a # b # d # k # a # c # a # a #
1 2 3 2 1 4 1 2 1 2 1 2 1 2 1 2 1 4 1 2 3 2 1
pos和maxlen表示答案的中心和长度
id和mx表示最右边的回文串的中心和端点,注意:mx不包含在回文串中
遍历字符串 t 时,如果此时在最右回文串的外面(或者i=1时,mx=0),即 i>mx,那么p[i]=1
若 i 在最右边的已知回文串区域的右端点里面,说明这个回文串左边镜像字符 2*id-i 已经求过p[i]了
如果 p[2*id-i]+i 大于mx,即p[2*id-i]大于mx-i,就暂定p[i]=mx-i,因为超出回文串了
如果p[2*id-i]+i 小于mx,即p[2*id-i]小于mx-i,因为还在回文串里面,所以p[i]=p[2*id-i]
在 t[i+p[i]] == t[i-p[i]] 的基础上,向外扩展、更新p[i]
如果出现了新的最右字符串,那么更新id和mx
代码【10ms Beats 95.49%】Manacher
居然和上面的双指针时间差不多 哈哈
class Solution {
public:
string longestPalindrome(string s) {
string t = "$#";
for(auto i : s){
t += i;
t += "#";
}
vector<int>p(t.size(),1);//包括当前字符的 加入#后的 回文串半径
int pos = 0;
int maxlen = 0;
int id = 0;
int mx = 0;
for(int i=1;i<t.size();i++){//遍历字符串
p[i] = i<mx?min(p[2*id-i],mx-i):1;
//i=0 或 i已经比最右边的已知回文串区域的右端点还要右, p[i]=1;
//若i在最右边的已知回文串区域的右端点里面,说明这个回文串左边镜像字符2*id-i已经求过p[i]了
//如果 p[2*id-i]+i 大于mx,即p[2*id-i]大于mx-i,就暂定p[i]=mx-i,因为超出回文串了
//如果p[2*id-i]+i 小于mx,即p[2*id-i]小于mx-i,因为还在回文串里面,所以p[i]=p[2*id-i]
while(t[i+p[i]] == t[i-p[i]]){
//当前位置i,已经知道当前的位置的p[i](p[i]是包括自己的)
p[i]++;//向外拓展来更新p[i]
}
if(i+p[i]>mx){//mx是最右边的已知回文串区域的右端点,不在回文串里面的第一个数字
mx = i+p[i];
id = i;//最右边的已知回文串中心
}
//记录最终的答案
if(p[i]>maxlen){
maxlen = p[i];
pos = i;
}
}
//(pos - maxlen)/2 长度
return s.substr( (pos - maxlen)/2,maxlen-1 );
}
};11. Container With Most Water
题意:求min(h[l] , h[r])*(r - l)最大
我的思路
双循环,O(n^2),但n=1e5 会超时,不会做不会做
双指针解析
参考:6.container-with-most-water(装最多水的容器
以序列最外面两条边形成的乘积为起始面积,找出两条边中较小的一条,索引加一(i++),找出一条更大的边来代替较小的边,以使得整个容器最大(可以看参考链接的图,更易于理解)
代码 自己写的 111ms Beats 35.18%
class Solution {
public:
int maxArea(vector<int>& h) {
int l=0,r=h.size()-1;
int maxx=0;
while(l<r){
maxx=max(maxx,min(h[l],h[r])*(r-l));
if(h[l]>h[r])r--;
else l++;
}
return maxx;
}
};上述代码中还有可以优化的地方,因为当 l 或 r 更新时,一定要找到更大的h[ l ]或者h[ r ],否则对答案无影响
代码修改后 92ms Beats 92.74%
class Solution {
public:
int maxArea(vector<int>& h) {
int l=0,r=h.size()-1;
int maxx=0,minh=9999999;
while(l<r){
minh=min(h[l],h[r]);
maxx=max(maxx,minh*(r-l));
while(l<r && h[r]<=minh)r--;
while(l<r && h[l]<=minh)l++;
}
return maxx;
}
};为什么可以连续的h[r]<=minh和h[l]<=minh?例如【8,88,8】答案为16,就算右边动了,变成了【8,16】,最小的高还是8,底宽还变小了,所以在底宽变小的前提下,一定要将minh提高才可以
13. Roman to Integer
题意:给一串字符串,写出代表的罗马数字
我的思路
普通的模拟
改成if…else……可以从7ms进化成3ms
代码 3ms Beats 97.3% 模拟
class Solution {
public:
int romanToInt(string s) {
int ans=0;
for(int i=0;i<s.size();i++){
if(s[i]=='I'&&i+1<s.size()){
if(s[i+1]=='V'){ans+=4;i++;continue;}
else if(s[i+1]=='X'){ans+=9;i++;continue;}
}
else if(s[i]=='X'&&i+1<s.size()){
if(s[i+1]=='L'){ans+=40;i++;continue;}
else if(s[i+1]=='C'){ans+=90;i++;continue;}
}
else if(s[i]=='C'&&i+1<s.size()){
if(s[i+1]=='D'){ans+=400;i++;continue;}
else if(s[i+1]=='M'){ans+=900;i++;continue;}
}
if(s[i]=='I')ans+=1;
else if(s[i]=='V')ans+=5;
else if(s[i]=='X')ans+=10;
else if(s[i]=='L')ans+=50;
else if(s[i]=='C')ans+=100;
else if(s[i]=='D')ans+=500;
else if(s[i]=='M')ans+=1000;
}
return ans;
}
};14. Longest Common Prefix
题意:给出前缀组Str,找到最长的字符串前缀
我的思路
用map把所有Str中的string的所有前缀都收集了,在收集过程中记录下最长的前缀
代码 232ms Beats 5.31%
class Solution {
public:
string longestCommonPrefix(vector<string>& strs) {
map <string,int> mp;
int mx=0;string a="";string tmp="";
for(int i=0;i<strs.size();i++){
tmp="";
for(int j=0;j<strs[i].size();j++){
tmp+=strs[i][j];
mp[tmp]+=1;
cout<<tmp<<" "<<mp[tmp]<<endl;
if(mp[tmp]==(int)strs.size()&&(int)tmp.size()>mx){
mx=(int)tmp.size();a=tmp;
}
}
}
return a;
}
};标答思路
看公共前缀就把字符串组排序,看最后和最前的公共字符前缀即可
代码 3ms Beats 89.36% 逻辑构造题
class Solution {
public:
string longestCommonPrefix(vector<string>& strs) {
string tmp="";
sort(strs.begin(),strs.end());
int first=0,last=(int)strs.size()-1;
for(int i=0;i<min(strs[first].size(),strs[last].size());i++){
if(strs[first][i]==strs[last][i])tmp+=strs[first][i];
else break;
}
return tmp;
}
};15. 3Sum
题意:给定一串数组,输出三个数,使得三个数的和为0
我的思路
O(n^2)组成pair组,存入pair的和,线性组,以后一一对照 总之全部用map实现
最后居然过了没想到的哈哈哈哈哈
代码 2999ms Beats 5.00%
class Solution {
public:
vector<vector<int>> threeSum(vector<int>& nums) {
vector<pair<int,int> > pr[200005];int n=nums.size();map<int,int> a;
set< vector<int>> ans;vector<vector<int>> aa;
for(int i=0;i<n;i++){
a[nums[i]]++;
}
for(auto i:a){
for(auto j:a){
if(i.first==j.first &&i.second<=1)continue;
int as=i.first+j.first;
if(as+100000<0||as+100000>200000)continue;
pr[as+100000].push_back({i.first,j.first});
}
}//把所有的和都放好了
for(auto i:a){
int id=100000-i.first;
if(!pr[id].empty()){//如果有对应的
for(int j=0;j<pr[id].size();j++){//核对每一个符合的pair
if(i.first!=pr[id][j].first&&i.first!=pr[id][j].second
||i.first==pr[id][j].first&&i.first!=pr[id][j].second&&i.second>1
||i.first!=pr[id][j].first&&i.first==pr[id][j].second&&i.second>1
||i.first==pr[id][j].first&&i.first==pr[id][j].second&&i.second>2
){//如果三个数的序号不一样
vector<int> a;a.push_back(i.first);
a.push_back(pr[id][j].first);a.push_back(pr[id][j].second);
sort(a.begin(),a.end());
ans.insert(a);
}
}
}
}
for (auto q:ans){aa.push_back(q);}
return aa;
}
};标答 双指针
首先将nums按大小排序,这样方便之后查找目标答案
顺序遍历nums,target就是-nums[i],设left是i+1,right是nums.size()-1,sum=nums[left] + nums[right]
如果sum<target,说明sum太小了,left向右移来增大sum;如果sum>target,说明sum太大了,left向左移来减小sum;
如果sum=target,那么刚好{nums[i], nums[left], nums[right]}加入vector中【还是排好序的】,因为适配的target的组合不止一个,所以移动left和right来跳过相同的数,之后接着查找,直到left>right停止
代码 113ms Beats 97.35% 双指针+排序
class Solution {
public:
vector<vector<int>> threeSum(vector<int>& nums) {
vector<vector<int>> result;
int n = nums.size();// Sort the array to use two-pointer approach
sort(nums.begin(), nums.end());
for (int i=0; i<n-2;++i) {
if (i>0 && nums[i] == nums[i - 1]) {
continue; // Skip duplicates for the first element
}
int target = -nums[i];
int left = i + 1;
int right = n - 1;
while (left < right) {
int sum = nums[left] + nums[right];
if (sum == target) {
result.push_back({nums[i], nums[left], nums[right]});
while (left < right && nums[left] == nums[left + 1])
left++; // Skip duplicates for the second element
left++;
while (left < right && nums[right] == nums[right - 1])
right--;
right--; // Skip duplicates for the third element
}
else if (sum < target) left++;
else right--;
}
}
return result;
}
};17. Letter Combinations of a Phone Number
我的思路
直接死算(?),用map一个个放,最后输出符合个数的
代码 5ms Beats 9.32%
class Solution {
public:
vector<string> letterCombinations(string digits) {
vector<string> result;
vector <string> mp;
vector<string> as={"abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};
int start=0,end=0;
for(int i=0;i<digits.size();i++){//输入的按钮
int id=(digits[i]-'0')-2;
if(i==0){//初始化
for(int j=0;j<as[id].size();j++) {
string tmp;tmp+=as[id][j];
mp.push_back(tmp);
}
start=end;end=as[id].size();
cout<<start<<" "<<end<<" "<<endl;
continue;
}
for (int i=start;i<end;i++){//增加
for(int j=0;j<as[id].size();j++){
string tmp;tmp=mp[i];
tmp+=as[id][j];
mp.push_back(tmp);
}
}
int st=end;end=end+(int)as[id].size()*(end-start);start=st;
}
for (int i=start;i<end;i++){
result.push_back(mp[i]);
}
return result;
}
};标答
普通的循环:用两个vector交替,另外上面代码的-2好像不太行
代码 0ms Beats 100% 循环
class Solution {
public:
vector<string> letterCombinations(string digits) {
if(digits.empty()) return{};
vector<string> as={"", "", "abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};
vector<string> output={""};
for (auto st:digits){//输入
vector<string> temp;
for(auto c: as[(st-'0')] ){//字母
for(auto t:output){
temp.push_back(t+c);
}
}
output.clear();
output=temp;
}
return output;
}
};代码 0ms 6.27mb Beats 97.65% 递归
在主函数中,首先如果digit的长度为0,那就返回空;规定好mapping后进入递归函数
在递归函数中,跳出的条件是index大于digit的长度,ans把一次的outpu加入,退出递归;在递归中,首先是循环(表示这个按键可以是什么字母)进入递归(index+1),出递归后把这个字母弹出,进入下次循环装上下个可能的字母
class Solution {
public:
void solve(string &digits,vector<string> &ans,string &output,int index,vector<string> &mapping)
{
if(index>=(int)digits.size()){
ans.push_back(output);
return;
}
int id=digits[index]-'0';
for(int i=0;i<(int)mapping[id].size();i++){
output.push_back(mapping[id][i]);
solve(digits,ans,output,index+1,mapping);
output.pop_back();
}
}
vector<string> letterCombinations(string digits) {
if(!(int)digits.size())return {};
int index=0;vector<string> ans;
string output="";
vector<string> mapping={"","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};
solve(digits,ans,output,index,mapping);
return ans;
}
};