every blog every motto: You can do more than you think.
https://blog.csdn.net/weixin_39190382?type=blog
0. 前言
cv2.moments() 矩特征
1. 正文
(1). 空间矩
- 零阶矩:m00
- 一阶矩:m10,m01
- 二阶矩:m20,m11,m02
- 三阶矩:m30,m21,m12,m03
m j i = ∑ x , y [ f ( x , y ) ⋅ x i ⋅ y i ] m_{ji} = \sum_{x,y} [f(x,y)·x^i·y^i] mji=x,y∑[f(x,y)⋅xi⋅yi]
说明: i+j的值等多少就是多少阶矩
(2). 中心矩
通过减去均值而获得的平移不变性。能够比较不同位置两个对象是否一致,中心矩具有平移不变形
- 二阶中心矩:mu20,mu11,mu02
- 三阶中心矩:mu30,mu21,mu12,mu03
m u j i = ∑ x , y ( f ( x , y ) ⋅ ( x − x ‾ ) ⋅ ( y − y ‾ ) ) mu_{ji} = \sum_{x,y} (f(x,y)·(x-\overline x)·(y-\overline y)) muji=x,y∑(f(x,y)⋅(x−x)⋅(y−y))
(3).归一化中心矩
通过除以物体总尺寸而获得缩放不变形。即有平移不变性,又有缩放不变形。
- 二阶Hu矩:nu20,nu11,nu02
- 三阶Hu矩:nu30,nu21,nu12,nu03
n u j i = m u j i m 00 ( i + j ) / 2 + 1 nu_{ji} = {mu_{ji} \over m_{00}^{(i+j)/2+1}} nuji=m00(i+j)/2+1muji
(4). Hu矩
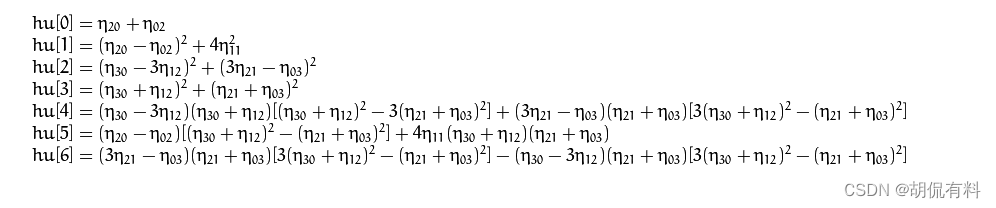
Hu矩具有尺度、旋转、平移不变性