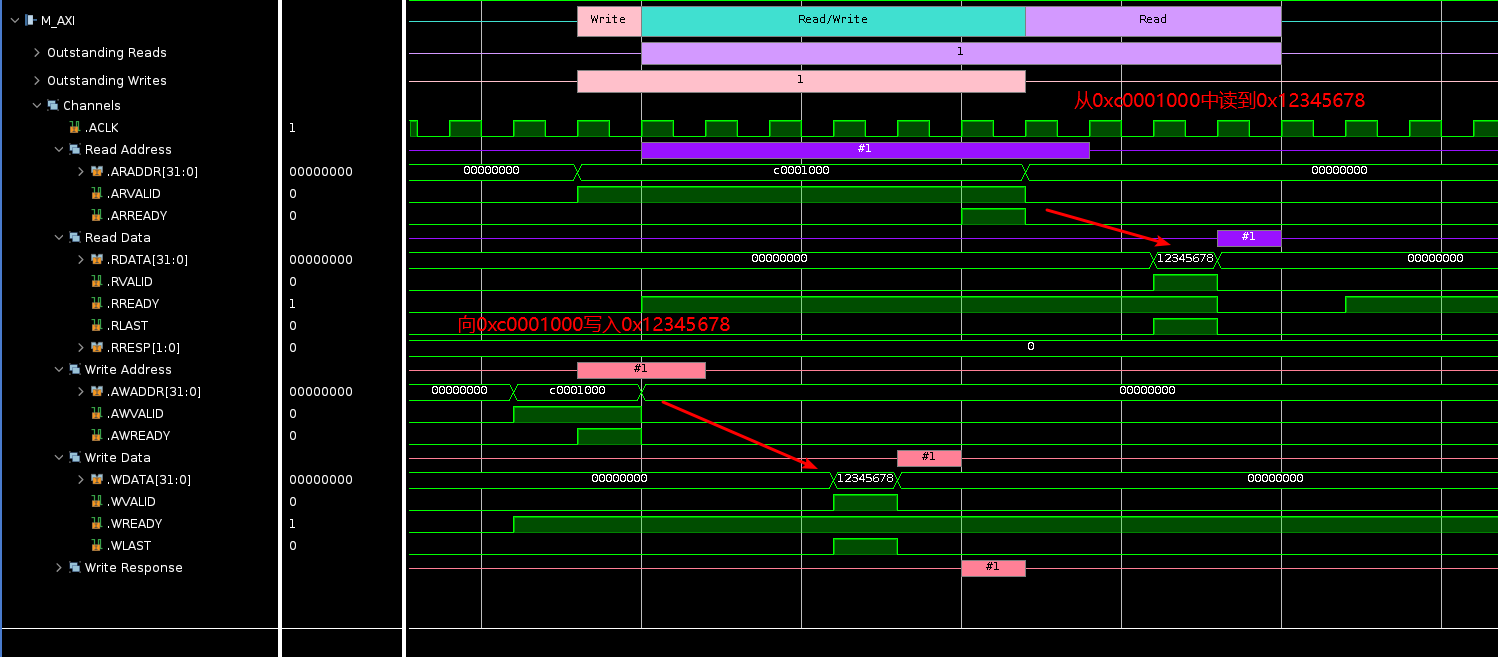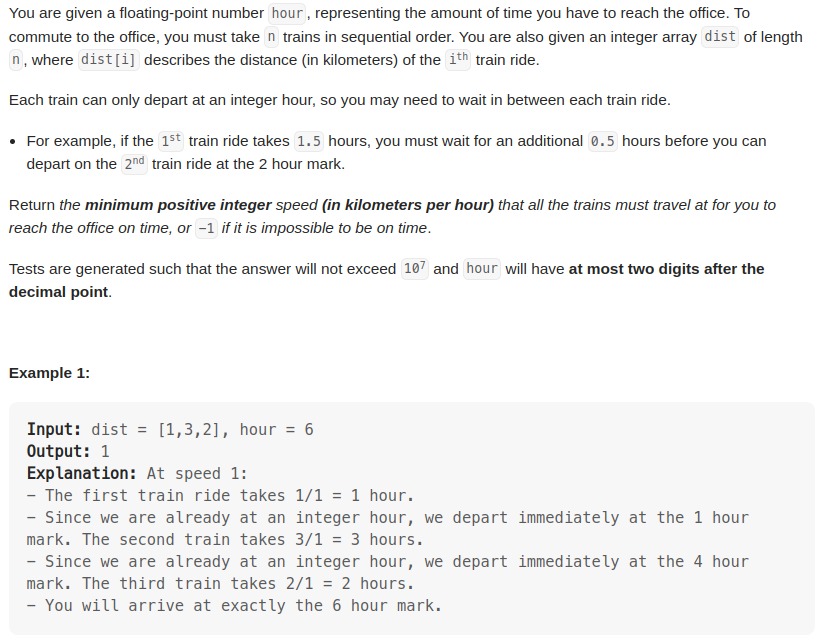
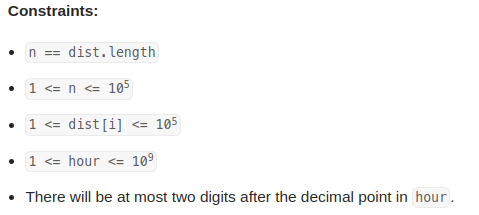
需要找一个speed, 使得dist[i] / speed 加起来的时间 <= hour,
而且如果前一个dist[i] / speed求出来的是小数，必须等到下一个整数时间才计算下一个。
speed最大不会超过10⁷.
不存在speed满足条件时返回-1.

思路：

如果前一个dist[i] / speed求出来的是小数，必须等到下一个整数时间才计算下一个。
也就是说在最后一个dist[n-1]之前的 dist[i]/speed都要取ceil.

speed不会超过10⁷,
也就是在1 ~ 10⁷范围内找到一个speed, 使得sum( ceil(dist[i]/speed)) (i=0~n-2) + dist[n-1]/speed <= hour.
可以想到binary search.

还有一种特殊的情况可以直接返回-1. 就是火车个数n特别大(转车次数多), 但是hour又不大的时候，不需要计算。
如何判断呢，当speed取最大值10⁷，dist[i]全都是最小值1，也就是每辆火车都嗖一下就到了，但是仍然无法在hour内到达的时候。
也就是说, 前n-1辆火车耗时n-1（前n-1个即使1/10⁷时间就到达，也要等1小时）,
最后一辆火车耗时10^-7, 总耗时n-1+10^-7仍然>hour时，直接返回-1.

    public int minSpeedOnTime(int[] dist, double hour) {
        if (dist.length -1 + 1e-7 > hour) {
            return -1;
        }
        int left = 1;
        int right = 10000001;

        while(left < right) {
            int mid = left + (right-left) / 2;
            if(cost(dist, mid) <= hour) {
                right=mid;
            } else {
                left = mid+1;
            }
        }
        return left == 10000001 ? -1 : left;
    }

    double cost(int[] dist, int speed) {
        double res = 0;
        int n = dist.length;
        for(int i = 0; i < n-1; i++) {
            res += (dist[i]+speed-1)/speed; //代替ceil运算,需要dist[i]和speed都是int
        }
        res += (double)dist[n-1]/speed;
        return res;
    }