LeetCode 63. 不同路径 II : https://leetcode.cn/problems/unique-paths-ii/

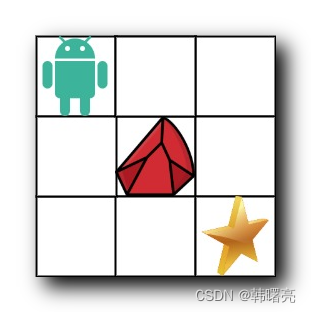
一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish”）。

现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？

网格中的障碍物和空位置分别用 1 和 0 来表示。

一、问题分析

---

在 m x n 的 二维坐标 网格中 , 出发位置是 ( 0 , 0 ) , 终点位置是 ( m - 1 , n - 1 ) ;

存在障碍物 : 网格中的某些节点存在障碍物 , 无法行走 ;

运动具有方向性 : 只能 向右 / 向下 行走 ;

上述问题 求的是 路径数 , 对应的是 动态规划 的 方案数 ,

将 大规模问题 拆解成 小规模问题 :

• ( i - 1 , j ) 位置是 ( i , j ) 位置 上面的点 , 从该点 向下走 1 步 , 即可走到 ( i , j ) 位置 ;
• ( i , j - 1 ) 位置是 ( i , j ) 位置 左边的点 , 从该点 向右走 1 步 , 即可走到 ( i , j ) 位置 ;

如果要走到 ( i , j ) 位置 , 只能是 从 ( i - 1 , j ) 位置 或 ( i , j - 1 ) 位置 过来 ;

大规模问题 与 小规模问题 的依赖关系 : 从 出发位置是 ( 0 , 0 ) 到 ( i , j ) 位置 的路径数 , 依赖于

• 从 出发位置是 ( 0 , 0 ) 到 ( i - 1 , j ) 位置 的路径数
• 从 出发位置是 ( 0 , 0 ) 到 ( i , j - 1 ) 位置 的路径数

该问题 与 【算法】动态规划 ③ ( LeetCode 62.不同路径 | 问题分析 | 自顶向下的动态规划 | 自底向上的动态规划 ) 博客问题的唯一区别就是 中间存在了 障碍物 ;

没有障碍时 ,

• 从 ( 0 , 0 ) 位置 走到 最左侧一列 位置的 方案数为 1 , 因为只能朝下面走 ;
• 从 ( 0 , 0 ) 位置 走到 最上面一行 位置的 方案数为 1 , 因为只能朝右侧走 ;

如果有障碍时 ,

• 如果障碍在第一列 , 则 从 ( 0 , 0 ) 位置 走到 最左侧一列 普通坐标时方案数为 1 , 如果 走到该列的 障碍位置的 方案数为 0 , 后面的坐标方案数都为 0 ;
• 如果障碍在第一行 , 则 从 ( 0 , 0 ) 位置 走到 最上面一行 普通坐标时方案数为 1 , 如果 走到该列的 障碍位置的 方案数为 0 , 后面的坐标方案数都为 0 ;

在计算时 ,

如果没有障碍 , 从 出发位置是 ( 0 , 0 ) 到 ( i , j ) 位置 的路径数 , 依赖于

• 从 出发位置是 ( 0 , 0 ) 到 ( i - 1 , j ) 位置 的路径数
• 从 出发位置是 ( 0 , 0 ) 到 ( i , j - 1 ) 位置 的路径数

如果遇到障碍 , 障碍位置的的方案数为 0 ;

二、动态规划算法设计

---

1、动态规划状态 State

使用 二维数组 dp 保存 动态规划的 状态 State ,

dp[i][j] 表示 从 (0, 0) 位置出发 , 到 (i, j) 位置的方案总数 ;

2、动态规划初始化 Initialize

动态规划初始化 Initialize :

• 如果障碍在第一列 , 则 从 ( 0 , 0 ) 位置 走到 最左侧一列 普通坐标时方案数为 1 , 如果 走到该列的 障碍位置的 方案数为 0 , 后面的坐标方案数都为 0 ;
• 如果障碍在第一行 , 则 从 ( 0 , 0 ) 位置 走到 最上面一行 普通坐标时方案数为 1 , 如果 走到该列的 障碍位置的 方案数为 0 , 后面的坐标方案数都为 0 ;

3、动态规划方程 Function

由于 运动时 , 只能 向右 或 向下 走 , 走到 (i , j) 只能是从 左边 (i - 1, j) 或 上边 (i , j-1) 位置走过来 ,

这里可以得到依赖关系 : dp[i][j] = dp[i-1][j] + dp[i][j-1]

如果遇到障碍物 , 则需要 continue 跳过本次计算 , 继续执行下一次计算 ;

4、动态规划答案 Answer

最终的 从 左上角 (0 , 0) 位置 走到 右下角 (m , n) 位置 的方案总数就是 状态 State 中的 dp[m - 1][n - 1] 数值 ;

三、代码示例

---

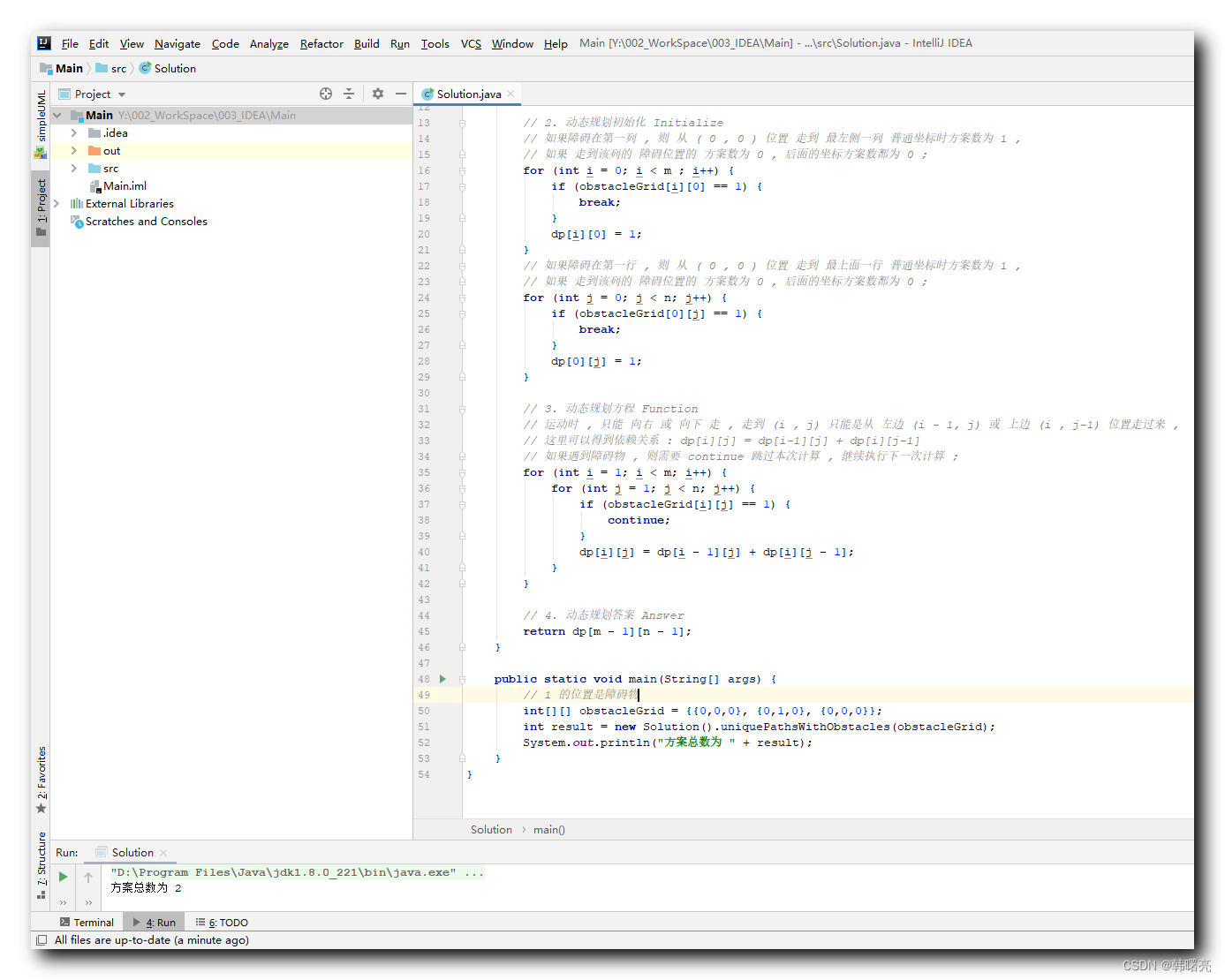
代码示例 :

class Solution {
    public int uniquePathsWithObstacles(int[][] obstacleGrid) {
        // 验证函数参数
        if (obstacleGrid == null || obstacleGrid.length == 0) {
            return 0;
        }

        // 1. 动态规划状态 State
        // dp[i][j] 表示 从 (0, 0) 位置出发 , 到 (i, j) 位置的方案总数 ;
        int m = obstacleGrid.length, n = obstacleGrid[0].length;
        int[][] dp = new int[m][n];

        // 2. 动态规划初始化 Initialize
        // 如果障碍在第一列 , 则 从 ( 0 , 0 ) 位置 走到 最左侧一列 普通坐标时方案数为 1 ,
        // 如果 走到该列的 障碍位置的 方案数为 0 , 后面的坐标方案数都为 0 ;
        for (int i = 0; i < m ; i++) {
            if (obstacleGrid[i][0] == 1) {
                break;
            }
            dp[i][0] = 1;
        }
        // 如果障碍在第一行 , 则 从 ( 0 , 0 ) 位置 走到 最上面一行 普通坐标时方案数为 1 ,
        // 如果 走到该列的 障碍位置的 方案数为 0 , 后面的坐标方案数都为 0 ;
        for (int j = 0; j < n; j++) {
            if (obstacleGrid[0][j] == 1) {
                break;
            }
            dp[0][j] = 1;
        }

        // 3. 动态规划方程 Function
        // 运动时 , 只能 向右 或 向下 走 , 走到 (i , j) 只能是从 左边 (i - 1, j) 或 上边 (i , j-1) 位置走过来 ,
        // 这里可以得到依赖关系 : dp[i][j] = dp[i-1][j] + dp[i][j-1]
        // 如果遇到障碍物 , 则需要 continue 跳过本次计算 , 继续执行下一次计算 ;
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                if (obstacleGrid[i][j] == 1) {
                    continue;
                }
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
            }
        }

        // 4. 动态规划答案 Answer
        return dp[m - 1][n - 1];
    }

    public static void main(String[] args) {
        // 1 的位置是障碍物
        int[][] obstacleGrid = {{0,0,0}, {0,1,0}, {0,0,0}};
        int result = new Solution().uniquePathsWithObstacles(obstacleGrid);
        System.out.println("方案总数为 " + result);
    }
}

执行结果 :

方案总数为 2