LeetCode 503.下一个更大元素II

链接：503.下一个更大元素II

思路：

本题其实和739. 每日温度更像一点，因为本题只有一个数组，而在下一个更大元素I中有两个，因此必须要一个哈希表来在另一个数组中查找相对应的数字。除此之外，本题由于是循环数组，所以在遍历的时候的查找范围也是不一样的，比如查找第i个元素的下一个更大元素，查找范围不仅仅是i之后的元素[i+1, nums.size() - 1]，还需要查找i前面的元素[0, i-1]。

首先将ans数组全部初始化为-1，然后遍历数组。考虑到数组是循环的，需要把[0, i-1]的元素再次放入栈里面，所以i的遍历次数为两倍的nums.size()，当i大于数组的长度后回到数组的开头，剩下的操作方法都是一致的，维持单调栈的单调递增的性质，当弹出元素的时候在ans里记录下是什么元素让它弹出的，最后返回ans即可。

代码：

class Solution {
public:
    vector<int> nextGreaterElements(vector<int>& nums) {
        vector<int> ans(nums.size(), -1);
        stack<int> st;
        for (int i = 0; i < nums.size() * 2; i++)
        {
            int idx = i >= nums.size() ? i-nums.size():i;
            while (!st.empty() && nums[st.top()] < nums[idx])
            {
                ans[st.top()] = nums[idx];
                st.pop();
            }
            st.push(idx);
        }
        return ans;
    }
};

LeetCode 42. 接雨水

链接：42. 接雨水

双指针

思路：

本题用双指针做的思路比较清晰，但是很容易超时。思路为遍历数组，数组每个元素代表一根柱子，目标为找到每个柱子上端能装的雨水量是多少，最后将所有柱子能装的雨水量累计起来，也就是按列计算。参考下面这张图：

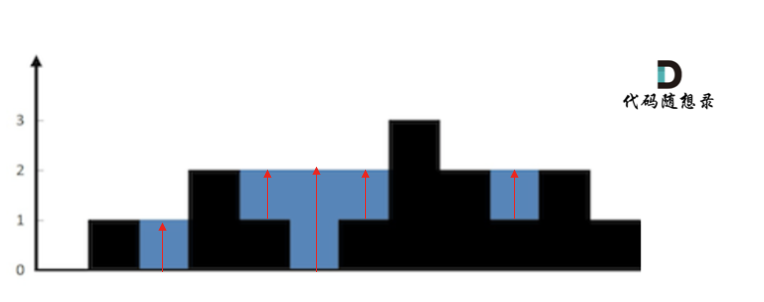
双指针的做法是，在遍历数组的时候，在每个元素i上用两个指针left和right，分别遍历i前面和后面所有的元素，找到左边和右边的最高柱子，再减去当前的高度height[i]，就是该柱子能装的雨水量。注意左右边的柱子不能低于当前柱子，否则会出现负数。

代码：

class Solution {
public:
    int trap(vector<int>& height) {
        int ans = 0;
        for (int i = 1; i < height.size() - 1; i++)
        {
            // 左边最高的
            int left = height[i];
            for (int leftIdx = i - 1; leftIdx >= 0; leftIdx--)
                if (left < height[leftIdx]) left = height[leftIdx];
            // 右边最高的
            int right = height[i];
            for (int rightIdx = i + 1; rightIdx < height.size(); rightIdx++)
                if (right < height[rightIdx]) right = height[rightIdx];
            ans += min(left, right) - height[i];
        }
        return ans;
    }
};

时间复杂度：O(n^2)

单调栈

思路：

由于双指针的做法时间复杂度是O(n^2)，不出以外的超时了。用单调栈可以在只遍历一遍数组的情况下做出这道题，只不过单调栈的思路很难理解。首先为了能接雨水，至少需要三根柱子，分别为两边的和中间的柱子。其次，两根的柱子一定要大于中间高度，利用单调栈，我们可以计算中间柱子上面的凹槽能储存的雨水量，按下图所示：

这次是按行来计算了。为了找到第一个大于当前元素的元素，单调栈还是使用从小到大的排法。计算每个由当前凹槽的长度和宽度决定。长度等于两根柱子的下标差，宽度等于边上两根较低的柱子的高度减去中间柱子的高度。

• width = i - st.top() - 1。i表示右边柱子的下标，st.top()表示左边柱子的下标
• height = min(height[st.top()], height[i]) - height[mid]。宽度为较低的柱子的高度减去中间柱子的高度。

首先按照单调栈的惯例，每次push元素进栈都要检查单调堆顶元素是否小于等于当前元素，如果当前元素大于等于堆顶元素，就需要将堆顶元素pop出来，此时堆顶元素表示中间柱子，当前元素为右边柱子，此时还需要检查左边柱子是否存在，如果左边柱子不存在则表示只有两根柱子，无法构成凹槽，如果存在，则根据公式计算凹槽的雨水量 ans += width * height。

代码：

class Solution {
public:
    int trap(vector<int>& height) {
        int ans = 0;
        stack<int> st;
        for (int i = 0; i < height.size(); i++)
        {
            // 检查单调堆顶元素是否小于等于当前元素
            while (!st.empty() && height[st.top()] <= height[i])
            {
                // 记录下中间柱子的高度
                int mid = st.top();
                // 先将中间柱子弹出，此时剩下的为左边柱子
                st.pop();
                // 必须确保左边柱子存在
                if (!st.empty())
                {
                    // 凹槽长度等于下标差，宽度等于两根柱子低的那个高度减去中间的高度
                    ans += (i - st.top() - 1) * (min(height[st.top()], height[i]) - height[mid]);
                }
            }
            st.push(i);
        }
        return ans;
    }
};