# coding: utf-8

## 感知器模型流程
"""
    1.初始化w, b
    2.遍历所有训练数据集中选出的误分类点：
        2.1.如果y != sign(wx+b) 或者 y*(wx+b) <= 0 则为误分类点
        2.2 根据误分类点计算：w_new = w_old -alpha * 对w的梯度， b_new = b_old - alpha * 对b的梯度
    3.直到没有误分类点或者达到迭代次数停止迭代.
"""

import sys
import numpy as np
import matplotlib.pyplot as plt

p_x = np.array([[4.0, 2.0], [3.0, 2.0], [2.5, 1.0], [2.0, 1.0]])
# print(p_x)
# sys.exit()
y = np.array([1, 1, -1, -1])

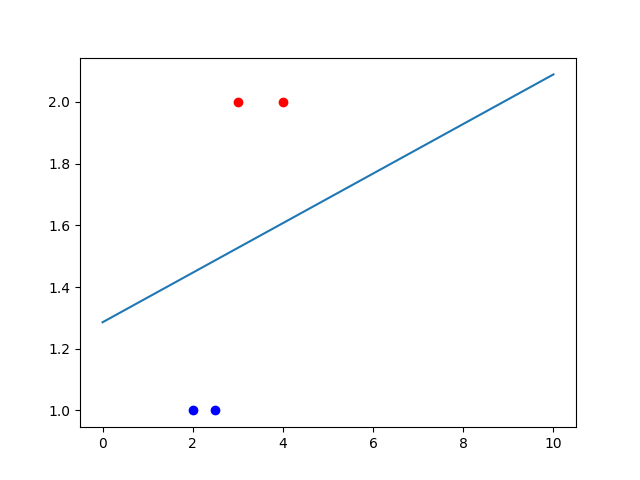
# 画出源数据点图分布
for i in range(len(p_x)):
    if y[i] == 1:
        # print(p_x[i][0], p_x[i][1])
        print(p_x[i])
        plt.plot(p_x[i][0], p_x[i][1], 'ro')
    else:
        plt.plot(p_x[i][0], p_x[i][1], 'bo')
# plt.show()
# sys.exit()

##找出分割超平面
# 初始化w,b
w = np.array([1.0, 1.0])
b = 1.0
# 设置初始学习率
alpha = 0.5
# 设置迭代次数
for i in range(160):
    # 选择误分类点
    choice = -1
    error_list = []
    for j in range(len(p_x)):
        # 判断误分类点
        if y[j] != np.sign(np.dot(w, p_x[0]) + b):
            choice = j
            error_list.append(j)
            ## 这里使用SGD，所以找到一个误分类点就可以更新一次,跳出当前for循环
            # break
        # if choice == -1:
        #     break
    if len(error_list) == 0:
        break
    for item in error_list:
        w += alpha * y[item] * p_x[item]
        b += alpha * y[item]
    # w = w + alpha * y[choice] * p_x[choice]
    # b = b + alpha * y[choice]
print(i)
print('w:{}\nb:{}'.format(w, b))

###画出超平面 w1*x1+w2*x2+b=0  ==>  x2=-(w1*x1+b)/w2
line_x = [0, 10]
line_y = [0, 0]
for i in range(len(line_x)):
    if w[1] != 0:
        line_y[i] = -(w[0]*line_x[i]+b)/w[1]
    else:
        line_x = [-b / w[0], -b / w[0]]
        line_y = [0, 1]
plt.plot(line_x, line_y)
plt.show()

E:\myprogram\anaconda\envs\python3.6\python.exe E:/XX/机器学习课程/L-SVM/svm.py
[4. 2.]
[3. 2.]
159
w:[-2.25 28.  ]
b:-36.0