梯度提升树的基本思想

1. 梯度提升树 VS AdaBoost

2. GradientBoosting回归与分类的实现

2.1 GradientBoosting回归

2.2 GradientBoosting分类

1. 梯度提升树 VS AdaBoost

梯度提升树（Gradient Boosting Decision Tree，GBDT）是提升法中的代表性算法，它即是当代强力的XGBoost、LGBM等算法的基石，也是工业界应用最多、在实际场景中表现最稳定的机器学习算法之一。在最初被提出来时，GBDT被写作梯度提升机器（Gradient Boosting Machine，GBM），它融合了Bagging与Boosting的思想、扬长避短，可以接受各类弱评估器作为输入，在后来弱评估器基本被定义为决策树后，才慢慢改名叫做梯度提升树。受Boosting算法首个发扬光大之作AdaBoost的启发，GBDT中自然也包含Boosting三要素：

① 损失函数𝐿(𝑥,𝑦)：用以衡量模型预测结果与真实结果的差异

② 弱评估器𝑓(𝑥)：（一般为）决策树，不同的boosting算法使用不同的建树过程

③ 综合集成结果𝐻(𝑥)：即集成算法具体如何输出集成结果

同时，GBDT也遵循boosting算法的基本流程进行建模：

        依据上一个弱评估器 $f(x)_{t-1}$ 的结果，计算损失函数 $L(x,y)$ ，
        并使用 $L(x,y)$ 自适应地影响下一个弱评估器 $f(x)_{t}$ 的构建。
        集成模型输出的结果，受到整体所有弱评估器 $f(x)_{0}$ ~ $f(x)_{T}$ 的影响。

但与AdaBoost不同的是，GBDT在整体建树过程中做出了以下几个关键的改变：

① 弱评估器

GBDT的弱评估器输出类型不再与整体集成算法输出类型一致。对于AdaBoost或随机森林算法来说，当集成算法执行的是回归任务时，弱评估器也是回归器，当集成算法执行分类任务时，弱评估器也是分类器。但对于GBDT而言，无论GBDT整体在执行回归/分类/排序任务，弱评估器一定是回归器。GBDT通过sigmoid或softmax函数输出具体的分类结果，但实际弱评估器一定是回归器。

② 损失函数𝐿(𝑥,𝑦)

在GBDT当中，损失函数范围不再局限于固定或单一的某个损失函数，而从数学原理上推广到了任意可微的函数。因此GBDT算法中可选的损失函数非常多，GBDT实际计算的数学过程也与损失函数的表达式无关。

③ 拟合残差

GBDT依然自适应调整弱评估器的构建，但却不像AdaBoost一样通过调整数据分布来间接影响后续弱评估器。相对的，GBDT通过修改后续弱评估器的拟合目标来直接影响后续弱评估器的结构。具体地来说，在AdaBoost当中，每次建立弱评估器之前需要修改样本权重，且用于建立弱评估器的是样本𝑋以及对应的𝑦，在GBDT当中，我们不修改样本权重，但每次用于建立弱评估器的是样本𝑋以及当下集成输出 $H(x_{i})$ 与真实标签𝑦的差异 $(y-H(x_{i}))$ 。这个差异在数学上被称之为残差（Residual），因此GBDT不修改样本权重，而是通过拟合残差来影响后续弱评估器结构。

④ 抽样思想

GBDT加入了随机森林中随机抽样的思想，在每次建树之前，允许对样本和特征进行抽样来增大弱评估器之间的独立性（也因此可以有袋外数据集）。虽然Boosting算法不会大规模地依赖于类似于Bagging的方式来降低方差，但由于Boosting算法的输出结果是弱评估器结果的加权求和，因此Boosting原则上也可以获得由“平均”带来的小方差红利。当弱评估器表现不太稳定时，采用与随机森林相似的方式可以进一步增加Boosting算法的稳定性。

除了以上四个改变之外，GBDT的求解流程与AdaBoost大致相同。sklearn当中集成了GBDT分类与GBDT回归，我们使用如下两个类来调用它们：

class sklearn.ensemble.GradientBoostingClassifier(*, loss='deviance', learning_rate=0.1, n_estimators=100, subsample=1.0, criterion='friedman_mse', min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_depth=3, min_impurity_decrease=0.0, init=None, random_state=None, max_features=None, verbose=0, max_leaf_nodes=None, warm_start=False, validation_fraction=0.1, n_iter_no_change=None, tol=0.0001, ccp_alpha=0.0)

class sklearn.ensemble.GradientBoostingRegressor(*, loss='squared_error', learning_rate=0.1, n_estimators=100, subsample=1.0, criterion='friedman_mse', min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_depth=3, min_impurity_decrease=0.0, init=None, random_state=None, max_features=None, alpha=0.9, verbose=0, max_leaf_nodes=None, warm_start=False, validation_fraction=0.1, n_iter_no_change=None, tol=0.0001, ccp_alpha=0.0)

比起AdaBoost，GBDT的超参数数量增加了不少，但与其他集成算法一样，GBDT回归器与GBDT分类器的超参数高度一致。

2. GradientBoosting回归与分类的实现

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.ensemble import GradientBoostingRegressor as GBR
from sklearn.ensemble import GradientBoostingClassifier as GBC
from sklearn.ensemble import AdaBoostRegressor as ABR
from sklearn.ensemble import RandomForestRegressor as RFR
from sklearn.model_selection import cross_validate, KFold
data = pd.read_csv(r"F:\\Jupyter Files\\机器学习进阶\\datasets\\House Price\\train_encode.csv",index_col=0)

def RMSE(result,name):
    return abs(result[name].mean())

2.1 GradientBoosting回归

梯度提升回归树：

#回归数据
X = data.iloc[:,:-1]
y = data.iloc[:,-1]
gbr = GBR(random_state=1412) #实例化
cv = KFold(n_splits=5,shuffle=True,random_state=1412) #定义所需的交叉验证方式
result_gbdt = cross_validate(gbr,X,y,cv=cv
                             ,scoring="neg_root_mean_squared_error" #负根均方误差
                             ,return_train_score=True
                             ,verbose=True)
RMSE(result_gbdt,"train_score") #13990.790813889864
RMSE(result_gbdt,"test_score") #28783.954343252786

梯度提升回归与其它算法的对比

import time
modelname = ["GBDT","RF","AdaBoost","RF-TPE","Ada-TPE"]

models = [GBR(random_state=1412)
         ,RFR(random_state=1412)
         ,ABR(random_state=1412)
         ,RFR(n_estimators=89, max_depth=22, max_features=14, min_impurity_decrease=0
              ,random_state=1412, verbose=False)
         ,ABR(n_estimators=39, learning_rate=0.94,loss="exponential"
              ,random_state=1412)]

colors = ["green","gray","orange","red","blue"]

for name,model in zip(modelname,models):
    start = time.time()
    result = cross_validate(model,X,y,cv=cv,scoring="neg_root_mean_squared_error"
                            ,return_train_score=True
                            ,verbose=False)
    end = time.time()-start
    print(name)
    print("\t train_score:{:.3f}".format(RMSE(result,"train_score")))
    print("\t test_score:{:.3f}".format(RMSE(result,"test_score")))
    print("\t time:{:.2f}s".format(end))
    print("\n")

------------------------------------------------------------------------------
GBDT
	 train_score:13990.791
	 test_score:28783.954
	 time:2.54s


RF
	 train_score:11177.272
	 test_score:30571.267
	 time:6.65s


AdaBoost
	 train_score:27062.107
	 test_score:35345.931
	 time:1.20s


RF-TPE
	 train_score:11208.818
	 test_score:28346.673
	 time:1.54s


Ada-TPE
	 train_score:27401.542
	 test_score:35169.730
	 time:0.86s

算法	RF	AdaBoost	GBDT	RF (TPE)	AdaBoost (TPE)
5折验证运行时间	6.65s	1.20s	2.54s	1.54s	0.86s
最优分数 (RMSE)	30571.267	35345.931	28783.954	28346.673	35169.730

首先来看默认参数下所有算法的表现。当不进行调参时，随机森林的运行时间最长、AdaBoost最快，GBDT居中，但考虑到AdaBoost的n_estimators参数的默认值为50，而GBDT和随机森林的n_estimators默认值都为100，可以认为AdaBoost的运行速度与GBDT相差不多。从结果来看，未调参状态下GBDT的结果是最好的，其结果甚至与经过TPE精密调参后的随机森林结果相差不多，而AdaBoost经过调参后没有太多改变，可以说AdaBoost极其缺乏调参空间、并且学习能力严重不足。

基于以上信息，我们可以观察三个算法的过拟合情况：

xaxis = range(1,6)
plt.figure(figsize=(8,6),dpi=80)

for name,model,color in zip(modelname[:3],models[:3],colors[:3]):
    result = cross_validate(model,X,y,cv=cv,scoring="neg_root_mean_squared_error"
                            ,return_train_score=True
                            ,verbose=False)
    plt.plot(xaxis,abs(result["train_score"]), color=color, label = name+"_Train")
    plt.plot(xaxis,abs(result["test_score"]), color=color, linestyle="--",label = name+"_Test")

plt.xticks([1,2,3,4,5])
plt.xlabel("CVcounts",fontsize=16)
plt.ylabel("RMSE",fontsize=16)
plt.title("RF vs GBDT vs AdaBoost")
plt.legend()
plt.show()

不难发现，AdaBoost是过拟合程度最轻的，这也反映出它没有调参空间的事实，而GBDT与随机森林过拟合程度差不多，不过GBDT的过拟合程度相对较轻一些，这是因为Boosting算法的原理决定了Boosting算法更加不容易过拟合。

绘制随机森林调参前后、以及AdaBoost调参前后的结果对比：

xaxis = range(1,6)
plt.figure(figsize=(8,6),dpi=80)

for name,model,color in zip(modelname[2:5:2],models[2:5:2],colors[2:5:2]):
    result = cross_validate(model,X,y,cv=cv,scoring="neg_root_mean_squared_error"
                            ,return_train_score=True
                            ,verbose=False)
    plt.plot(xaxis,abs(result["train_score"]), color=color, label = name+"_Train")
    plt.plot(xaxis,abs(result["test_score"]), color=color, linestyle="--",label = name+"_Test")

plt.xticks([1,2,3,4,5])
plt.xlabel("CVcounts",fontsize=16)
plt.ylabel("RMSE",fontsize=16)
plt.title("AdaBoost vs AdaBoost-TPE")
plt.legend()
plt.show()

xaxis = range(1,6)
plt.figure(figsize=(8,6),dpi=80)

for name,model,color in zip(modelname[1:4:2],models[1:4:2],colors[1:4:2]):
    result = cross_validate(model,X,y,cv=cv,scoring="neg_root_mean_squared_error"
                            ,return_train_score=True
                            ,verbose=False)
    plt.plot(xaxis,abs(result["train_score"]), color=color, label = name+"_Train")
    plt.plot(xaxis,abs(result["test_score"]), color=color, linestyle="--",label = name+"_Test")

plt.xticks([1,2,3,4,5])
plt.xlabel("CVcounts",fontsize=16)
plt.ylabel("RMSE",fontsize=16)
plt.title("RF vs RF-TPE")
plt.legend()
plt.show()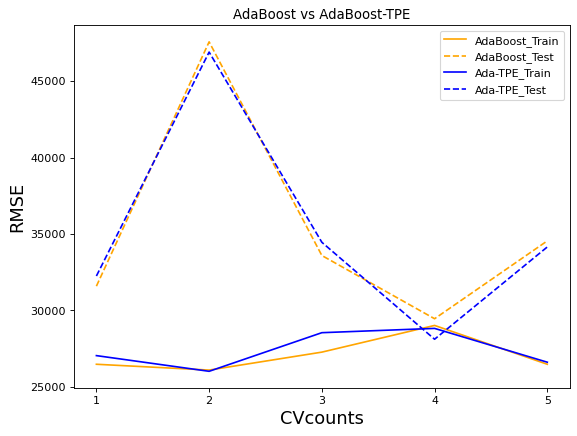

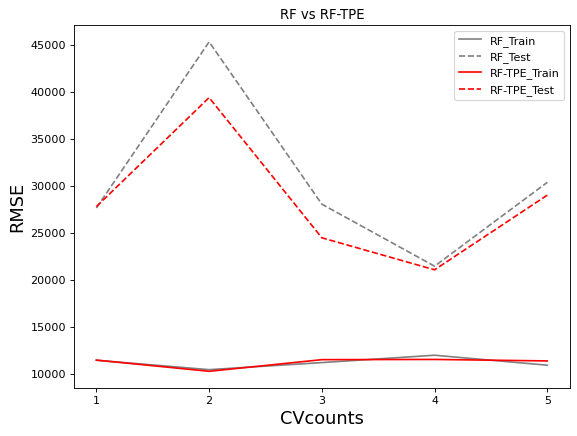
AdaBoost在经过精密调参后，并没有太多改变，而随机森林调参后过拟合程度明显降低，测试集上的结果明显提升，这是随机森林在潜力和根本原则上都比AdaBoost要强大的表现。

GBDT在默认参数上的结果接近经过TPE调参后的随机森林，我们来看看这两个算法的对比：

xaxis = range(1,6)
plt.figure(figsize=(8,6),dpi=80)

for name,model,color in zip(modelname[:5:3],models[:5:3],colors[:5:3]):
    result = cross_validate(model,X,y,cv=cv,scoring="neg_root_mean_squared_error"
                            ,return_train_score=True
                            ,verbose=False
                            ,n_jobs=-1)
    plt.plot(xaxis,abs(result["train_score"]), color=color, label = name+"_Train")
    plt.plot(xaxis,abs(result["test_score"]), color=color, linestyle="--",label = name+"_Test")

plt.xticks([1,2,3,4,5])
plt.xlabel("CVcounts",fontsize=16)
plt.ylabel("RMSE",fontsize=16)
plt.title("GBDT vs RF-TPE")
plt.legend()
plt.show()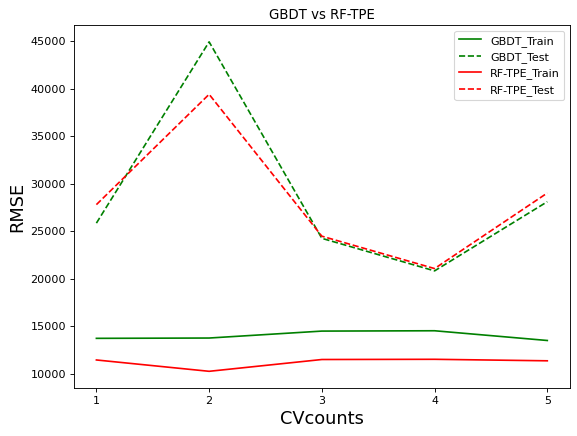

不难发现，GBDT的过拟合程度是轻于优化后的随机森林的。并且，在大部分交叉验证的结果下，GBDT的效果都接近或好于优化后的随机森林。在cv=2时GBDT的表现远不如森林，一次糟糕的表现拉低了GBDT的整体表现，否则GBDT可能在默认参数上表现出比优化后的随机森林更好的结果。如果我们可以通过调参优化让GBDT的表现更加稳定，GBDT可能会出现惊人的表现。

2.2 GradientBoosting分类

#分类数据
X_clf = data.iloc[:,:-2]
y_clf = data.iloc[:,-2]
np.unique(y_clf) #6分类
-----------------------------------------
array([0., 1., 2., 3., 4., 5.])

#GBDT分类的实现
clf = GBC(random_state=1412) #实例化
cv = KFold(n_splits=5,shuffle=True,random_state=1412)
result_clf = cross_validate(clf,X_clf,y_clf,cv=cv
                            ,return_train_score=True
                            ,verbose=True)
result_clf
----------------------------------------------------------
{'fit_time': array([3.47425294, 3.40723777, 3.38023067, 3.39023256, 3.41823983]),
 'score_time': array([0.0040009 , 0.00400043, 0.00400066, 0.00300074, 0.00400186]),
 'test_score': array([0.89726027, 0.8869863 , 0.90410959, 0.8869863 , 0.90753425]),
 'train_score': array([0.99058219, 0.99315068, 0.99229452, 0.99143836, 0.99143836])}

# 准确率
result_clf["train_score"].mean()  # 0.9917808219178083
result_clf["test_score"].mean()   # 0.8965753424657535