文章目录
- 一、974. 和可被 K 整除的子数组
- 1.题目简介
- 2.解题思路
- 3.代码
- 4.运行结果
- 二、525. 连续数组
- 1.题目简介
- 2.解题思路
- 3.代码
- 4.运行结果
- 三、560. 和为 K 的子数组
- 1.题目简介
- 2.解题思路
- 3.代码
- 4.运行结果
- 总结
一、974. 和可被 K 整除的子数组
1.题目简介
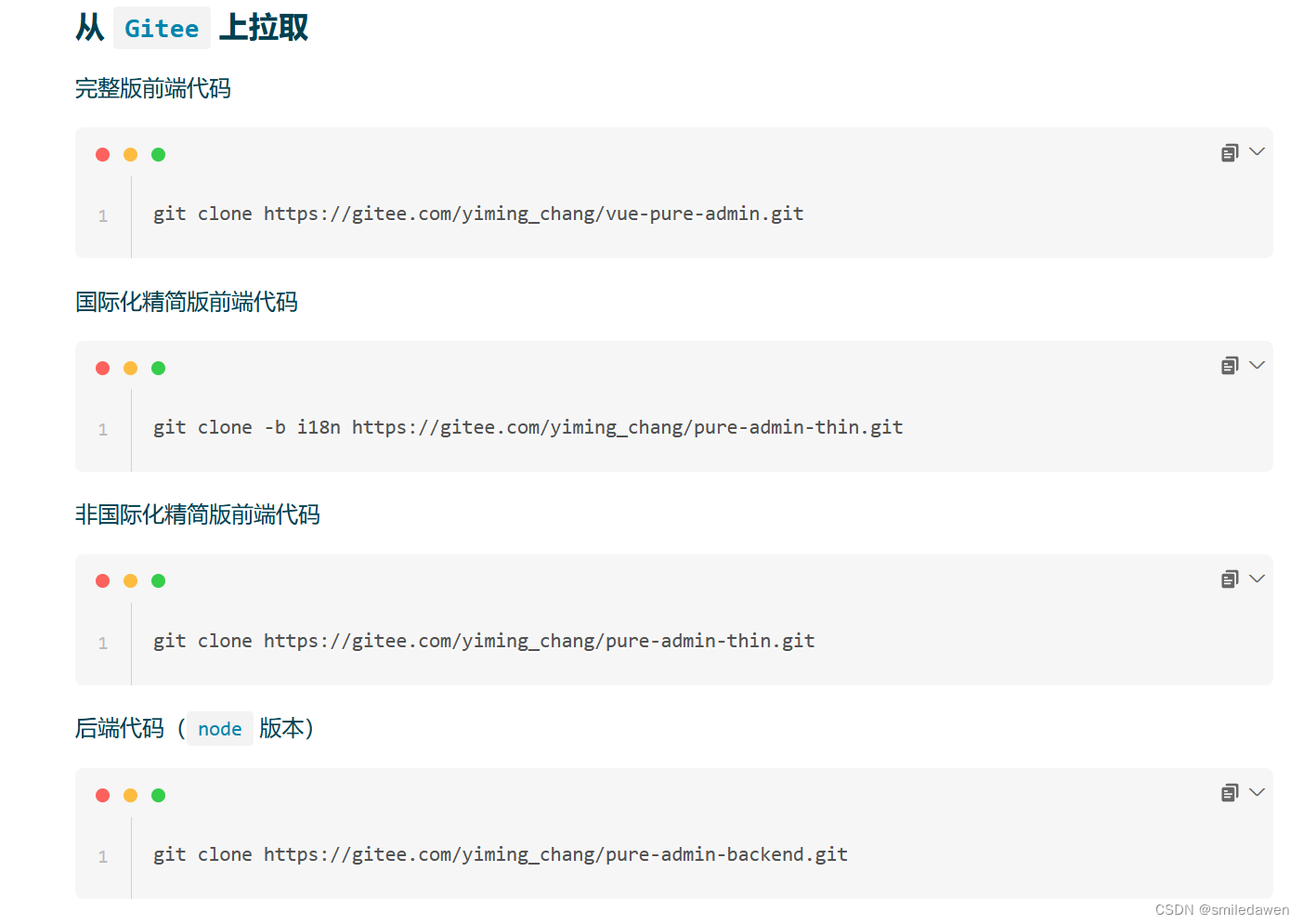
974. 和可被 K 整除的子数组
给定一个整数数组 nums 和一个整数 k ,返回其中元素之和可被 k 整除的(连续、非空) 子数组 的数目(子数组 是数组的 连续 部分)。


2.解题思路
3.代码
class Solution {
public:
int subarraysDivByK(vector<int>& nums, int k) {
//(sum[i] - sum[x]) % k == 0 => sum[i] % k == sum[x] % k;
unordered_map<int, int> ma;//存储至今为止的前缀和对k取余的结果出现的次数
ma[0 % k] = 1;
int sum = 0;
int ret = 0;
for(int i = 0;i < nums.size(); ++i)
{
sum += nums[i];
int t = (sum % k + k) % k;//修正负数取模的结果。C++对负数的取模机制会导致结果出错(先去掉负数的符号,然后将它当中一个正数进行取模,最后再带上符号)
if(ma.count(t)) ret += ma[t];
ma[t]++;
}
return ret;
}
};
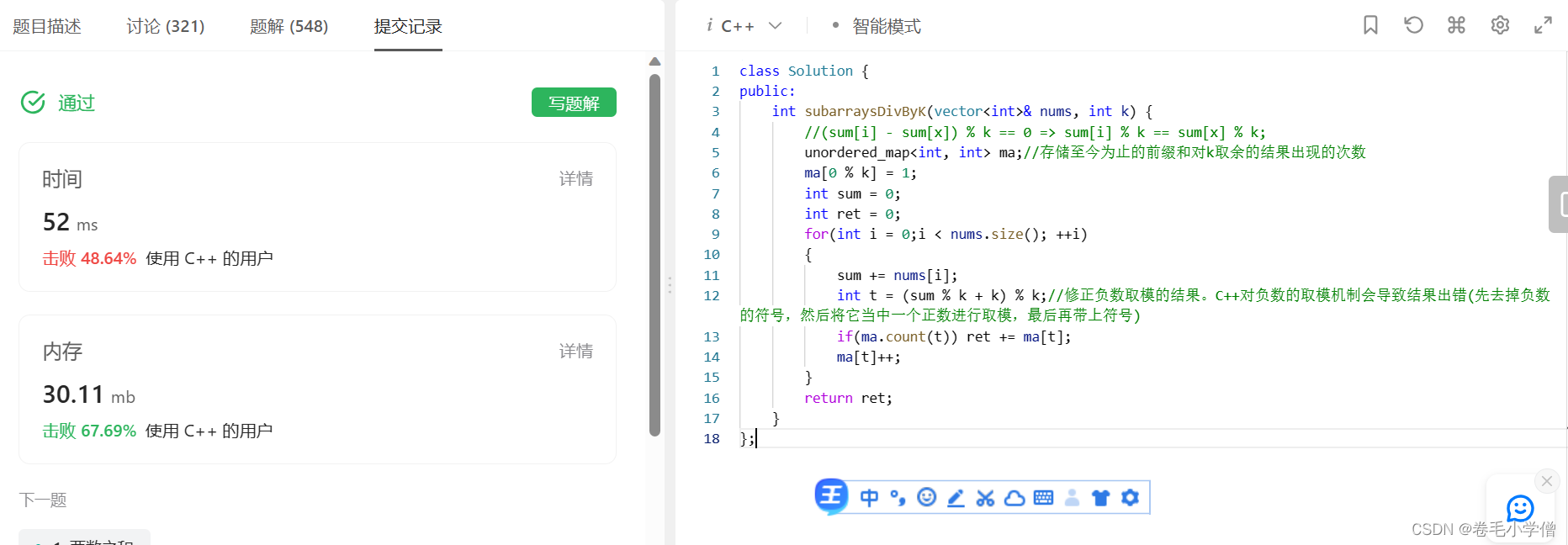
4.运行结果
二、525. 连续数组
1.题目简介
525. 连续数组
给定一个二进制数组 nums , 找到含有相同数量的 0 和 1 的最长连续子数组,并返回该子数组的长度。

2.解题思路
3.代码
class Solution {
public:
int findMaxLength(vector<int>& nums) {
map<int, int> ma;//存放至今为止出现的前缀和以及第一次出现该sum的下标
ma[0] = -1;//默认有一个前缀和为0的情况
for(auto& e : nums)
{
if(e == 0) e = -1;
}
//将数组中的0转化为-1,这样问题就转变为和为0的最长连续子数组,推测为找和为sum的最短连续子数组
int sum = 0;
int ret = 0;
for(int i = 0;i < nums.size(); ++i)
{
sum += nums[i];
if(ma.count(sum))
{
ret = max(ret, i - ma[sum]);
}
else
ma[sum] = i;
}
return ret;
}
};
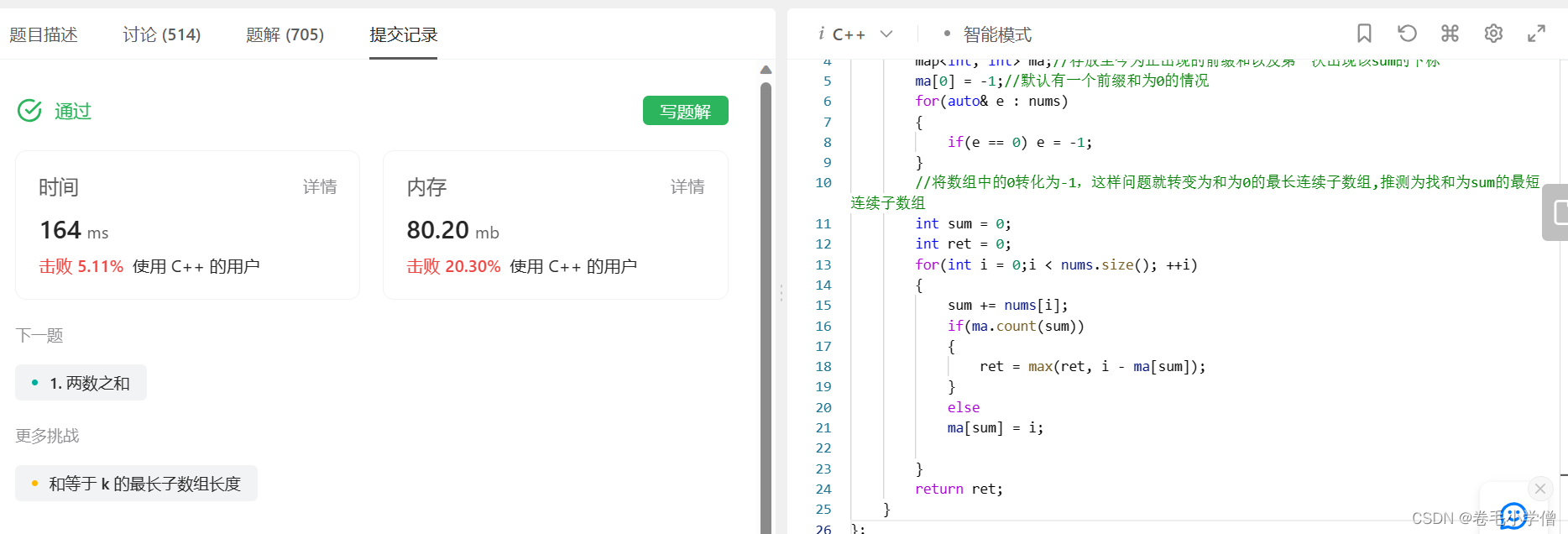
4.运行结果
三、560. 和为 K 的子数组
1.题目简介
560. 和为 K 的子数组
给你一个整数数组 nums 和一个整数 k ,请你统计并返回 该数组中和为 k 的连续子数组的个数 。

2.解题思路
3.代码
class Solution {
public:
int subarraySum(vector<int>& nums, int k) {
unordered_map<int, int> ma;//至今为止前缀和出现的次数
ma[0] = 1;//初始化(前缀和正好等于k的情况)
int ret = 0;
int sum = 0;//前缀和
for(int i = 0;i < nums.size(); ++i)
{
sum += nums[i];
int t = sum - k;
if(ma.count(t)) ret += ma[t];
ma[sum]++;
}
return ret;
}
};
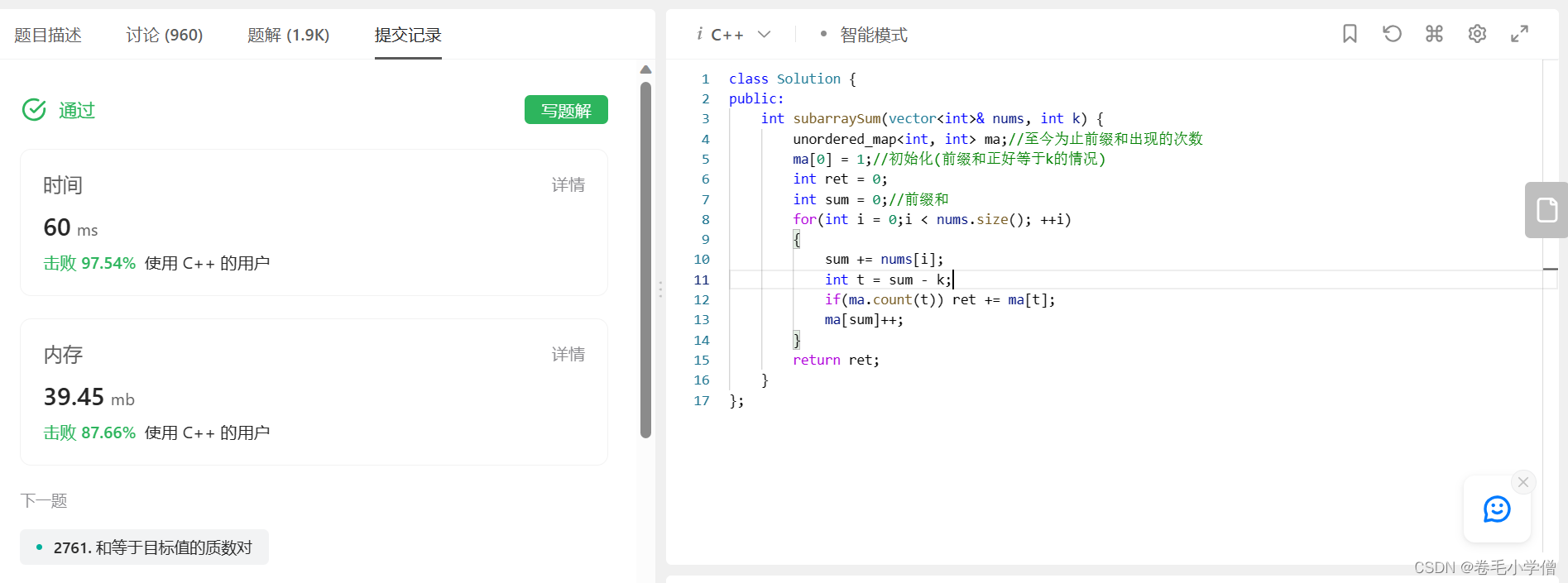
4.运行结果
总结
今天是算法练习的第8天。
故以往之不谏,知来者之可追。继续加油,决不放弃。
如果本篇文章对你有所启发的话,希望可以多多支持作者,谢谢大家!