本专栏是网易云课堂人工智能课程《神经网络与深度学习》的学习笔记,视频由网易云课堂与 deeplearning.ai 联合出品,主讲人是吴恩达 Andrew Ng 教授。感兴趣的网友可以观看网易云课堂的视频进行深入学习,视频的链接如下:
神经网络和深度学习 - 网易云课堂
也欢迎对神经网络与深度学习感兴趣的网友一起交流 ~
目录
1 指数加权平均
2 动量梯度下降法
1 指数加权平均
在介绍更复杂的优化算法之前,你需要了解指数加权平均(Exponentially Weighted Average),在统计学中也叫做指数加权移动平均(Exponentially Weighted Moving Average)。
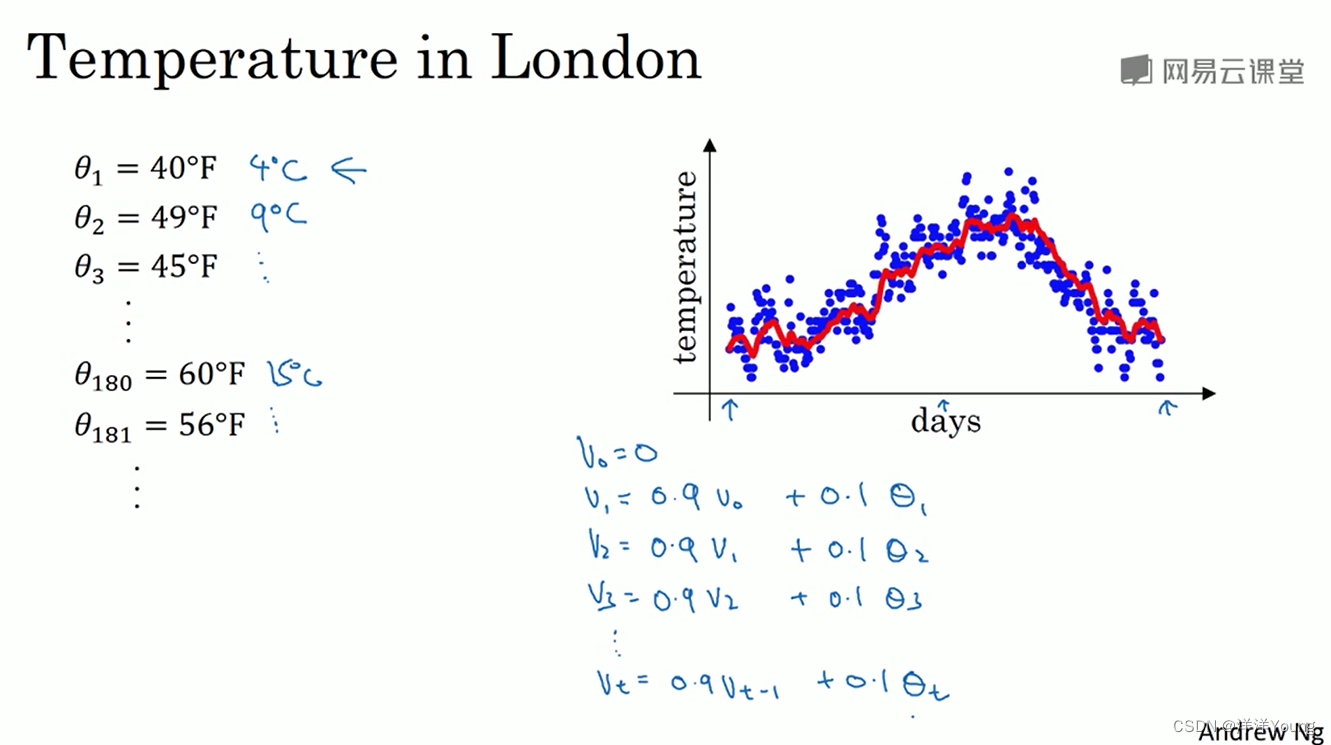
这里有伦敦一年的温度数据,如果想知道这一年温度的变化趋势,或者说温度的局部平均值,可以使用 0.9 乘以前一天的平均值,加上 0.1 乘以这一天的温度值,作为新的平均值。
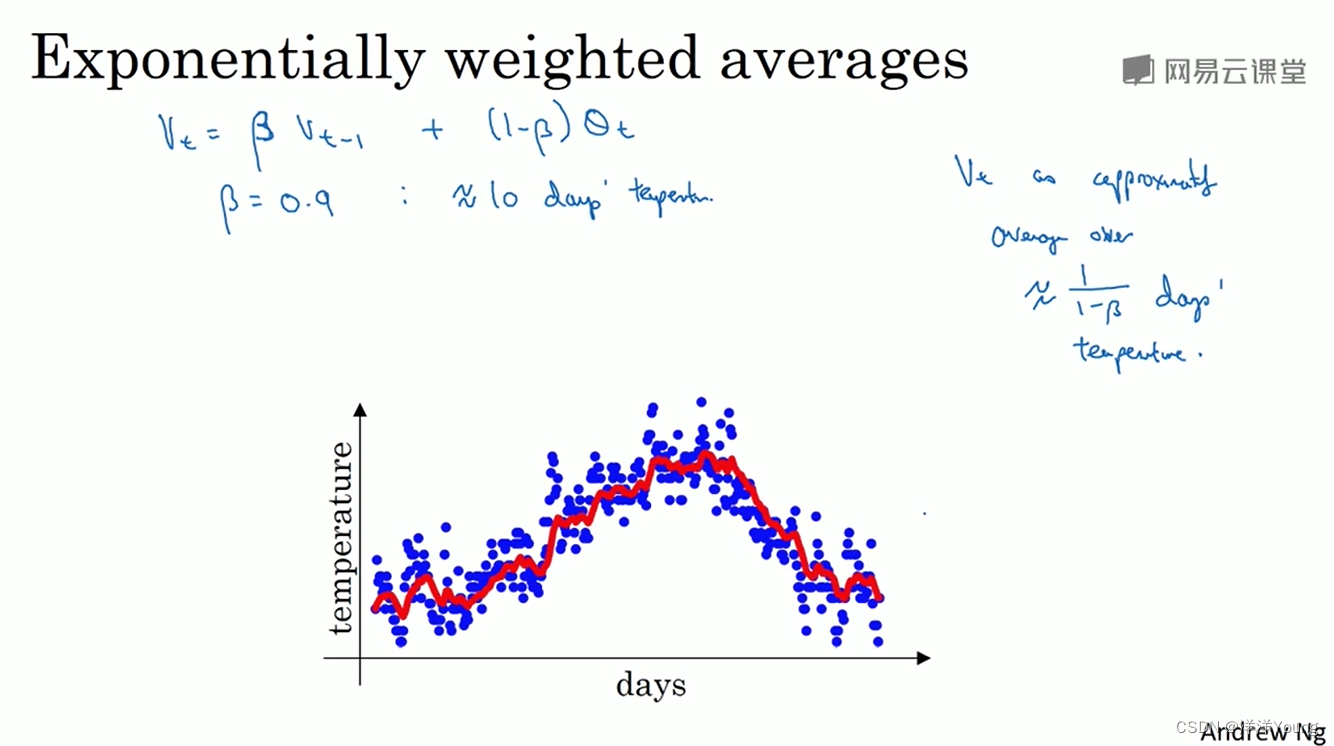
如果把系数 0.9 替换为 β,0.1 替换为 1-β,就得到指数加权平均的公式。
vt 可以解释为 1/(1-β) 天的平均值,例如 β 取 0.9,1/(1-β) = 10,vt 近似等于 10 天的温度平均值。

β 值越大,得到的曲线越平滑,例如上图中绿色的曲线(对应 β = 0.98)。因为前一天的温度权重为 0.98,当天的温度权重仅为 1 - 0.98 = 0.02,在温度变化时,平均值的变化越迟缓。
2 动量梯度下降法

假设上图中,红点代表成本函数最小值的位置,在标准的梯度下降算法迭代过程中,梯度缓慢地摆动到最小值,上下波动的趋势减慢了梯度下降法的速度。使用更大的学习率,波动可能更大,但是减小学习率,迭代的过程也会变慢。

使用动量梯度下降法(Momentum Gradient Descent),你需要做的是,计算梯度的指数加权平均值,然后用该值更新权重。

与 α 一样,这里 β 也是梯度下降算法中的一个超参数,你需要尝试不同的 β 值,然后根据结果选择最优的一个。