一.栈的基本概念
栈是一种特殊的表,这种表只在表首进行插入和删除操作。
因此,表首对于栈来说具有特殊的意义,称为栈顶。相应的,表尾称为栈底。不含任何元素的栈称为空栈。
栈的修改遵循后进先出的原则,Last In First Out,可以想象成一个水桶。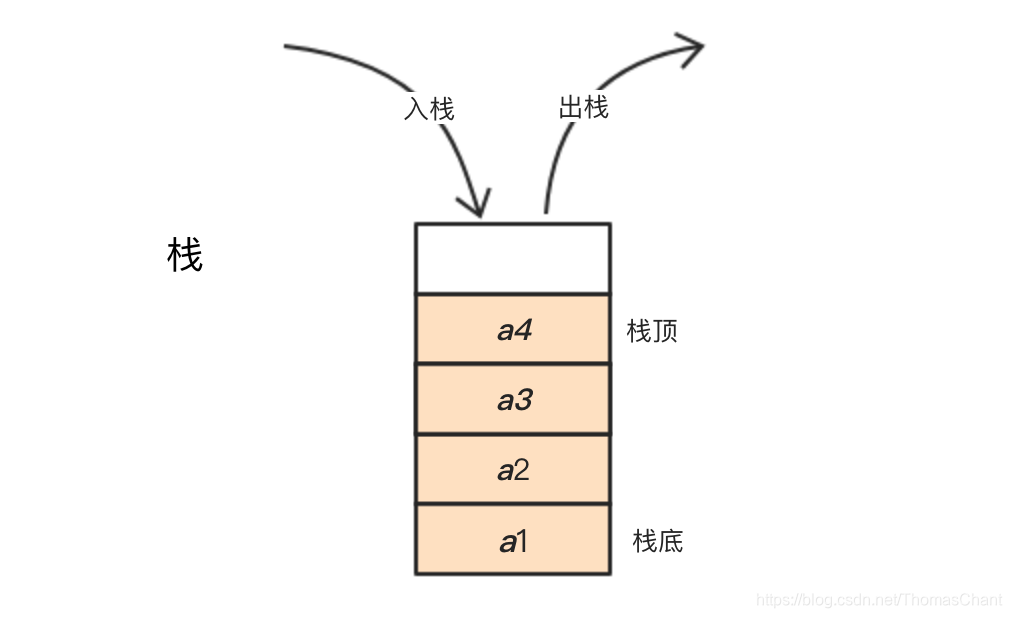
二.常用的栈运算
栈也是一个抽象数据类型。常用的栈运算如下:
(1)StackEmpty(S):测试栈S是否为空
(2)StackFull(S):测试栈S是否以满
(3)StackTop(S):返回栈S的栈顶元素
(4)Push(x,S):在栈S的栈顶插入元素x,简称为将元素x入栈
(5)Pop(S):删除并返回栈S的栈顶元素,简称为抛栈
三.栈的实现
1.用数组实现栈
实现与表类似,只不过要实现的运算不同。略
2.用指针实现栈
用这种方法实现的栈也叫做链栈。
因为栈是一种特殊的表,所以实现与表类似,只不过要实现的运算不同。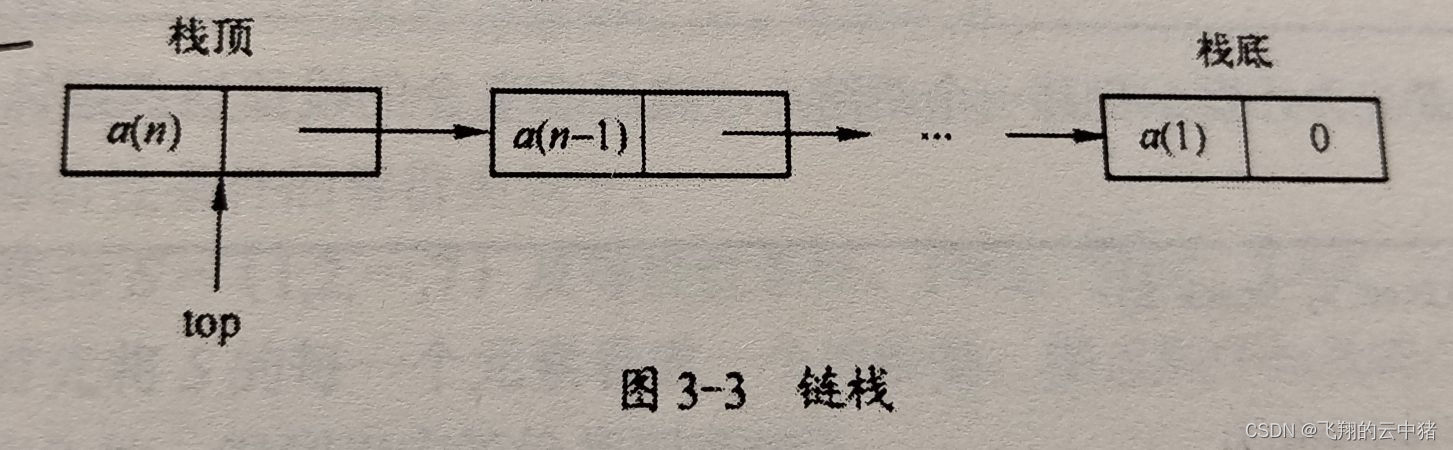
四.栈的应用
例一:在对用高级语言编写的程序进行编译时会遇到表达式或字符串的括号匹配问题。
在从左到右逐个字符对给定的表达式expr进行扫描的过程中,将所遇到的左括号存入一个栈中。每当扫描到一个有括号时,如果栈非空,就将其与栈顶的左括号想匹配,并从栈顶删除该左括号;若栈已空,则所遇到的右括号不匹配。在完成对表达式的扫描后,若栈非空,则留在栈中的左括号均不匹配。
例二:直方图最大面积矩形问题--单调栈
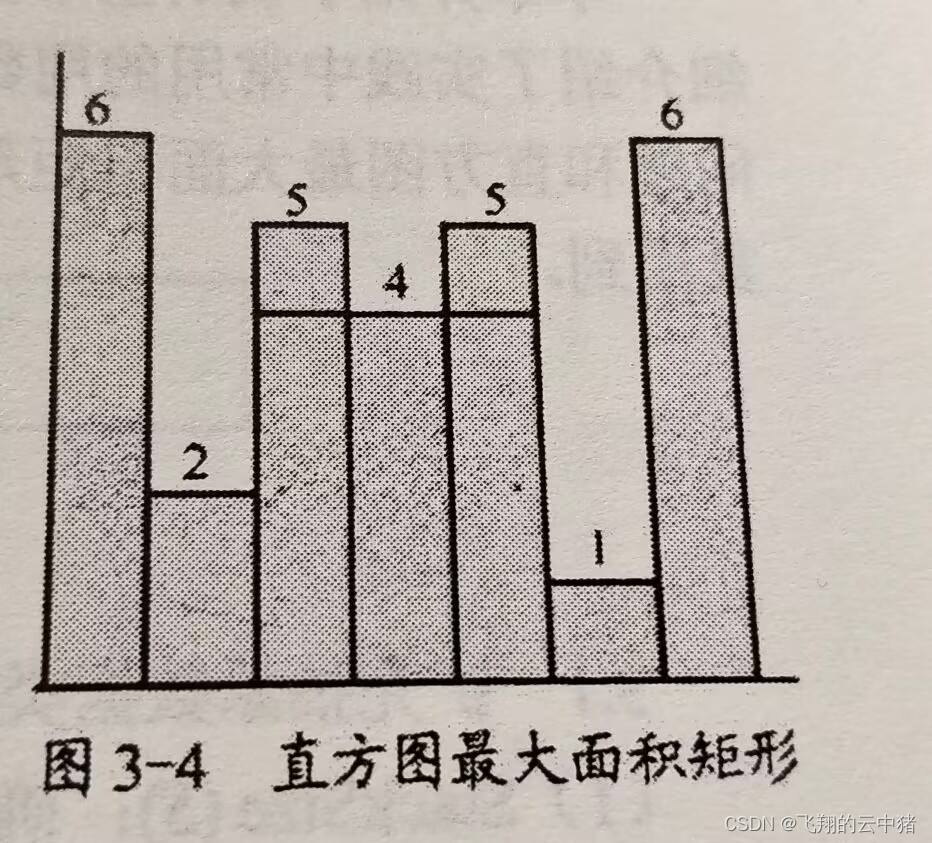
直方图最大面积矩形问题要找出包含在这个直方图中边平行于坐标轴的最大面积矩形。每个直条的宽度均为1。如上,当给出的h=[6,2,5,4,5,1,6]时,最大面积矩形的面积是12。
设最大面积矩形为s,则易知与其相交的直条中高度最小的直条整个包含在s中。而对直方图中的每个高度为h[i]的直条i都有一个包含该直条的最大矩形,设其面积为a[i]。显而易见,直方图最大面积矩形s的面积是当i取1到n的a[i]中的最大值。因此,关键问题是对每个高度为h[i]的直条i,计算包含该直条的最大矩形a[i]。(化归转化)
要计算a[i],就要计算直条i的左侧距i最近的高度小于h[i]的直条位置l(i),和直条i的右侧距i最近的高度小于h[i]的直条位置r(i)。由l(i)和r(i)的值可得,a[i]=h[i]*(r(i)-l(i)-1)。为此目的,可以用一个栈stk来存储直条i的位置l(i)。从左到右依次考察直条,并根据栈顶元素的值来计算a[i]。
int histo() {
//首先,创建一个栈 stk,并初始化为空栈。
Stack stk=StackInit(n);
//定义变量 i 和 max,分别表示遍历直方图数组的索引和最大矩形面积。
int i=0,max=0;
//进入循环,循环条件是 i < n,即遍历直方图数组,遍历的直方图遇到比它大的栈顶,栈顶弹出,直到遇到比它小的才入栈。
while(i<n) {
//在循环内部,首先检查栈是否为空或者当前直方图高度大于等于栈顶元素所对应的高度。
//如果满足条件,则将当前索引 i 入栈,并将 i 加 1。
if(StackEmpty(stk)||h[StackTop(stk)]<=h[i])
Push(i++,stk);
//如果不满足条件,说明当前直方图高度小于栈顶元素所对应的高度。此时需要计算以栈顶元素为高度的矩形的面积。
else {
//首先,将栈顶元素出栈,并保存在变量 tmp 中。
int tmp=StackTop(stk);
Pop(stk);
//计算矩形的面积,即高度乘以宽度,保存在变量 a 中。
//怎么计算矩形的宽度呢?
//如果栈为空,则宽度为当前索引 i
//【因为如果栈为空,说明出栈的元素为第一个元素,那么宽度刚好就是索引1,
//如果不是,也就是说右侧的直方图都出栈,右侧的直方图高度递减,宽度也为索引】
//否则宽度为当前索引 i 减去栈顶元素对应的索引再减去 1。
//【简单说如果不为空,此时栈中的直方图是单调递增的,但考虑那些弹出的直方图都比此时直方图小,所以就为i-StackTop(stk)-1】
int a=h[tmp]*(StackEmpty(stk)?i:i-StackTop(stk)-1);
//如果当前矩形面积 a 大于最大面积 max,则更新 max 的值。
if(max<a)
max=a;
}
}
//此时栈中剩余直方图是单调递增的,重新遍历
//保证对每个高度为h[i]的直条i,计算包含该直条的最大矩形a
while(!StackEmpty(stk)) {
//下面操作和上面一样
int tmp=StackTop(stk);
Pop(stk);
int a=h[tmp]*(StackEmpty(stk)?i:i-StackTop(stk)-1);
if(max<a)
max=a;
}
//返回最大值
return max;
}