A.World Fragments I
将两个二进制数先转换成十进制数,因为只要二进制中有1,就加或减1(加减0是没有用的),所以求两个二进制的差的绝对值(这是在有1的情况下,其实只要不等于0就有1,数是非负整数)
所以需要特判,如果第一个二进制数为0,第二个二进制数不为0,那么就不能转化,输出-1
AC代码:
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<vector>
#include<queue>
#define endl '\n'
#define int long long
using namespace std;
typedef pair<int,int>PII;
typedef long long ll;
void solve()
{
string x,y;
cin>>x>>y;
ll nx=x.size();
ll ny=y.size();
ll xx=0;
ll yy=0;
ll cnt1=0;
ll cnt2=0;
if(x=="0"&&y!="0"){
cout<<-1<<endl;
return;
}
for(int i=0;i<nx;i++){
if(x[i]=='1') {
cnt1++;
xx+=(1ll<<(nx-i-1));
}
}
for(int i=0;i<ny;i++){
if(y[i]=='1') {
cnt2++;
yy+=(1ll<<(ny-i-1));
}
}
if(xx<=yy) cout<<yy-xx<<endl;
else cout<<xx-yy<<endl;
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int t=1;
// cin>>t;
while(t--)
solve();
return 0;
}D.Ama no Jaku
首先,得将整个矩阵全部都变成0或者全部都变成1才行
证明如下:
因为题目的要求是最小的一行要大于等于最大的一列
假设最小的一行是0101,转化成十进制是5,那么其它的行都得大于等于5,所以x1和y1位置中至少有一个1,同理,x2和y2位置中至少有一个1
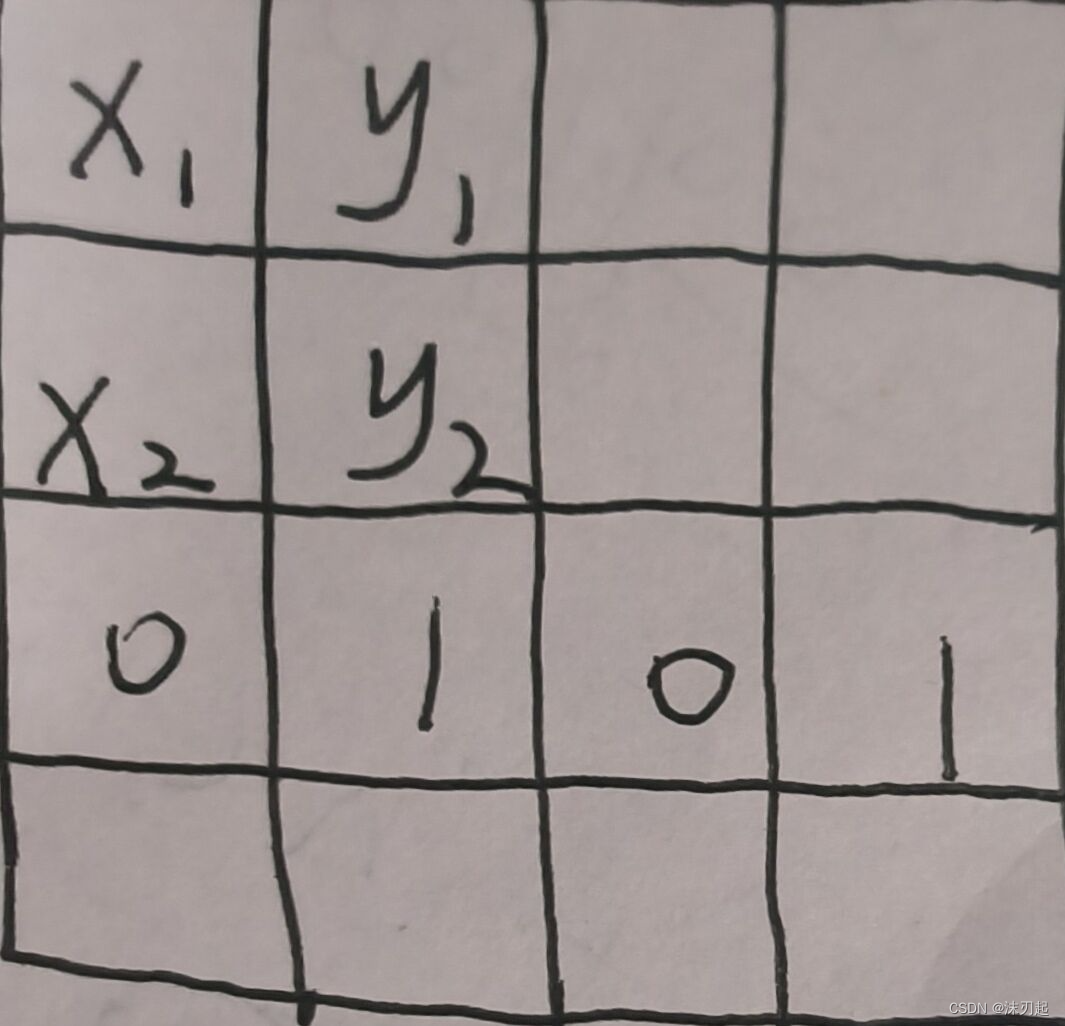
有以下几种情况:
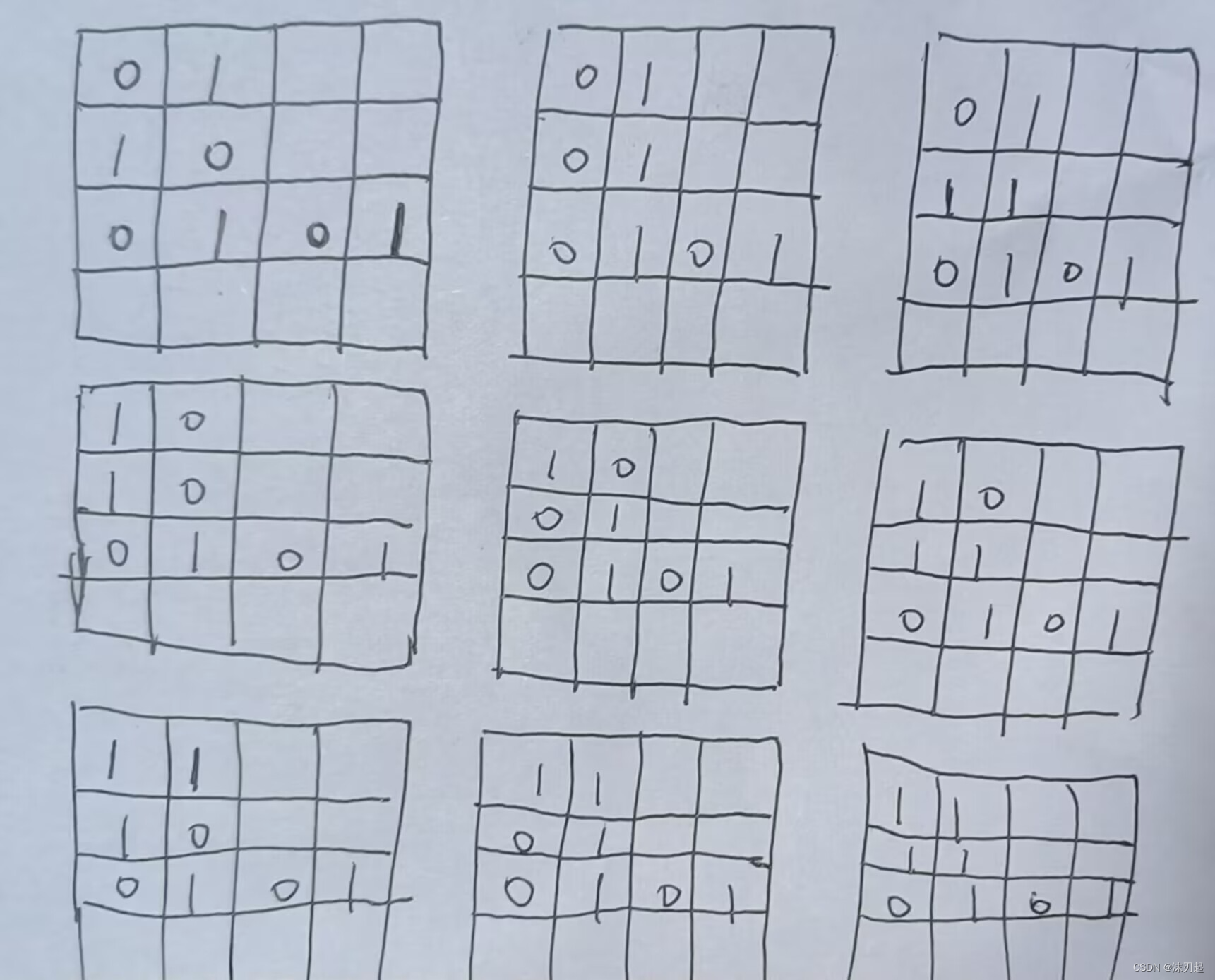
会发现,均不满足最小的行大于等于最大的列,所以只有一种情况能满足,就是将所有都变成1或者将所有都变成0
我们首先输入第一行字符串a,然后依次输入接下来的字符串b,如果字符串b要么和字符串a完全相同,要么完全相反,否则是不可能将全部都转化成0或全部都转化成1的
cnt1记录有几个字符串和a完全相反,cnt2记录字符串a中有一个字符和a[0]不一样
然后先将所有行都变得一样,操作次数为cnt1或者n-cnt1,取小的那个就行
然后将所有列都变得一样,操作次数为cnt2或者n-cnt2,取小的那个就行
最后将两者加起来
AC代码:
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<vector>
#include<queue>
#define endl '\n'
#define int long long
using namespace std;
//typedef pair<int,int>PII;
//typedef long long ll;
void solve()
{
int n;
cin>>n;
string a,b;
cin>>a;
int cnt1=0;
int cnt2=0;
for(int i=2;i<=n;i++){
cin>>b;
if(a[0]==b[0]){
for(int j=1;j<n;j++){
if(a[j]!=b[j]){
cout<<-1<<endl;
return;
}
}
}
else{
cnt1++;
for(int j=1;j<n;j++){
if(a[j]==b[j]){
cout<<-1<<endl;
return;
}
}
}
}
for(int i=1;i<n;i++){
if(a[0]!=a[i]) cnt2++;
}
cout<<min(cnt1,n-cnt1)+min(cnt2,n-cnt2)<<endl;
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int t=1;
// cin>>t;
while(t--)
solve();
return 0;
}H.Until the Blue Moon Rises
每次都选择两个数,一个加1,一个减1,需要将所有数都变成质数,因为一个数加1一个数减1,所以操作完之后所有数的和不变,所以该题就转化成了先求出n个数的和x,问x能否分解成n个质数
哥德巴赫猜想:任意一个大于2的偶数都可以分成两个质数之和
假如是n个数的和为x
当n大于等于3时(为什么要大于等于3呢?当n为偶数时,先分成一个2,再将剩下的偶数分成2个质数.当n为奇数时,先分成一个3,再将剩下的偶数分成两个质数)
对于一个大于等于2*n的偶数x,可以先将其分解成n-2个2,然后剩下的偶数大于等于4(满足大于2),所以根据哥德巴赫猜想,一定可以将剩余的偶数分解成两个质数
对于一个大于等于2*n的奇数,可以先将其分解成n-3个2,以及1个3,然后剩下一个大于等于4的偶数,同上,可以分解成两个质数
因此还需要特判n等于1以及n等于2的情况
当n等于1时,只需要判断是否是质数就行了
当n等于2时,设两数之和为x,当x为偶数并且x大于等于2*n即4时,可以分解成两个质数之和,当x为奇数时,由于质数中除了2其它全部都是奇数,也就是说只有其中一个质数是2,两个质数之和才有可能是奇数,所以只需要判断x-2是否是质数就行
AC代码:
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<vector>
#include<queue>
#define endl '\n'
#define int long long
using namespace std;
const int N=1010;
const string yes= "Yes";
const string no = "No";
int a[N];
int n;
bool check(int x){
if(x<2) return false;
for(int i=2;i<=x/i;i++){
if(x%i==0) return false;
}
return true;
}
//typedef pair<int,int>PII;
//typedef long long ll;
string solve()
{
cin>>n;
int sum=0;
for(int i=1;i<=n;i++) {
cin>>a[i];
sum+=a[i];
}
if(n==1){
if(check(sum)) return yes;
return no;
}
if(n==2){
if(sum<n*2) return no;
if(sum%2==0) return yes;
if(check(sum-2)) return yes;
return no;
}
if(sum<2*n) return no;
return yes;
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int t=1;
// cin>>t;
while(t--)
cout<<solve()<<endl;
return 0;
}J.Fine Logic
拓扑排序
赢的人排在前面,然后要求输出最小数量的排行榜,对于任意的i,j,他们的输赢关系能在排行榜中找到
如果没有环的话,就只需要一个排行榜,直接输出拓扑排序即可
如果有环的话,一个排行榜是不够的,还需要一个排行榜,即总共需要两个排行榜,第一个排行榜从1输出到n,第二个排行榜从n输出到1即可,这样就可以满足所有的输赢关系都能在排行榜中找到,因为这样的两个排行榜对于任意的i,j,既有i赢j,也有j赢i
AC代码:
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<vector>
#include<queue>
#define endl '\n'
#define int long long
using namespace std;
int n,m;
const int N=1e6+10;
int d[N];
vector<vector<int>>e(N);
//typedef pair<int,int>PII;
//typedef long long ll;
void solve()
{
cin>>n>>m;
for(int i=0;i<m;i++){
int u,v;
cin>>u>>v;
e[u].push_back(v);
d[v]++;//入度加1
}
queue<int>q;
for(int i=1;i<=n;i++){
if(!d[i]) q.push(i);
}
vector<int>ans;
while(q.size()){
int t=q.front();
q.pop();
ans.push_back(t);
for(auto v:e[t]){
d[v]--;
if(!d[v]) q.push(v);
}
}
//如果答案数量小于n,说明里面有环,有环的话就有点入度不是0,那么就不会放入答案,所以答案数量小于n
if(ans.size()<n){
cout<<2<<endl;
for(int i=1;i<=n;i++) cout<<i<<" ";
cout<<endl;
for(int i=n;i>=1;i--) cout<<i<<" ";
cout<<endl;
}
else{
cout<<1<<endl;
for(auto v:ans) cout<<v<<" ";
cout<<endl;
}
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int t=1;
// cin>>t;
while(t--)
solve();
return 0;
}E.koraidon and DFS Shortest Path
只要dfs到的点算出的距离不是最短距离,那么dfs算法就错误
可以转化成用dfs搜一遍,如果从不同的路搜到某一点,它们的距离是不一样的,那么说明算法错误
vis用于标记该点是都被搜过,保证一条路上的点只会搜一遍

1==>2==>3,然后1已经被标记过了,所以不会再搜到1
然后每次dfs完之后都要恢复现场,避免以下这种情况
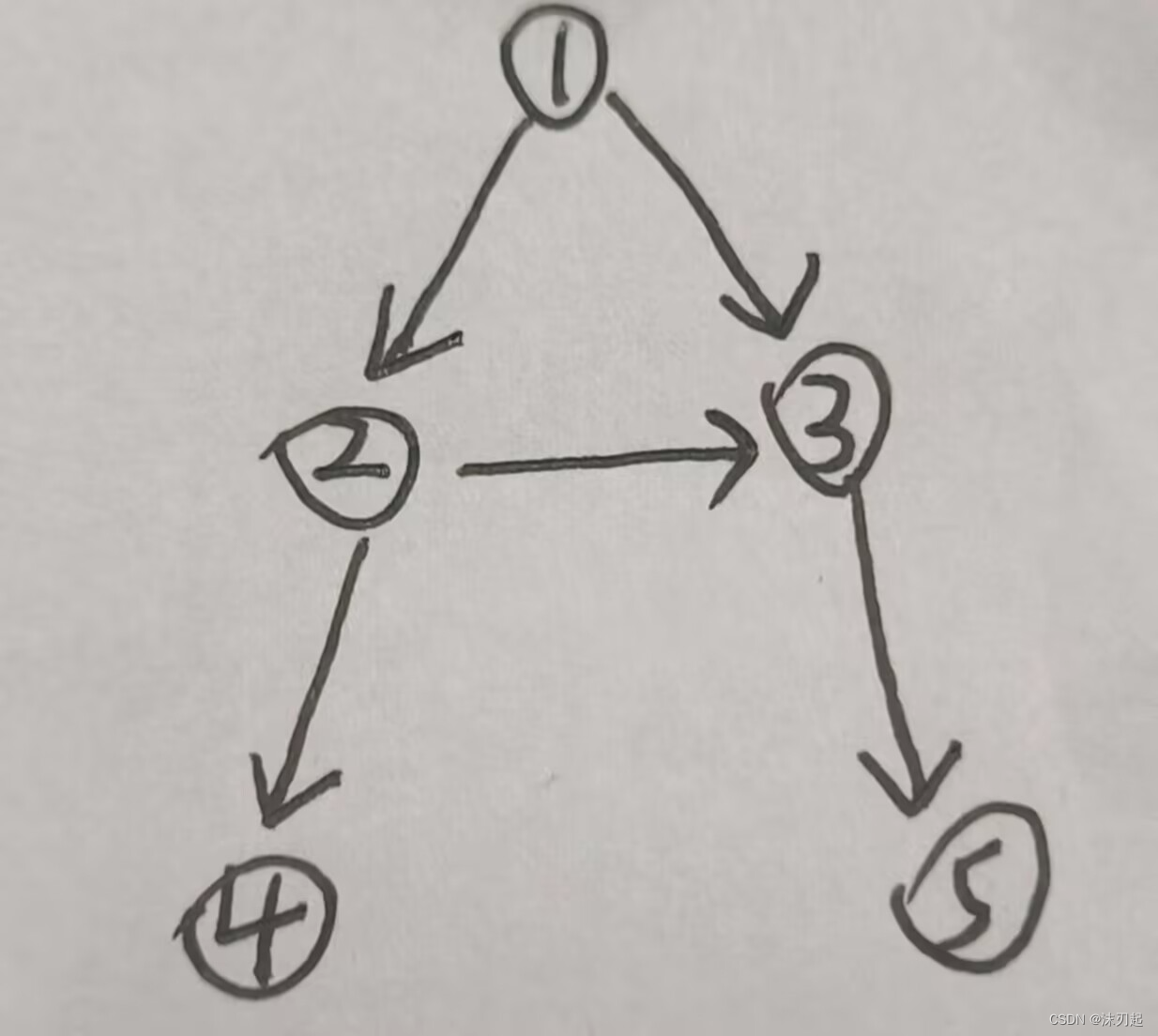
比如说我们一开始搜1==>2==>3==>5,然后如果不将3和5恢复现场的,就不能搜1==>3==>5这条路了
AC代码:
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<vector>
#include<queue>
#define endl '\n'
#define int long long
using namespace std;
//typedef pair<int,int>PII;
typedef long long ll;
const int N=1e6+10;
int a[N];
bool flag;
int n,m;
int vis[N],dist[N];
vector<vector<int>>e(N);
void dfs(int k)
{
if(!flag) return;
vis[k]=1;
for(auto kk:e[k]){
if(vis[kk]) continue;
if(!dist[kk]) dist[kk]=dist[k]+1;
else if(dist[kk]!=dist[k]+1) flag=false;
dfs(kk);
}
vis[k]=0;
}
void solve()
{
cin>>n>>m;
for(int i=1;i<=n;i++){
e[i].clear();
vis[i]=dist[i]=0;
}
for(int i=0;i<m;i++){
int u,v;
cin>>u>>v;
e[u].push_back(v);
}
flag=true;
dfs(1);
if(flag) cout<<"Yes"<<endl;
else cout<<"No"<<endl;
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int t=1;
cin>>t;
while(t--)
solve();
return 0;
}





![[Python] flask运行+wsgi切换生产环境+supervisor配置指南](https://img-blog.csdnimg.cn/0df4f0ff878c4a2b83ede2637f6cf659.png)


![ant design vue a-table表格中插入操作按钮(以switch开关 [a-switch]为例)](https://img-blog.csdnimg.cn/ac416a058ed94c1eb750ee89d0b1927d.png)