异常检测
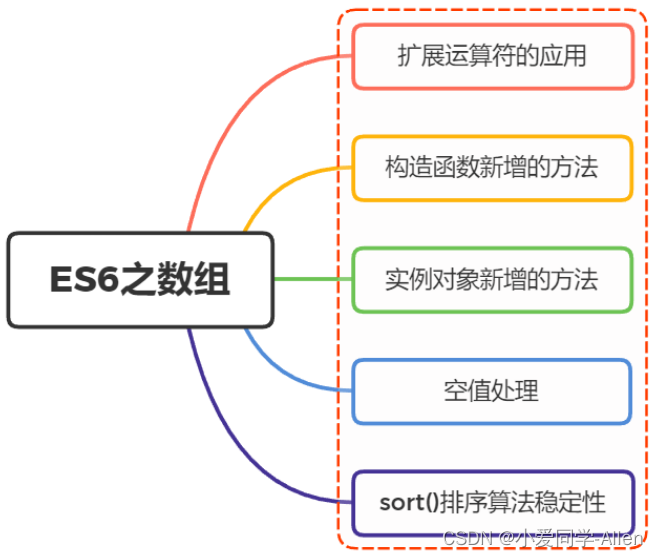
假设你是一名飞机涡扇引擎工程师,你在每个引擎出厂之前都需要检测两个指标——启动震动幅度和温度,查看其是否正常。在此之前你已经积累了相当多合格的发动机的出厂检测数据,如下图所示

我们把上述的正常启动的数据集总结为
D
a
t
a
S
e
t
:
x
(
1
)
,
x
(
2
)
,
.
.
.
,
x
(
m
)
DataSet:{x^{(1)},x^{(2)},...,x^{(m)}}
DataSet:x(1),x(2),...,x(m)
如果一个新的例子
x
t
e
s
t
x_{test}
xtest离点集很远,那可能这个样例是异常的
那么如何衡量“很远”呢?一般我们会有一个函数p(x)负责计算,并且有一个阈值 ϵ \epsilon ϵ,当 p ( x t e s t ) < ϵ p(x_{test})<\epsilon p(xtest)<ϵ的时候,我们认为该样例异常;而当 p ( x t e s t ) ≥ ϵ p(x_{test})\geq\epsilon p(xtest)≥ϵ的时候,我们认为其是正常的
异常检测的一般应用方面有欺诈检测,比如说检测一个用户的行为(登录频率,打字频率,发帖频率),来判断他是否是一个机器人。另外还可以用于计算机集群管理,通过采集各个计算机的运行数据,来找到异常的计算机,或者发掘未被充分利用的算力。
1.正态分布(高斯分布)
我们一般使用正态分布来实现异常检测,高斯分布一般用
x
∼
N
(
μ
,
σ
2
)
x\sim N(\mu,\sigma^2)
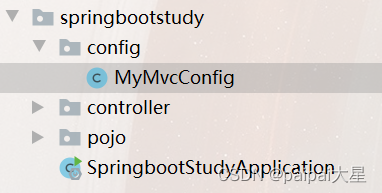
x∼N(μ,σ2)来表示,高斯分布的图像一般如下图所示,线段上的某个点
(
x
,
y
)
(x,y)
(x,y)表示的是取值为x的概率为y,其中
μ
\mu
μ是图像对称中心,而
σ
\sigma
σ被称为标准差,负责控制高斯分布的宽度,
σ
\sigma
σ越大,曲线越平滑,
σ
2
\sigma^2
σ2也称为方差
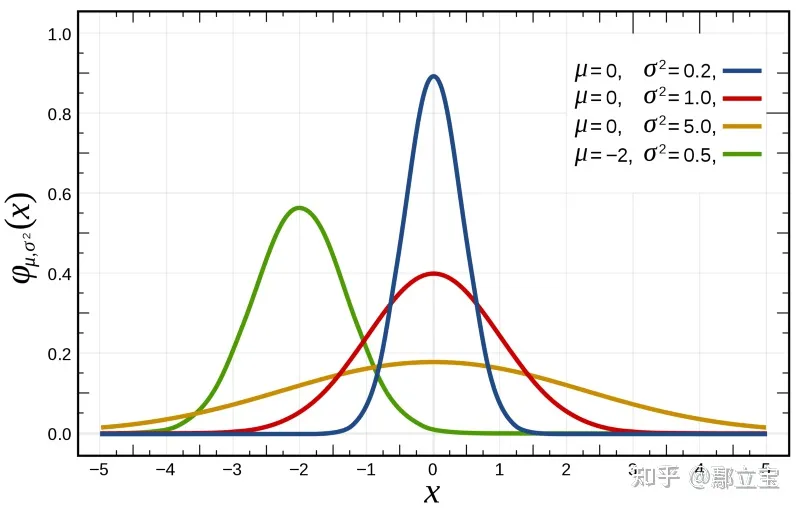
高斯概率密度公式如下:
p
(
x
,
μ
,
σ
2
)
=
1
2
π
σ
e
x
p
(
−
(
x
,
u
)
2
2
σ
2
)
p(x,\mu,\sigma ^2)=\frac{1}{\sqrt[]{2\pi }\sigma }exp\left ( -\frac{(x,u)^2}{2\sigma^2} \right )
p(x,μ,σ2)=2πσ1exp(−2σ2(x,u)2)
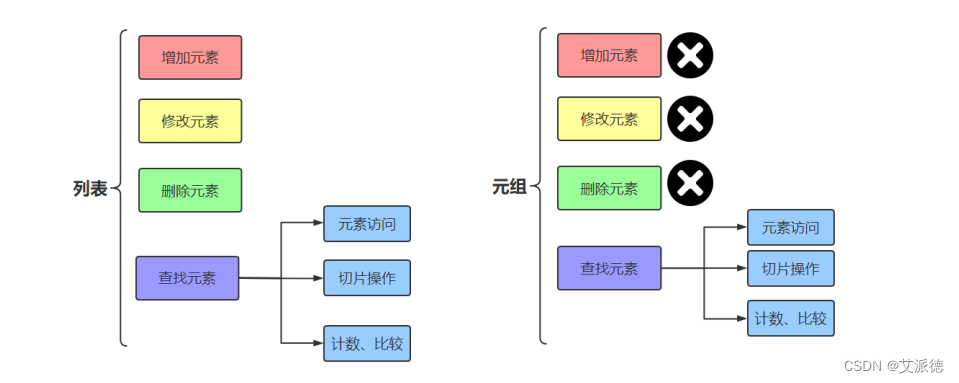
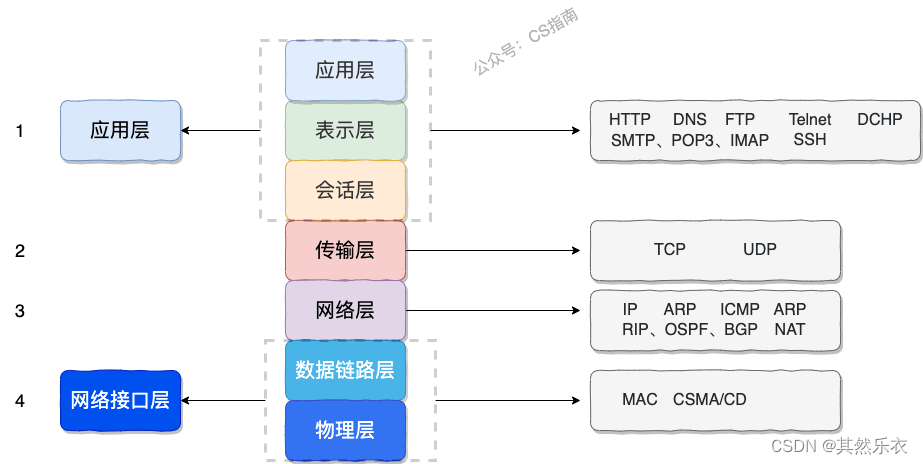
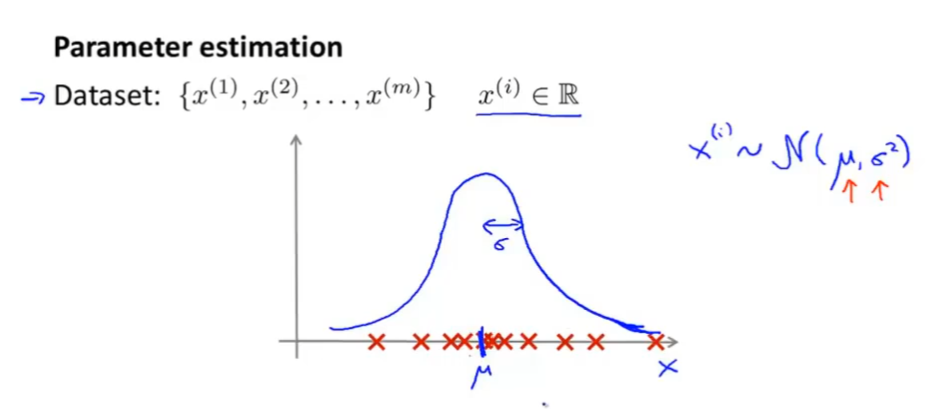
认识了高斯分布后,假设我们有一个数据集x,它的每个样例中仅有一个特征,那么这些数据集可以直接表示在x轴上,如下图:
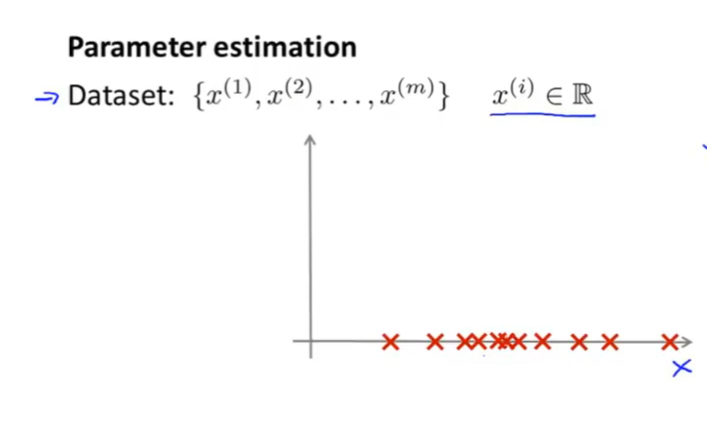
那么我们需要做的事情是根据数据集在图上的离散分布,估计出 μ \mu μ和 σ 2 \sigma^2 σ2值,找到符合该数据集的高斯分布
对于
μ
\mu
μ的取值,实际上就是找数据中心,一般是找所有点在x轴上的均值,计算方式就是
μ
=
1
m
∑
i
=
1
m
x
(
i
)
\mu=\frac{1}{m}\sum_{i=1}^{m}x^{(i)}
μ=m1i=1∑mx(i)
而对于
σ
2
\sigma^2
σ2,其实是一个计算点集的方差的过程,也就是整体离中心点的偏移大小,计算方式是
μ
=
1
m
∑
i
=
1
m
(
μ
−
x
(
i
)
)
2
\mu=\frac{1}{m}\sum_{i=1}^{m}(\mu -x^{(i)})^2
μ=m1i=1∑m(μ−x(i))2
2.使用高斯分布构建异常检测算法
上述我们说了如果一个实例中只有一个特征,如何建立其高斯分布,那么如果一个实例有n个特征呢?实际上很简单,对于一个有m个实例,每个实例有n个特征的数据集,我们需要对每一个特征都建立一个高斯分布,而每一个高斯分布都有m个数据,共计n个高斯分布。
步骤一:对于一个实例 x x x,选择出若干特征 x i x_i xi,这些特征应该可以反映出实例x是否异常
步骤二:该步骤上文已经提到过,就是对于所有实例的第j个特征 x j x_j xj,都有一个高斯函数 x j N ( μ j , σ j 2 ) x_j~N(\mu_j,\sigma^2_j) xj N(μj,σj2)用于计算该特征下的高斯分布, μ j , σ j 2 \mu_j,\sigma^2_j μj,σj2的计算方式参考上一节
步骤三
对于一个训练集
D
a
t
a
S
e
t
:
x
(
1
)
,
x
(
2
)
,
.
.
.
,
x
(
m
)
DataSet:{x^{(1)},x^{(2)},...,x^{(m)}}
DataSet:x(1),x(2),...,x(m),每个样本x都拥有若干个特征,对于某个样本
x
x
x,对它的
p
(
x
)
p(x)
p(x)的计算方法是
p
(
x
)
=
∏
n
j
=
1
p
(
x
j
,
μ
j
,
σ
j
2
)
=
p
(
x
1
,
μ
1
,
σ
1
2
)
p
(
x
2
,
μ
2
,
σ
2
2
)
p
(
x
3
,
μ
3
,
σ
3
2
)
.
.
.
p
(
x
n
,
μ
n
,
σ
n
2
)
p(x)=\prod_{n}^{j=1}p(x_j,\mu_j,\sigma ^2_j) =p(x_1,\mu_1,\sigma ^2_1)p(x_2,\mu_2,\sigma ^2_2)p(x_3,\mu_3,\sigma ^2_3)...p(x_n,\mu_n,\sigma ^2_n)
p(x)=n∏j=1p(xj,μj,σj2)=p(x1,μ1,σ12)p(x2,μ2,σ22)p(x3,μ3,σ32)...p(xn,μn,σn2)
最后我们规定一个阈值 ϵ \epsilon ϵ,当 p ( x ) < ϵ p(x)<\epsilon p(x)<ϵ的时候,我们认为该实例x异常
3.开发和评估异常检测系统
和其他算法一样,我们将训练模型的数据分为训练集,交叉验证集和测试集。假设我们有10000个正常的数据,20个异常的数据,那么我们可以这样子分配:
- 训练集含有6000个正常数据
- 交叉验证集含有2000个正常数据,10个异常数据
- 测试集含有2000个正常数据,10个异常数据
接下来就是使用数据训练 p ( x ) p(x) p(x)函数,并且当 p ( x ) < ϵ p(x)<\epsilon p(x)<ϵ的时候,我们认为该实例x异常,训练的过程在上一小节已经说明了
4.异常检测和无监督学习的区别
对于异常检测,他的应用场景更多的是在异常点相对少的情况下,比如10000台发动机中只有20台需要返修。而无监督学习更多的是正样本和负样本的数据相当。这也是为什么异常检测广泛应用在制造业和数据监控行业,因为其出现异常的概率相对比较低;而在垃圾邮件识别方面,大量的垃圾邮件样例为无监督学习提供了丰富的负样本,因此使用无监督学习更好
另外的一方面是,无监督学习擅长划分若干个点集,比如将发动机划分为正常、喘振、压气机失速等若干种情况,但是如果第二天出现了叶片共振的问题,无监督学习就束手无策了,因为它没见过这种情况。
而异常检测就是简单地粗暴地将正常工作的情况划分出来,只要超出了正常的限界都被认为是异常,因此当叶片共振这种之前未出现的故障出现的时候,异常检测算法会直接认为它是异常,而不会细究其异常的原因,但是这也反而使得它具有了识别一些之前未出现的异常的能力