本文重点

在前面的课程中，我们学习了单变量线性回归模型以及多变量的线性回归模型，无论是单变量线性回归还是多变量线性回归，这二者都是一样的，都是线性的。本文我们将学习一下线性回归模型和非线性回归之间的区别和联系。

关于模型的基本区别

线性回归：线性回归就是每个变量的指数都是1，它的形态是直线形态或者是超平面形态。线性回归模型假设因变量与自变量之间的关系是线性的。线性回归模型的形式为：y = β0 + β1x1 + β2x2 + ... + βnxn，其中y表示因变量，x1, x2, ..., xn表示自变量，β0, β1, β2, ..., βn表示模型的系数。

 

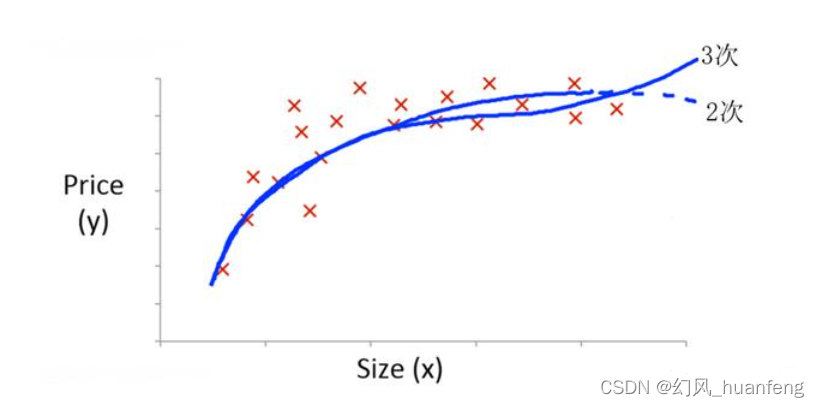
非线性回归：非线性回归模型的形式可以是任意的非线性函数，例如多项式函数（至少有一个变量的指数不是1）、指数函数、对数函数等。它的形态是曲线形态。非线性回归模型假设因变量与自变量之间的关系是非线性的。

拟合能力

线性回归模型适用于因变量与自变量之间的关系是线性的情况，对于非线性关系的数据拟合效果较差。线性回归模型的拟合能力受到线性假设的限制，无法很好地拟合复杂的非线性关系。

非线性回归模型适用于因变量与自变量之间的关系是非线性的情况，可以更好地拟合非线性关系的数据。非线性回归模型的拟合能力较强，能够更准确地描述因变量与自变量之间的复杂关系。

参数学习

线性回归模型的参数估计可以通过最小二乘法来进行，即通过最小化