前言

本篇是动态规划系列的入门基础题,以"第 n 个泰波那契数"和 "三步问题"为例子.

一、第 n 个泰波那契数

题目来源于:力扣
题目链接:传送门

题目描述:

泰波那契序列 Tn 定义如下：
T0 = 0, T1 = 1, T2 = 1, 且在 n >= 0 的条件下 Tn+3 = Tn + Tn+1 + Tn+2给你整数 n，请返回第 n 个泰波那契数 Tn 的值。

示例 1:

输入：n = 4
输出：4
解释：
T_3 = 0 + 1 + 1 = 2
T_4 = 1 + 1 + 2 = 4

示例2:

输入：n = 25
输出：1389537

算法讲解:

创建dp表.
确定状态表示:用dp[n]表示第 n 个泰波那契数 Tn 的值.
我们要返回Tn的值,也就是第n个泰波那契数,由于T0的存在(即有第0个泰波那契数),所以我们创建dp表的时候,需要创建n+1个大小的数组,即dp[n+1].
·需要设置的文字
初始化.
前面三个泰波那契数的值题目都已经给出,dp[0]=0,dp[1]=1,dp[2]=1;
填写dp表.
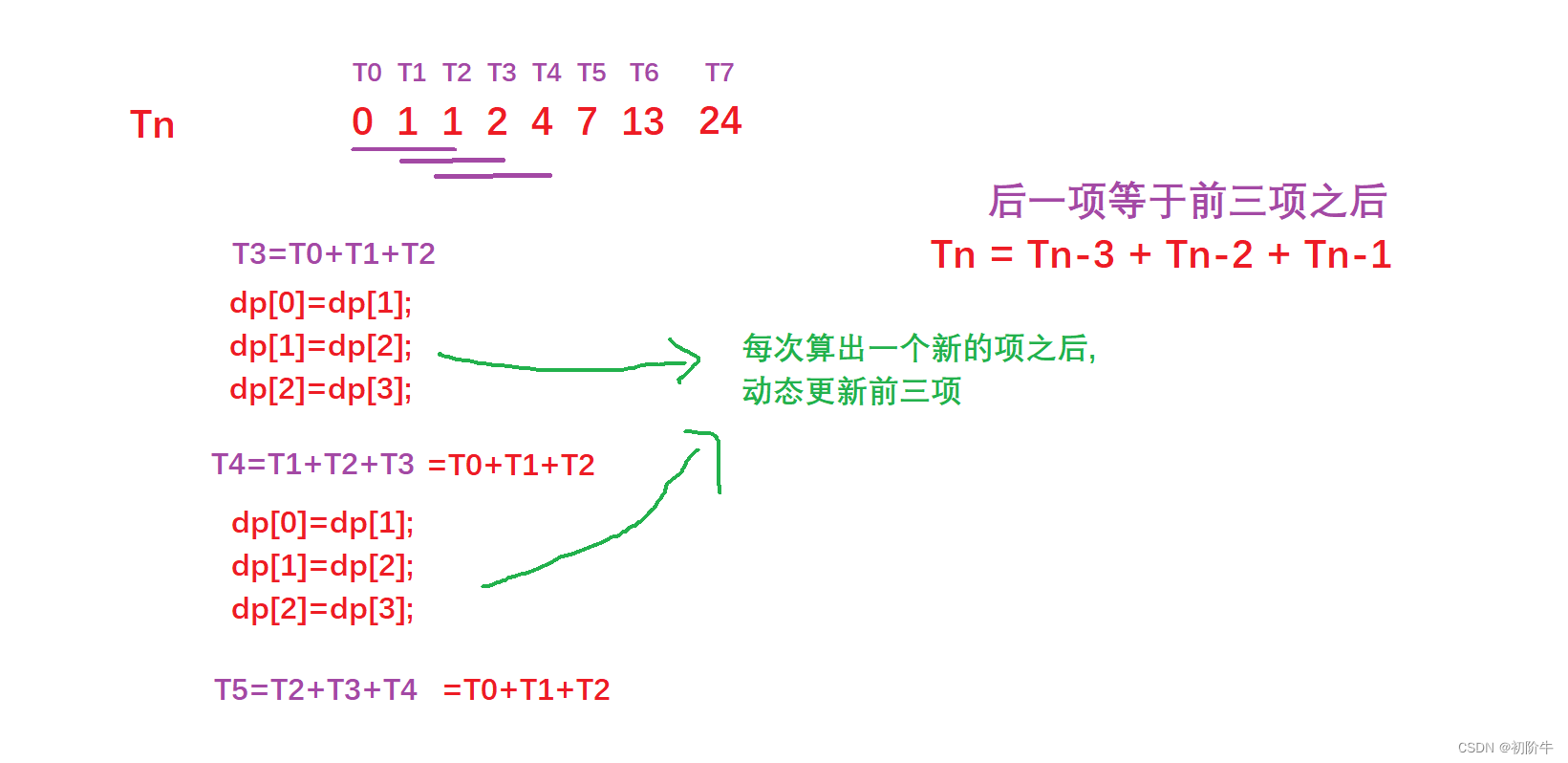
根据题目介绍,我们不难得出状态转移方程是:Tn+3 = Tn + Tn+1 + Tn+2
即:Tn = Tn-3 + Tn-2 + Tn-1

在这里插入图片描述

本题中是直接给出了状态转移方程,大多数动态规划的题目是需要我们自己推导的.

确认返回值.
题目要求返回第 n 个泰波那契数 Tn 的值,那dp[n]不就是我们需要返回的吗?
细节处理:
由于0<n<=2时,无法进行完整的初始化操作,我们可以提前进行判定直接返回.

代码实现:

class Solution {
public:
    int tribonacci(int n) {
        //防止因为n过小导致的初始化问题
        if(n==0) return 0;
        if(n==1||n==2)return 1;

        //1.创建dp表
        int dp[n+1];
        //2.初始化
        dp[0]=0,dp[1]=1,dp[2]=1;
        //3.填表
        for(int i=3;i<=n;i++)
        {
            dp[i]=dp[i-3]+dp[i-2]+dp[i-1];
        }
        //4.确认返回值
        return dp[n];
    }
};

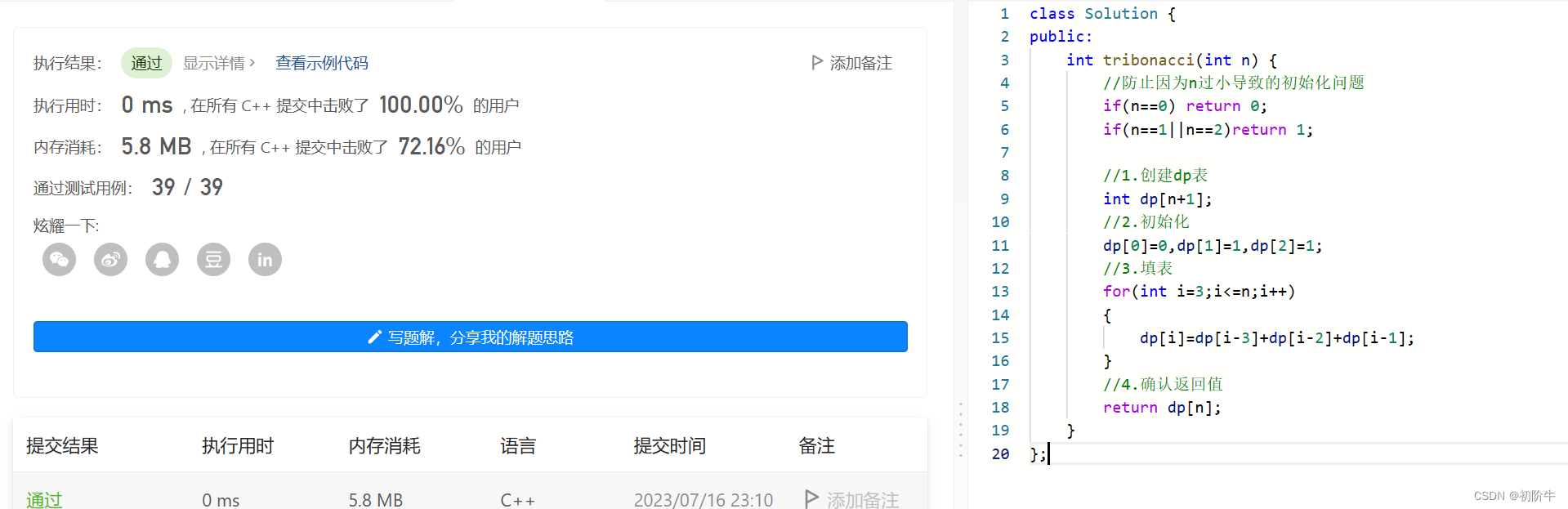
空间优化:

在上面的算法中,我们创建了n+1个大小的数组空间,所以空间复杂度是O(n),我们可以采用滚动数组的方法,将时间复杂度降到O(1).

其实我们可以不用创建n+1个大小的数组空间,因为只需要知道第n项的前三个,就可以推导出第四项,所以我们可以创建只有四个大小的数组空间.

在这里插入图片描述

class Solution {
public:
    int tribonacci(int n) {
        //防止因为n过小导致的初始化问题
        if(n==0) return 0;
        if(n==1||n==2)return 1;

        //1.创建dp表
        int dp[4];
        //2.初始化
        dp[0]=0,dp[1]=1,dp[2]=1;
        //3.填表
        for(int i=3;i<=n;i++)
        {
            dp[3]=dp[2]+dp[1]+dp[0];
            //动态更新数组(滚动数组)
            dp[0]=dp[1];
            dp[1]=dp[2];
            dp[2]=dp[3];
        }
        //4.确认返回值
        return dp[3];
    }
};

在这里插入图片描述

二、三步问题

题目来源于:力扣
题目链接:传送门

题目描述:

三步问题。有个小孩正在上楼梯，楼梯有n阶台阶，小孩一次可以上1阶、2阶或3阶。实现一种方法，计算小孩有多少种上楼梯的方式。结果可能很大，你需要对结果模1000000007。

示例1:

输入：n = 3
输出：4
说明: 有四种走法

示例2:

输入：n = 5
输出：13

算法讲解:

创建dp表:
确定状态表示:dp[n]代表有n阶楼梯时,小孩可以选择上楼的方式.
我们要j计算的是当有n阶台阶时,小孩有多少种上楼梯的方式.
并且此题规定:0个台阶时,有一种上楼方式.
所以我们创建dp表的时候,需要创建n+1个大小的数组,即dp[n+1].
初始化:
上楼梯的方法:dp[0]=1,dp[1]=1,dp[2]=2;
填写dp表.
先看懂题目意思,此题需要自行推导状态转移方程.
分析: dp[0]=1,dp[1]=1.

在这里插入图片描述
4. 确认返回值:
dp[n]代表有n阶楼梯时,我们可以选择的上楼方式.所以返回dp[n]即可.

5.细节处理:
(1)由于0<n<=2时,无法进行完整的初始化操作,我们可以提前进行判定直接返回.
(2)由于这里数据比较大,所以每次进行"+"运算时,需要进行对结果取模(1000000007).

代码实现:

class Solution {
public:
    int waysToStep(int n) {
        const int MOD =1000000007;
        
        //防止因为n过小导致的初始化问题
        if(n==0||n==1)return 1;
        if(n==2)return 2;
		
		//创建dp数组
        int dp[n+1];
        //初始化操作
        dp[0]=1,dp[1]=1,dp[2]=2;
        //填表
        for(int i=3;i<=n;i++)
        {
            dp[i]=((dp[i-3]+dp[i-2])%MOD+dp[i-1])%MOD;//这里一定要记得取模
        }
        //返回值
        return dp[n];
    }
};