文章目录
- 一、算法原理
- 二、算法实战
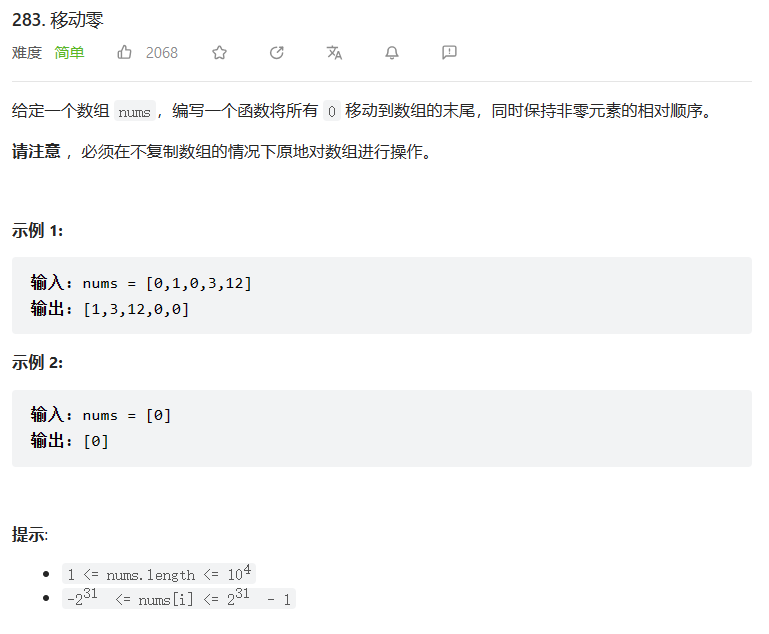
- 1. 力扣283 移动零
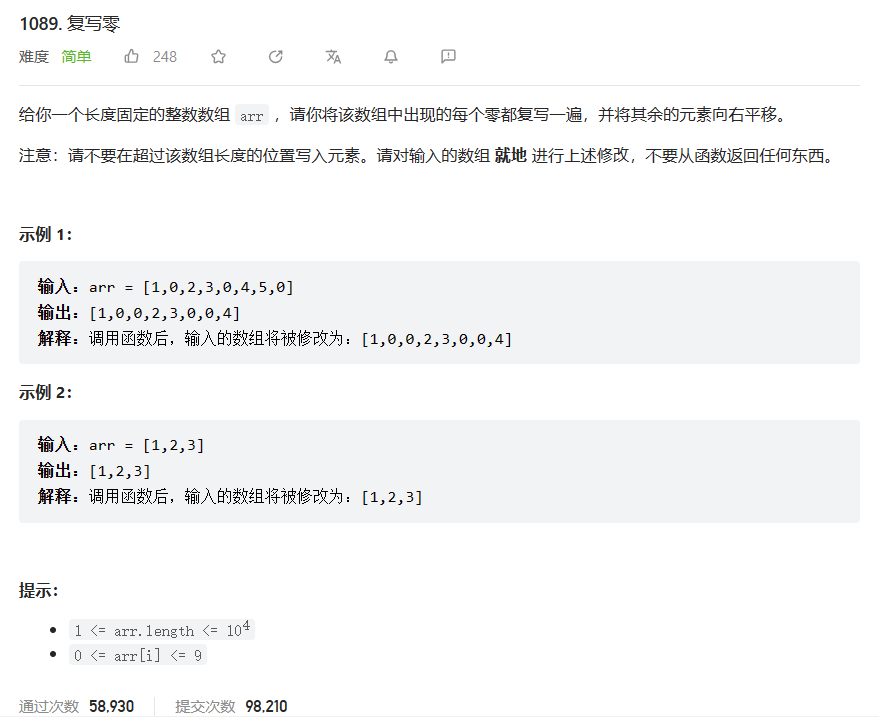
- 2. 力扣1089 复写零
- 3. 力扣15 三数之和
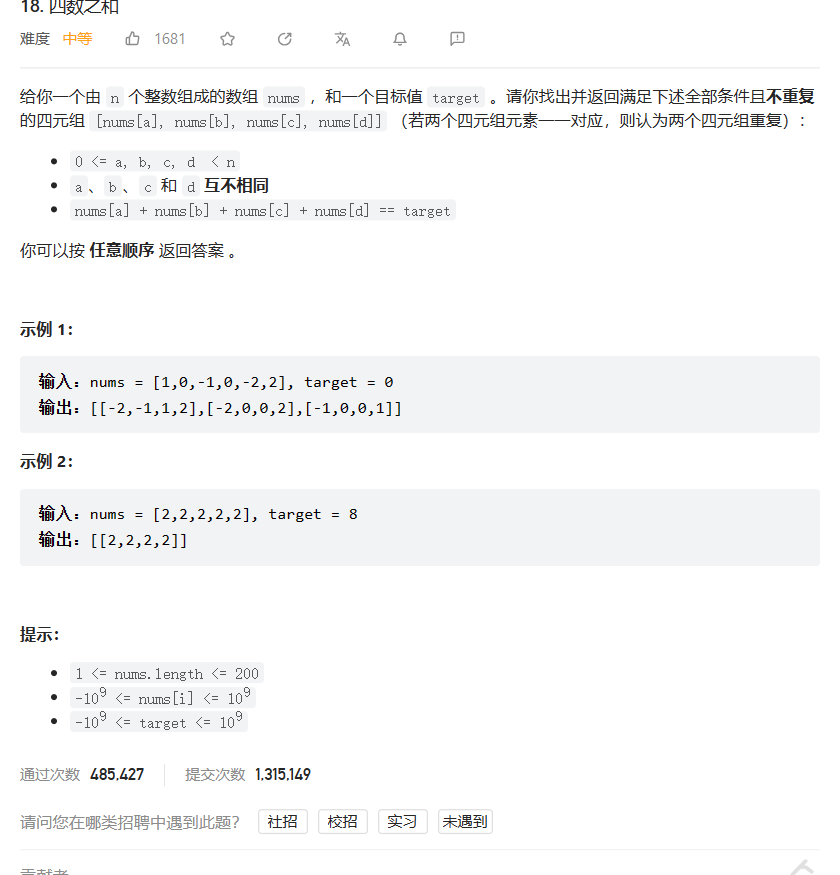
- 4. 力扣18 四数之和
- 三、总结
一、算法原理
双指针算法是指在遍历对象的过程中不是普通的使用单个指针进行访问,而是使用两个相同方向(快慢指针)或者相反方向(对撞指针)的指针进行扫描,从而达到相应的目的。常见的双指针算法有两种:
在一个序列里,用两个指针维护一段区间在两个序列里,一个指针指向一个序列,另外一个指针指向另外一个序列,来维护某种次序。
💕 算法模板
for (int i = 0, j = 0; i < n; i ++ ) // j从某一位置开始,不一定是0
{
while (j < i && check(i, j)) j ++ ;
// 具体问题的逻辑
}
常见问题分类:
(1) 对于一个序列,用两个指针维护一段区间,比如快排的划分过程
(2) 对于两个序列,维护某种次序,比如归并排序中合并两个有序序列的操作
二、算法实战
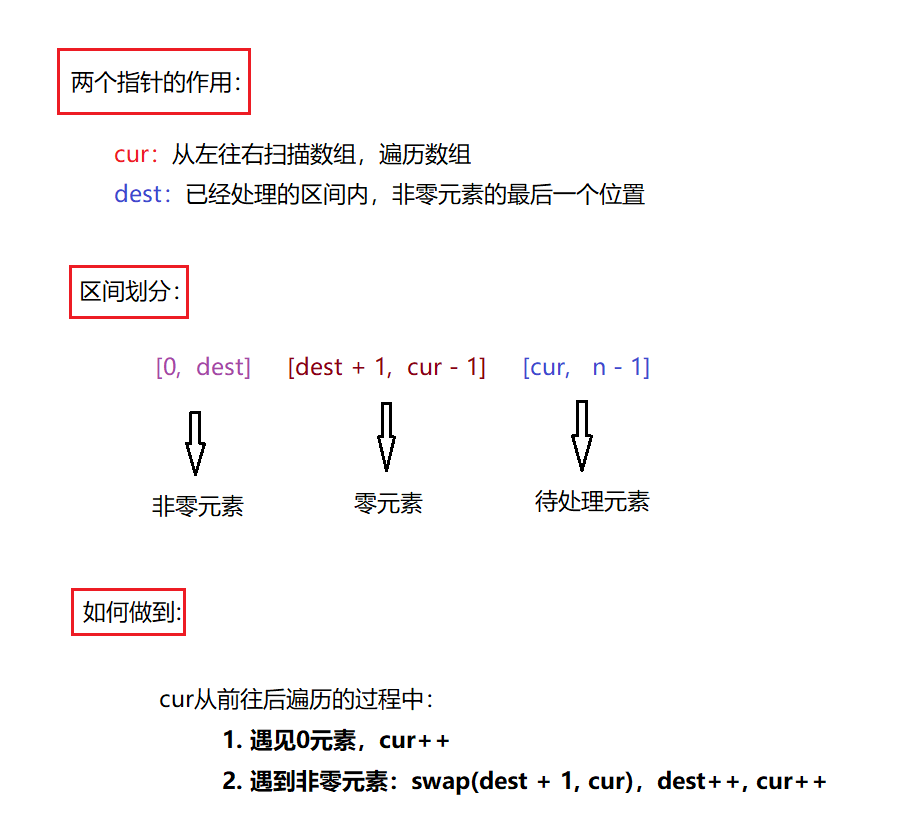
1. 力扣283 移动零
题目链接
算法原理:
代码实现:
class Solution {
public:
void moveZeroes(vector<int>& nums) {
for(int dest = -1, cur = 0; cur < nums.size(); cur++)
if(nums[cur])
swap(nums[++dest], nums[cur]);
}
};
2. 力扣1089 复写零
复写零
算法原理:

代码实现:
class Solution {
public:
void duplicateZeros(vector<int>& arr) {
//从前向后遍历,寻找cur和dest的位置
int dest = -1, cur = 0, n = arr.size();
for(cur = 0; cur < n; cur++)
{
if(arr[cur] == 0)
dest+=2;
else
dest++;
if(dest >= n - 1)
break;
}
if(dest == n)
{
arr[n - 1] = 0;
dest-=2, cur--;
}
while(cur >=0 && dest >= 0)
{
if(arr[cur] == 0)
arr[dest--] = 0;
arr[dest--] = arr[cur];
cur--;
}
}
};
3. 力扣15 三数之和
三数之和
算法原理:
本题我们采用 “排序+双指针” 的思想。先将数组排序,用一层循环来枚举第一个数,当我们确定第一个元素后,另外两个元素n2+n3之和就变成了一个定值。当n2增大时n3减小,当n2减小时n3增大。
这样我们就可以在确定第一个元素后,运用双指针来同时确定第二个和第三个元素的值。当然这里我们一定要注意去重的问题,在枚举的过程中就将去重的工作顺便做了即可。
代码实现:
class Solution {
public:
vector<vector<int>> threeSum(vector<int>& nums) {
int n = nums.size();
sort(nums.begin(), nums.end());
vector<vector<int>> ret;
if(nums[0] > 0 || nums[n - 1] < 0 || n < 3)
return ret;
if(nums[0] == 0 && nums[n - 1] == 0)
return {{0,0,0}};
//双指针算法
for(int i = 0; i < n - 2; i++)
{
//去重
if(i && nums[i] == nums[i - 1])
continue;
if(nums[i] > 0)
break;
int left = i + 1, right = n - 1;
while(left < right)
{
int sum = nums[i] + nums[left] + nums[right];
if(sum < 0)
left++;
else if(sum > 0)
right--;
else
{
ret.push_back({nums[i], nums[left], nums[right]});
left++,right--;
// 去重
while(left < right && nums[left] == nums[left - 1])
left++;
while(left < right && nums[right] == nums[right + 1])
right--;
}
}
}
return ret;
}
};
4. 力扣18 四数之和
四数之和
算法原理:
四数之和可以在三数之和的基础上做一下修改,三数之和通过双指针解法可以将时间复杂度降到O(n2),四数之和通过双指针的方法可以将时间复杂度降到 O(n3)。具体方法为:
- 外面双层循环,代表四个数中的前两个数。
- 里面为一首一尾双指针,代表四个数中的后两个数,双指针逐步往中间移动,直至相遇。
代码实现:
class Solution {
public:
vector<vector<int>> fourSum(vector<int>& nums, int target) {
int n = nums.size();
sort(nums.begin(), nums.end());
vector<vector<int>> ret;
for(int i = 0; i < n - 3; i++)
{
if(i && nums[i] == nums[i - 1])
continue;
for(int j = i + 1; j < n - 2; j++)
{
if(nums[j] == nums[j - 1] && j != i + 1)
continue;
long long sum = (long long)target - nums[i] - nums[j];
int left = j + 1, right = n - 1;
while(left < right)
{
if(nums[left] + nums[right] < sum)
left++;
else if(nums[left] + nums[right] > sum)
right--;
else
{
ret.push_back({nums[i], nums[j], nums[left], nums[right]});
left++,right--;
while(left < right && nums[left] == nums[left - 1])
left++;
while(left < right && nums[right] == nums[right + 1])
right--;
}
}
}
}
return ret;
}
};
三、总结
双指针算法的用途非常的广泛,在数组和链表的操作中是非常常见的,当我们运用双指针时,需要找到目标对象的性质——单调性,当然也必须别忘了指针i和指针j的范围更新问题。最后,多刷题、多总结才能将其运用得当哦!