A - Not OverflowA - Not Overflow

题目大意

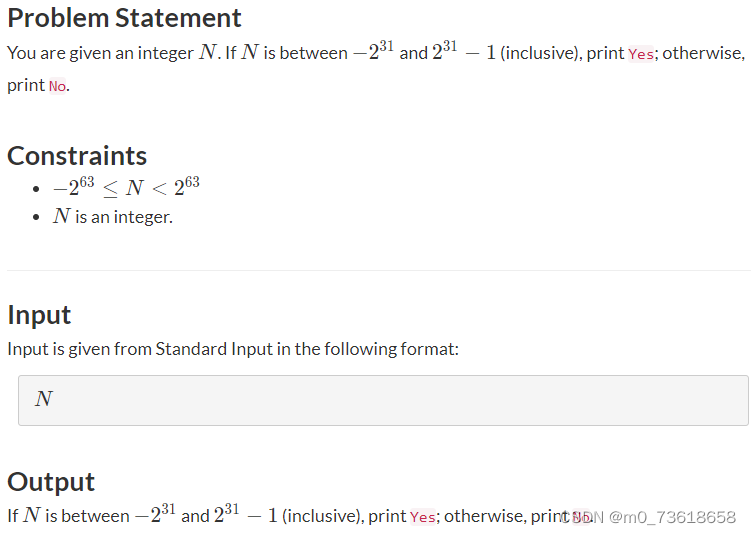
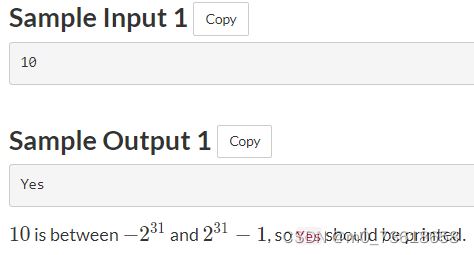
题目要求判断给定的整数N是否在范围[-2³¹, 2³¹-1]内，如果是则输出"Yes"，否则输出"No"。

思路分析

位运算：由于题目中的范围是2的幂次方，可以使用位运算来进行快速计算。

时间复杂度

O(1)

AC代码

#include<bits/stdc++.h>
using namespace std;
using ll=long long;

int main() {
  ll n;
  ll m = (ll)1 << 31; // 将1左移31位，得到2^31的值
  cin >> n;
  
  if((-m <= n) && (n < m)) 
    cout << "Yes" << endl;
  else
    cout << "No" << endl;
    
  return 0;
}

B - Matrix TranspositionB - Matrix Transposition

题目大意

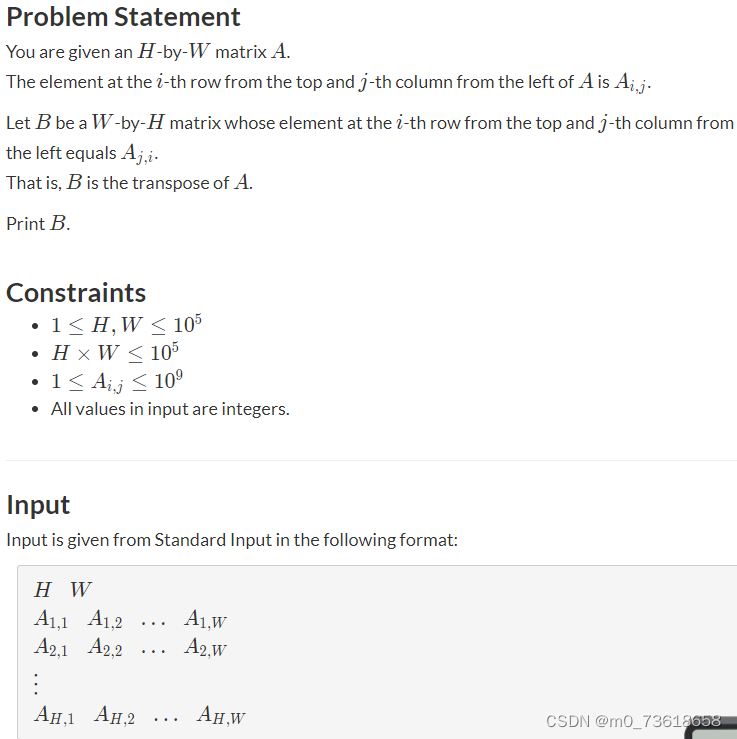
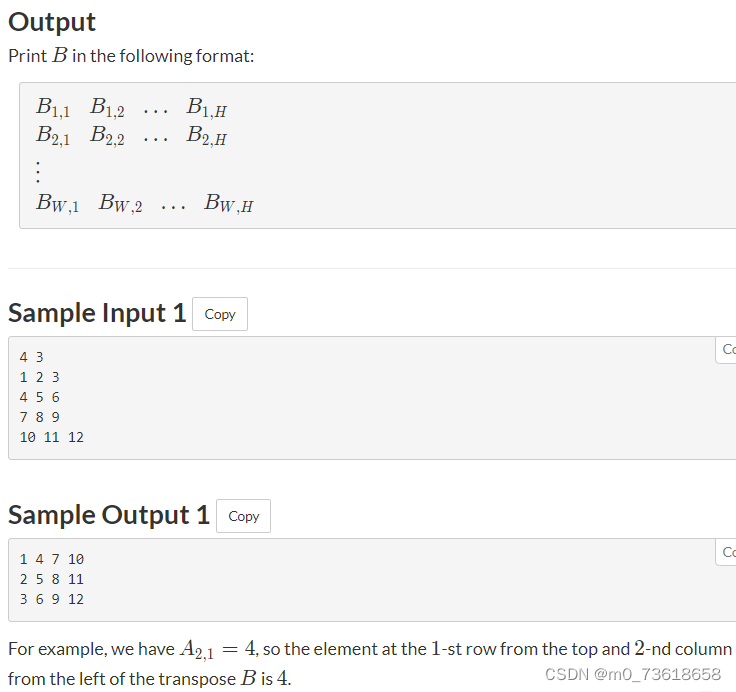
题目要求将给定的H行W列的矩阵A转置为W行H列的矩阵B，并输出B。

思路分析

根据题目要求，需要将矩阵A的行变为B的列，列变为B的行。可以使用两个二维数组A和B来存储输入和输出矩阵。首先遍历A矩阵，将元素存储到对应位置的B矩阵中。然后再遍历B矩阵，按要求输出B。

时间复杂度

O(H * W)

AC代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;

int main(){
    ll h, w;
    cin >> h >> w;
    ll a[h][w], b[w][h]; 
    for(ll i = 0; i < h; i++){
        for(ll j = 0; j < w; j++){
            cin >> a[i][j];
            b[j][i] = a[i][j]; 
        }
    }
    for(ll i = 0; i < w; i++){
        for(ll j = 0; j < h; j++){
            cout << b[i][j];
            if(j < h - 1)
                cout << " ";
            else 
                cout << endl;
        }
    }

    return 0;
}

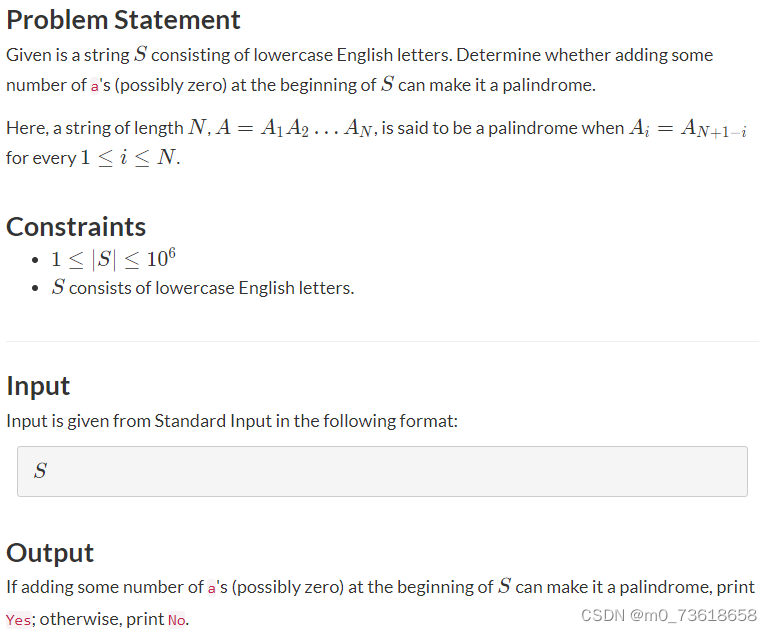
C - kasakaC - kasaka

题目大意

题目要求判断是否可以在字符串SS的开头添加一些a（可能为零），使其成为回文串。如果可以，输出"Yes"；否则输出"No"。

思路分析

如果S本身就是由’a’组成的，那么无论添加多少个a都可以构成回文串，输出"Yes"。
如果S包含除’a’以外的字符，我们需要判断是否能通过添加a的方式构成回文串。可以从S的开头开始统计连续的’a’的数量x，然后从S的末尾开始统计连续的’a’的数量y。如果x大于y，则无论如何添加a都不能构成回文串，输出"No"。否则，只需要检查SS中剩余部分（即从第x+1个字符到倒数第y个字符）是否对称，即可判断是否能构成回文串。

时间复杂度

O(∣S∣)

知识点

双指针，回文串

AC代码

#include <bits/stdc++.h>
using namespace std;

int main(void) {
	int n, x, y;
	string a;

	cin >> a;
	n = a.size();

	x = 0;
	for (int i = 0; i < n; i++) {
		if (a[i] == 'a')x++;
		else break;
	}
	y = 0;
	for (int i = n - 1; i >= 0; i--) {
		if (a[i] == 'a')y++;
		else break;
	}

	if (x == n) {
		cout << "Yes" << endl;
		return 0;
	}
	if (x > y) {
		cout << "No" << endl;
		return 0;
	}
	for (int i = x; i < (n - y); i++) {
		if (a[i] != a[x + n - y - i - 1]) {
			cout << "No" << endl;
			return 0;
		}
	}
	cout << "Yes" << endl;
	return 0;
}