(40条消息) flask 读取文件夹文件,展示在页面,可以通过勾选删除_U盘失踪了的博客-CSDN博客
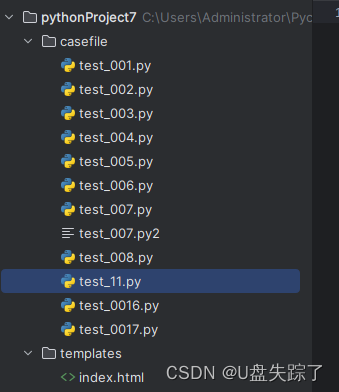
项目结构
这是一个基本的Flask应用程序,主要有两个路由,一个是index,用于显示所有存在的文件以及用于删除已选的文件;另一个是new_file,用于创建新的文件。它检查用户输入的文件名是否已经存在,如果存在,就返回一个错误消息,并在HTML中显示。
app.py
from flask import Flask, render_template, request, redirect, url_for
import os
import glob
app = Flask(__name__)
app.config['UPLOAD_FOLDER'] = os.getcwd() + '/casefile'
@app.route('/', methods=['GET', 'POST'])
def index():
if request.method == 'POST':
to_delete = request.form.getlist('checks')
for file in to_delete:
os.remove(file)
return redirect(url_for('index'))
files = glob.glob('casefile/test*.py') # adjust this to your needs
return render_template('index.html', files=files)
@app.route('/new', methods=['GET', 'POST'])
def new_file():
# 定义错误消息
error = None
# 定义开关
switch = False
if request.method == 'POST':
filename = request.form.get('filename')
files = glob.glob('casefile/test*.py')
# 遍历当前casefile文件夹的所有文件,切片处理文件
for i in files:
if str(i[9:]) == str(filename):
error = '文件名称重复,请修改'
switch = True
# 不成立时,创建文件
if switch == False:
content = request.form.get('content')
with open(os.path.join(app.config['UPLOAD_FOLDER'], filename), 'w') as f:
f.write(content)
# return redirect(url_for('index'))
# 返回页面错误消息
return render_template('new_file.html', error=error)
if __name__ == '__main__':
app.run(debug=True)templates/index.html
<!doctype html>
<html lang="en">
<head>
<title>File Deleter</title>
</head>
<body>
<h1>Select Files To Delete</h1>
<form method="POST">
{% for file in files %}
<input type="checkbox" name="checks" value="{{ file }}"> {{ file }}<br />
{% endfor %}
<input type="submit" value="Delete">
</form>
</body>
</html>
templates/new_file.html
在 <textarea> 标签中使用 rows 和 cols 属性来设定文本框的大小。rows 属性定义文本框的行数,cols 属性定义文本框的列数
resize: both; 允许用户调整文本框的宽度和高度。如果你只想允许用户调整文本框的宽度,你可以使用 resize: horizontal;,如果你只想允许用户调整文本框的高度,你可以使用 resize: vertical;。如果你不想允许用户调整文本框的大小,你可以使用 resize: none;
<!DOCTYPE html>
<html>
<head>
<title>New File</title>
</head>
<style>
textarea {
resize: both;
}
</style>
<body>
<h1>New File</h1>
<form method="POST">
<label for="filename">Filename:</label><br>
<input type="text" id="filename" name="filename"><br>
<label for="content">Content:</label><br>
<textarea id="content" name="content" rows="10" cols="50"></textarea><br>
<input type="submit" value="Save">
</form>
{% if error %}
<p><strong>Error</strong>:{{ error }}</p>
{% endif %}
</body>
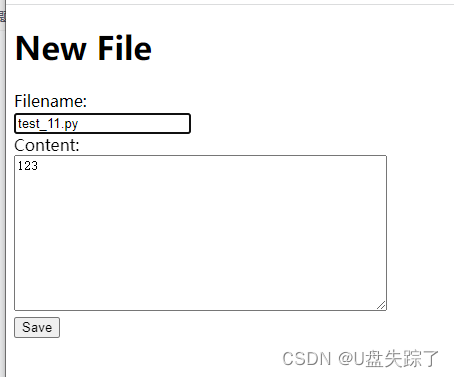
</html>示例图
校验保存重复文件时

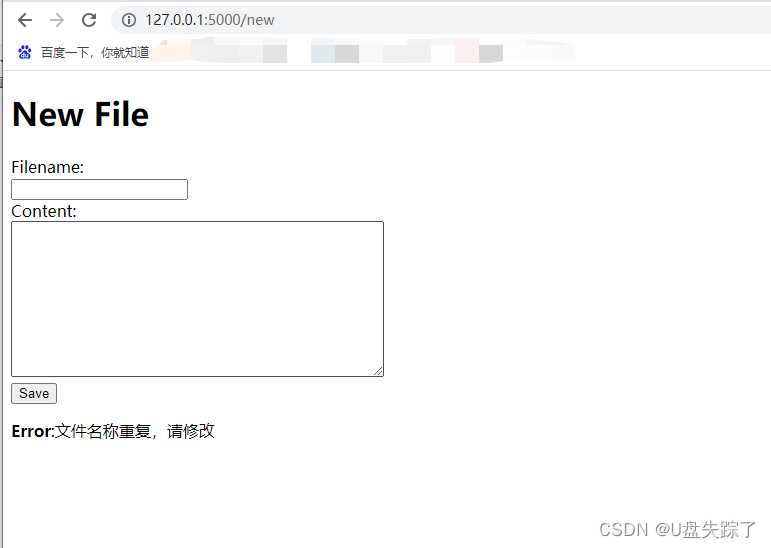
新增文件成功时