前言

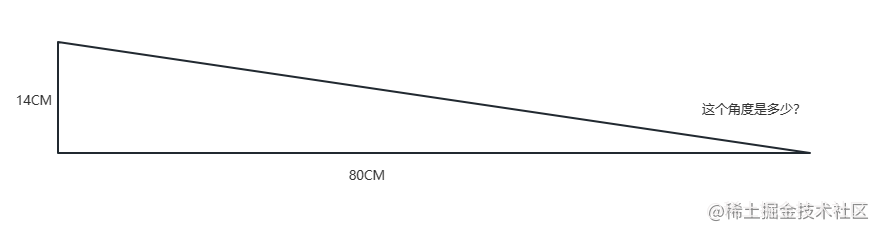
事件是这样的，前几天有人想买个斜坡枕，斜坡枕是个直角三角形，已知短直角边长度是14CM，长直角边长度是80CM，他想知道这个斜坡是多少度，我说这个不是很简单吗？计算一下$arctan(\frac{14}{80})$不就行了吗？

然后我打开苹果计算器，切到的科学计算模式，依次输入14、$÷$ 、80、tanh，一看结果让我有点懵，为什么是0.17323525…？这个坡度肯定不对，应该是我使用错误了，于是花了一点时间研究了一下这个科学计算怎么使用。

角度与弧度

在计算器最左下角有个Rad，点一下会变成Deg，这个就是RAD是Radian的缩写,意为"弧度制(度量角大小的一个单位,30°=π/6,60°=π/3,90°=π/2,180°=π)“,DEG是"Degree"的缩写,意为"角度制”，这个计算时要注意了。

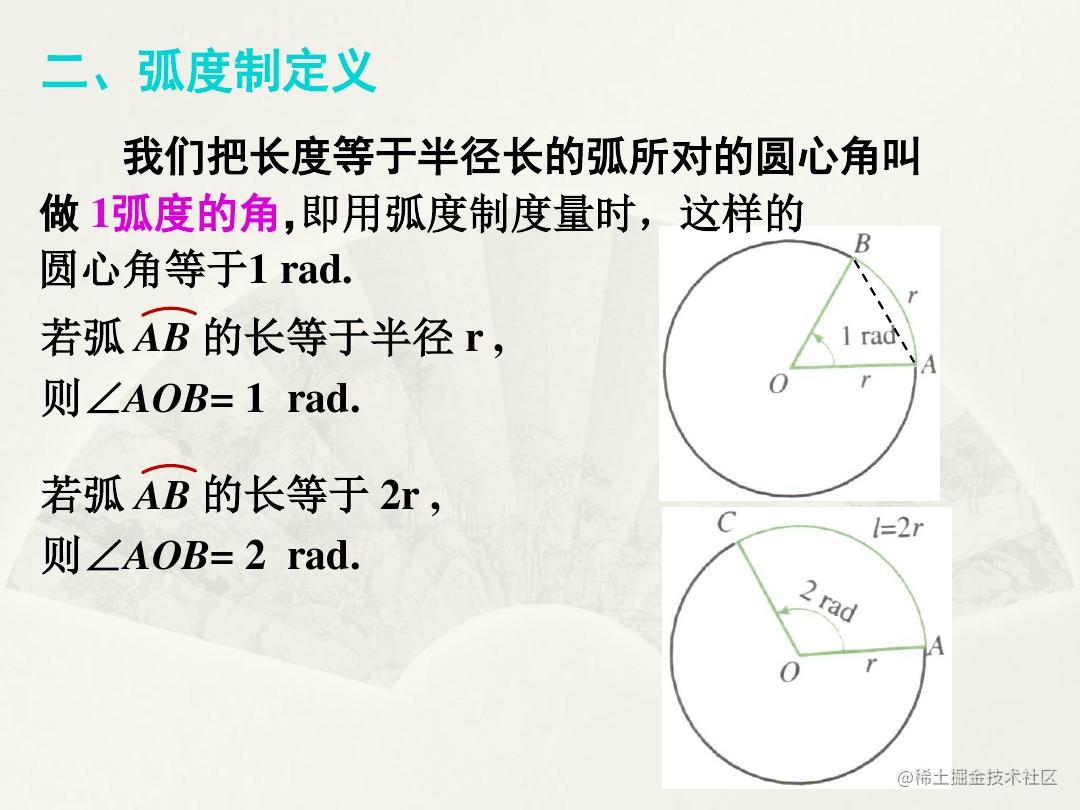
弧度制的定义

tanh双曲正切函数

然后我查一下苹果的文档tanh是双曲正切函数:$tanh(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}$，并不是我们要的反正切函数

$ta{n}^{-1}$反正切函数

在计算机左上方有个 $2^{nd}$，我们按一下，就出现了$ta{n}^{-1}$，这个才是我们要的函数

然后依次输入14、$÷$ 、80、$ta{n}^{-1}$，结果近10°，这个数值应该是对的。

Rand、EE函数、x!

Rand是生成(0,1)之间的随机数

EE是：$x\times 10^y$，比如我们要输入2千万，可以输入2、EE、6

x!是阶乘 $x!=1\times 2\times 3\times ...\times x$

mc、mc+、mc-、mr

这四个主要是操作记忆数值用的，记忆数值默认值为0

• mc (Memory Clear) 用于清除记忆器中存储的数字值
• m+ (Memory Plus) 用于将当前显示的数字值添加到记忆器中存储的数字值之上
• m- (Memory Minus) 用于将记忆器中存储的数字值减去当前显示的数字值
• mr (Memory Recall)用于显示记忆器中存储的数字值

比如我们要计算 (1+2+3+4)-(123*4)
我们可以按 1 + 2 + 3 + 4 m+ 4 x! m- mr
这里1+2+3+4后等于10 按下m+ 将10记忆，$4！=1\times 2\times 3\times 4=24$ ，按下m-后将10-24=-14 记忆下来， 最后按mr显示-14，最后按一下mc清除记忆数值。

$x^y和y^x$

这个就是先后顺序一不样，比如要计算 $2^3$ ，可以按 2、$x^y$、3 也可以按 3、$y^x$、2

总结

本文主要介绍苹果计算器不常用的功能，看似很简单的事件自己平时不操作，突然操作一下，结果和自己预测的不一样就显得尴尬了，真是书到用时方恨少,事非经过不知难，所以我们还是要 纸上得来终觉浅,绝知此事要躬行。