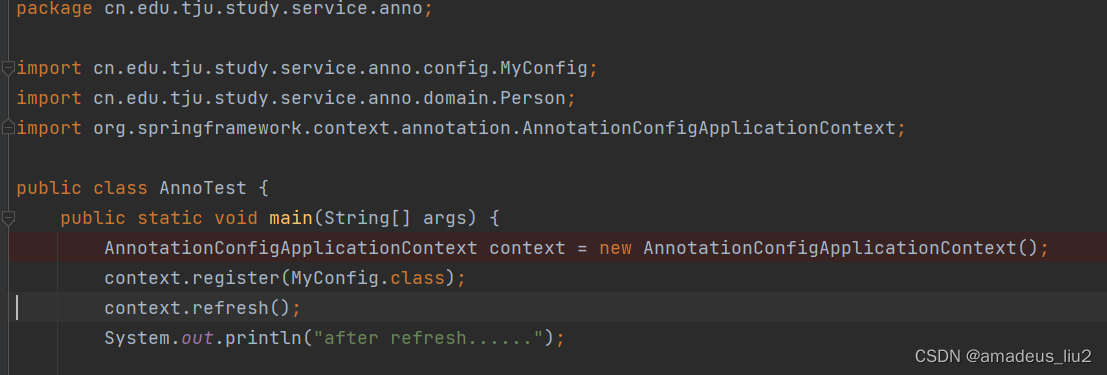
一、主类:
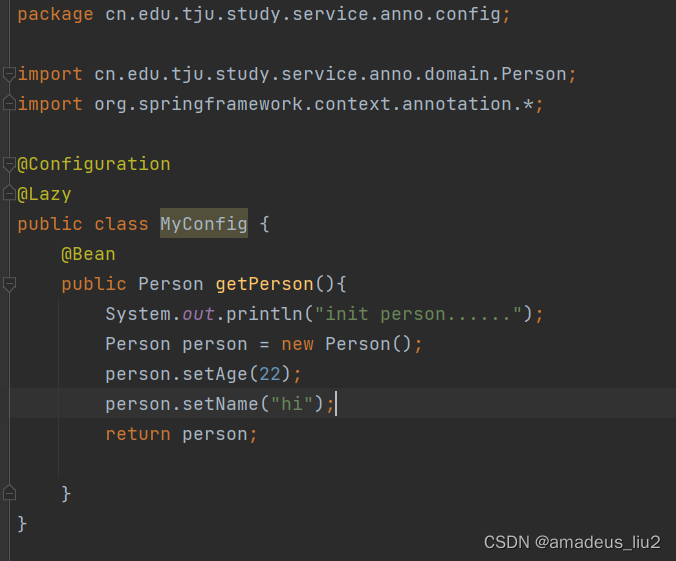
二、配置类:
三、singleton bean的创建流程
运行到context.refresh();

进入refresh方法:
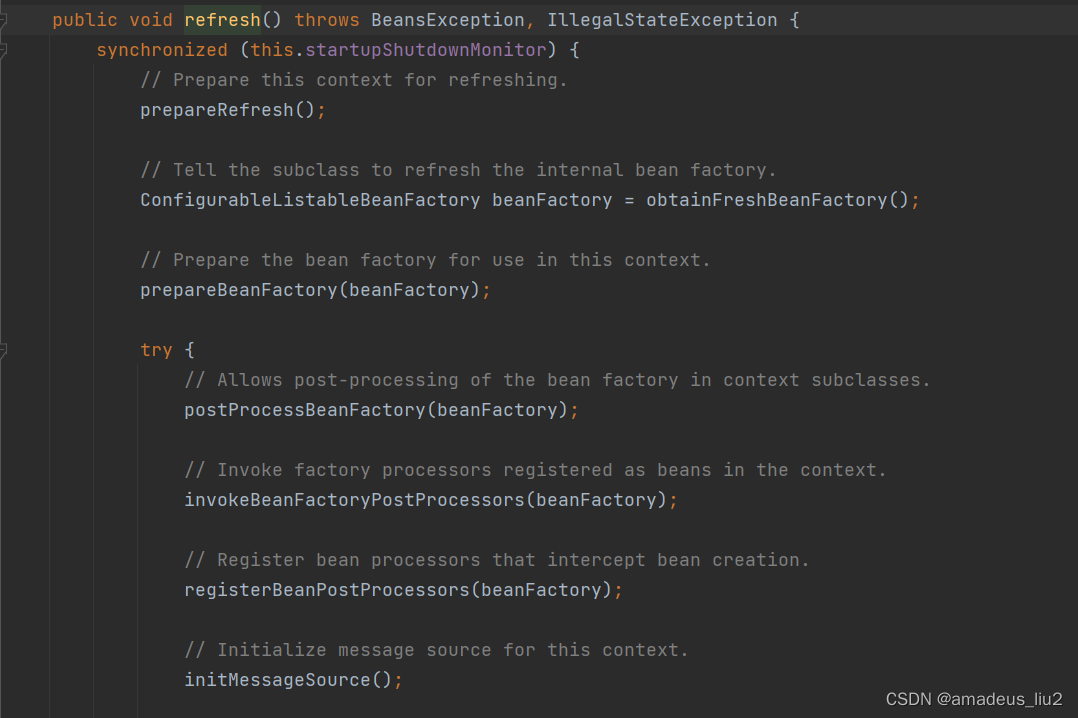
向下运行到红线位置时:
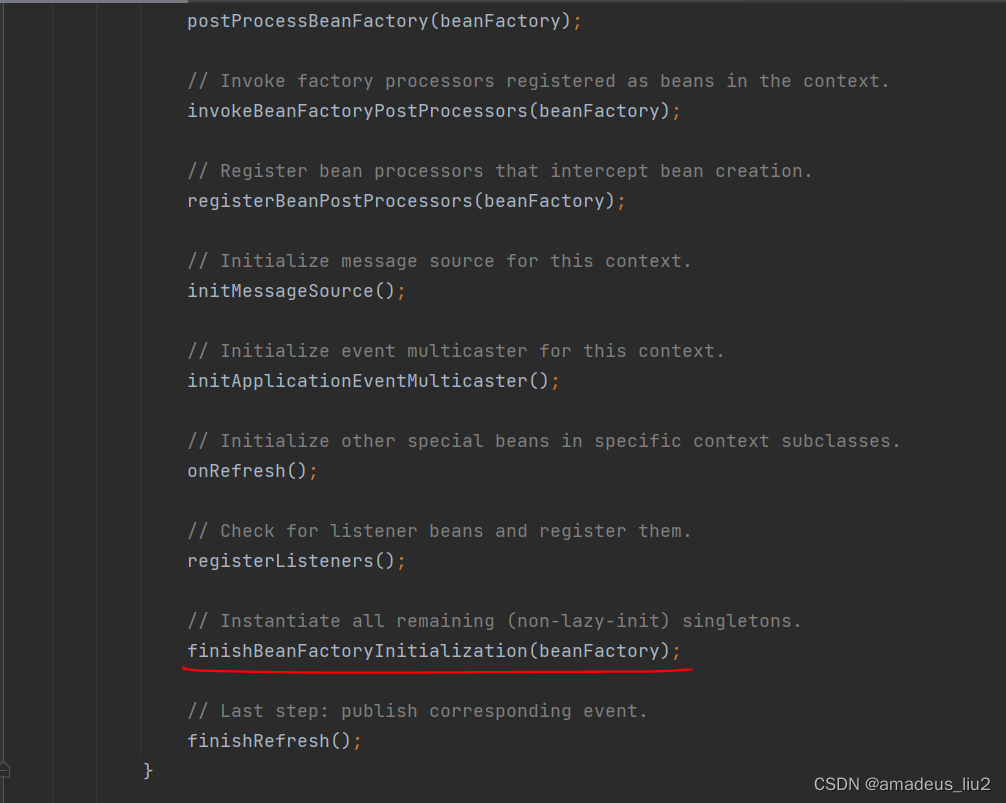
会实例化所有的singleton bean.进入finisheBeanFactoryInitialization方法:
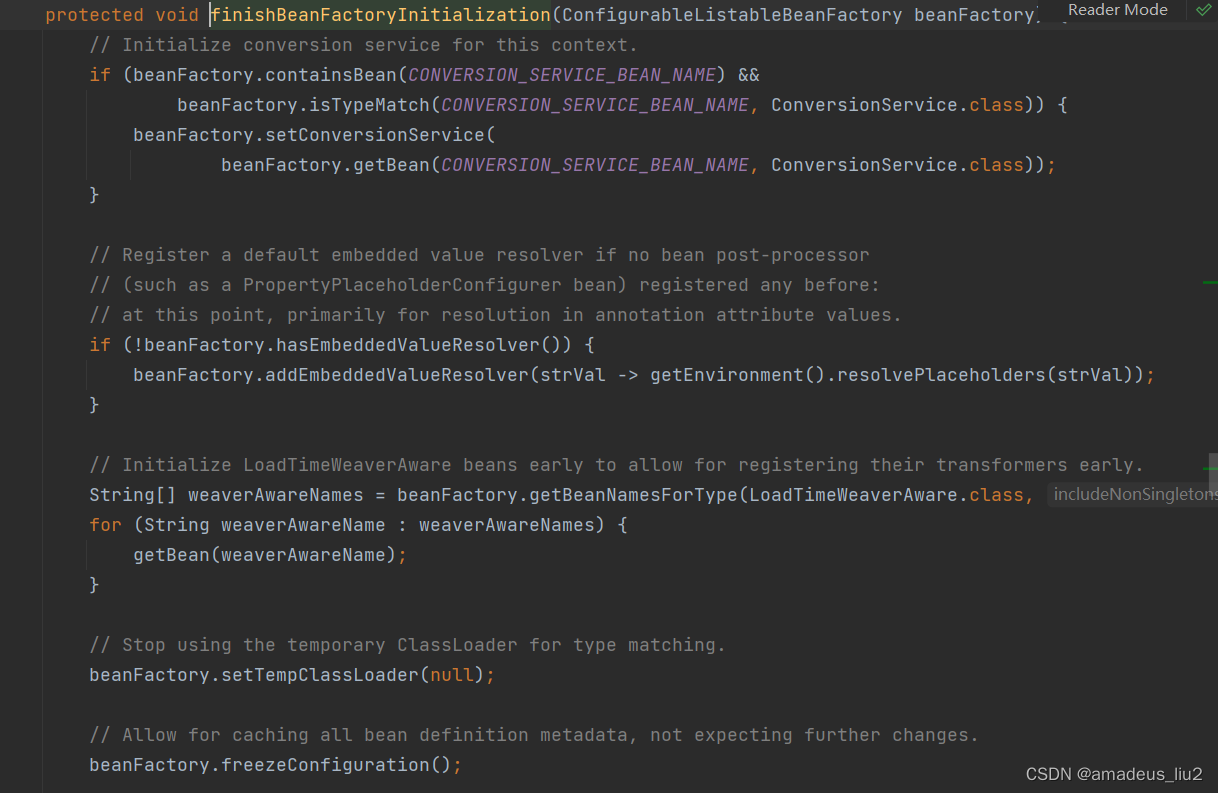
向下拖动代码,可以看到beanFactory.preInstantiateSingletons();
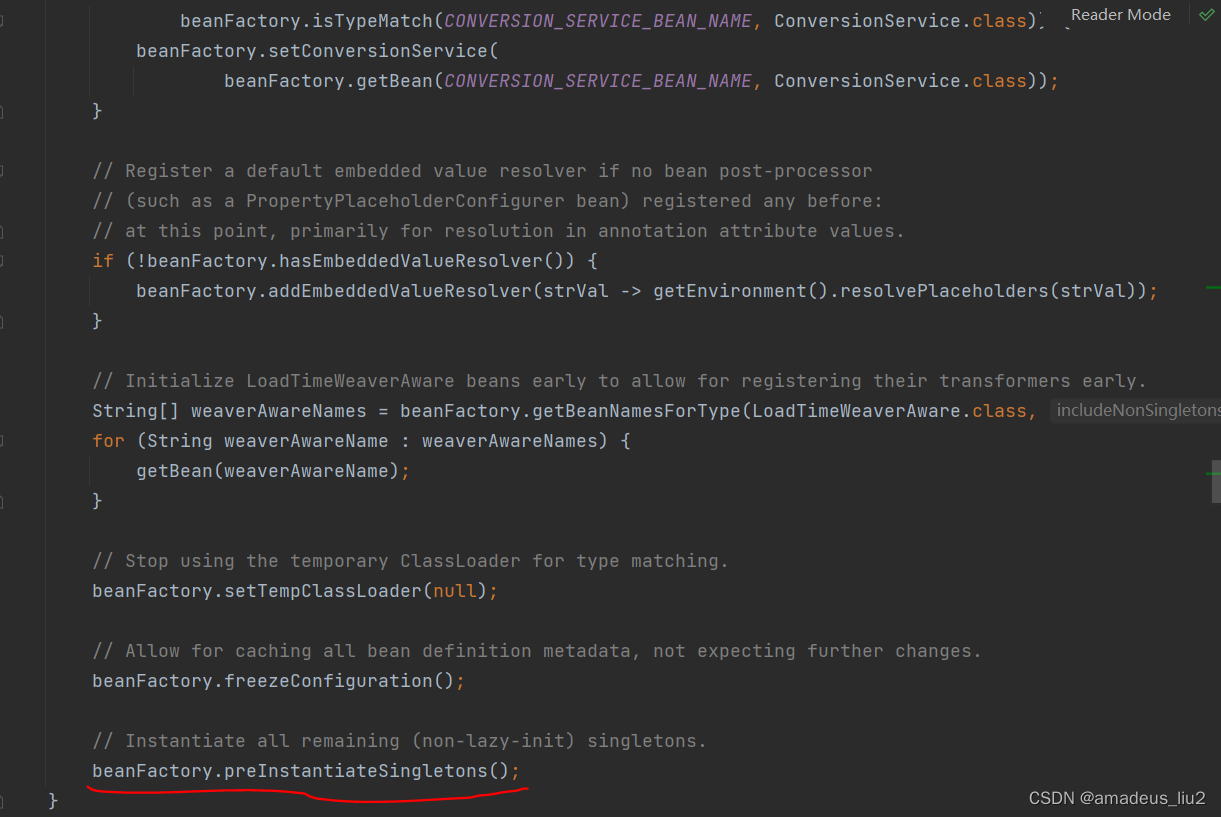
进入preInstantiateSingletons方法:
public void preInstantiateSingletons() throws BeansException {
if (logger.isTraceEnabled()) {
logger.trace("Pre-instantiating singletons in " + this);
}
// Iterate over a copy to allow for init methods which in turn register new bean definitions.
// While this may not be part of the regular factory bootstrap, it does otherwise work fine.
List<String> beanNames = new ArrayList<>(this.beanDefinitionNames);
// Trigger initialization of all non-lazy singleton beans...
for (String beanName : beanNames) {
RootBeanDefinition bd = getMergedLocalBeanDefinition(beanName);
if (!bd.isAbstract() && bd.isSingleton() && !bd.isLazyInit()) {
if (isFactoryBean(beanName)) {
Object bean = getBean(FACTORY_BEAN_PREFIX + beanName);
if (bean instanceof FactoryBean) {
final FactoryBean<?> factory = (FactoryBean<?>) bean;
boolean isEagerInit;
if (System.getSecurityManager() != null && factory instanceof SmartFactoryBean) {
isEagerInit = AccessController.doPrivileged((PrivilegedAction<Boolean>)
((SmartFactoryBean<?>) factory)::isEagerInit,
getAccessControlContext());
}
else {
isEagerInit = (factory instanceof SmartFactoryBean &&
((SmartFactoryBean<?>) factory).isEagerInit());
}
if (isEagerInit) {
getBean(beanName);
}
}
}
else {
getBean(beanName);
}
}
}
// Trigger post-initialization callback for all applicable beans...
for (String beanName : beanNames) {
Object singletonInstance = getSingleton(beanName);
if (singletonInstance instanceof SmartInitializingSingleton) {
final SmartInitializingSingleton smartSingleton = (SmartInitializingSingleton) singletonInstance;
if (System.getSecurityManager() != null) {
AccessController.doPrivileged((PrivilegedAction<Object>) () -> {
smartSingleton.afterSingletonsInstantiated();
return null;
}, getAccessControlContext());
}
else {
smartSingleton.afterSingletonsInstantiated();
}
}
}
}
可以看到实例化singleton bean的代码:
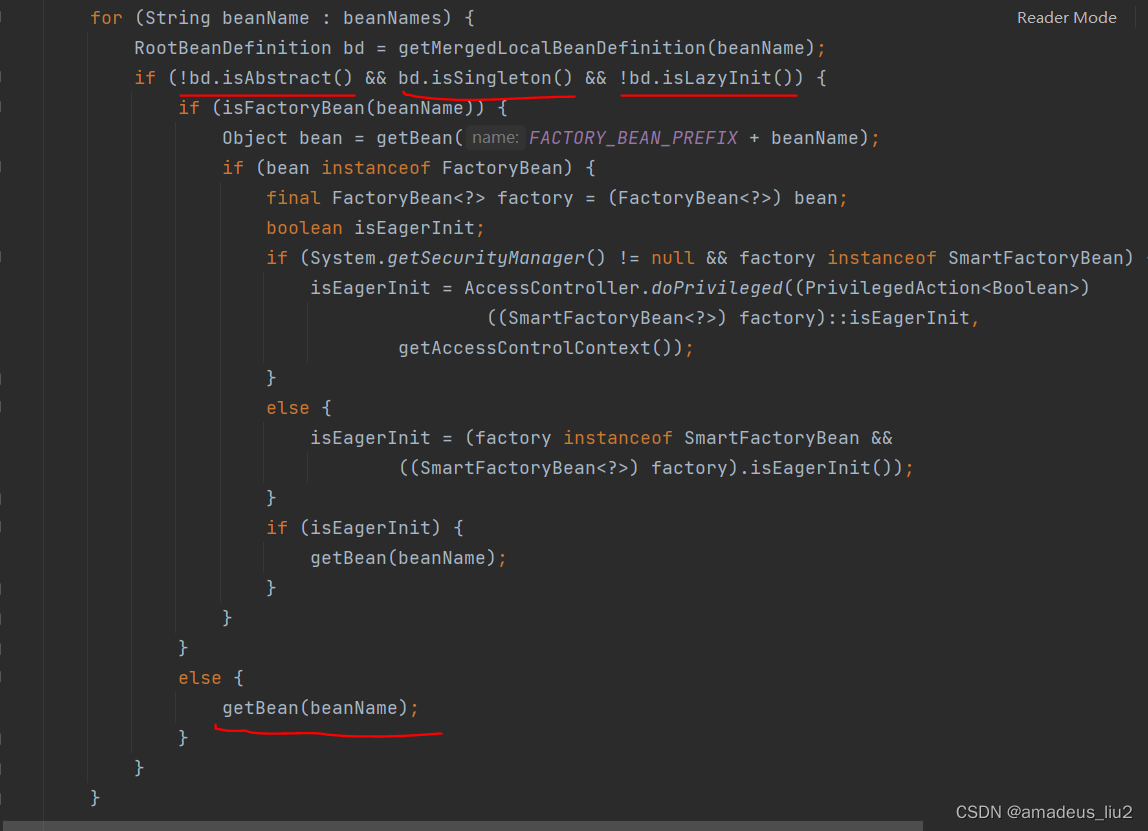
可以看到对非abstract、singleton的、非懒加载的bean,则会调用getBean方法创建bean并缓存(getBean方法的流程不再详述)








![[C初阶]循环和分支语句](https://img-blog.csdnimg.cn/6963e0bd9ece4b559e1020e5d62d49e6.png)
