1、ode23s介绍
ode23s(stiff differential equation solver)是MATLAB中的一种求解刚性(stiff)微分方程的数值方法。刚性微分方程通常具有多个时间尺度差异较大的变量,并且其中至少有一个变量具有快速变化的特性。
ode23s方法使用了一个隐式的一步法(implicit one-step method),结合了 Rosenbrock 方法和 backward differentiation formula (BDF) 方法。这使得 ode23s 在求解刚性问题时具有较高的稳定性和效率。ode23s 可以自动调整步长大小以适应不同阶段的系统行为,并根据需要调整求解器的精度。
此外,ode23s还可以处理非刚性问题,因此它适用于一般的常微分方程组求解。然而,对于非刚性问题,通常可以选择其他更高效的求解器,例如 ode45。
使用 ode23s 求解器,你需要提供微分方程的函数句柄、初值条件以及求解的时间范围。该求解器将返回在给定时间范围内求得的微分方程的解。
2、ode23s用法
Matlab中的ode23s用法为:
[t,y] = ode23s(odefun,tspan,y0)[t,y] = ode23s(odefun,tspan,y0,options)[t,y,te,ye,ie] = ode23s(odefun,tspan,y0,options)sol = ode23s(___)
其中:
[t,y] = ode23s(odefun,tspan,y0)(其中 tspan = [t0 tf])求微分方程组 y′=f(t,y) 从 t0 到 tf 的积分,初始条件为 y0。解数组 y 中的每一行都与列向量 t 中返回的值相对应。
[t,y] = ode23s(odefun,tspan,y0,options) 还使用由 options(使用 odeset 函数创建的参数)定义的积分设置。例如,使用 AbsTol 和 RelTol 选项指定绝对误差容限和相对误差容限,或者使用 Mass 选项提供质量矩阵。
[t,y,te,ye,ie] = ode23s(odefun,tspan,y0,options) 还求 (t,y) 的函数(称为事件函数)在何处为零。在输出中,te 是事件的时间,ye 是事件发生时的解,ie 是触发的事件的索引。
sol = ode23s(___) 返回一个结构体,您可以将该结构体与 deval 结合使用来计算区间 [t0 tf] 中任意点位置的解。您可以使用上述语法中的任何输入参数组合。
3、简单例子
非刚性问题
clcclearclose all% 定义微分方程的函数句柄f = @(t, y) [y(2); -y(1)];% 设置初值条件和求解的时间范围tspan = [0 10];y0 = [0; 1];% 使用 ode23s 求解器求解微分方程[t, y] = ode23s(f, tspan, y0);% 绘制解的图像plot(t, y(:, 1), 'b', t, y(:, 2), 'r');legend('y_1', 'y_2');xlabel('t');ylabel('y');
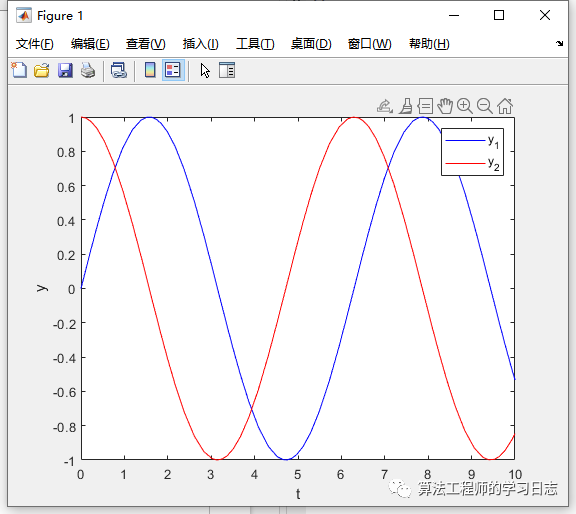
刚性问题
当使用 MATLAB 的 ode23s 求解器来求解刚性问题时,需要提供一个函数句柄来表示微分方程,并设置初始条件和求解的时间范围。
% 定义微分方程的函数句柄f = @(t, y) [-1000*y(1) + 3000*y(2); -3000*y(2) + 2000*y(3); 1000*y(1) - 2000*y(3)];% 设置初值条件和求解的时间范围tspan = [0 1];y0 = [1; 0; 0];% 使用 ode23s 求解器求解微分方程[t, y] = ode23s(f, tspan, y0);% 绘制解的图像plot(t, y(:, 1), 'b', t, y(:, 2), 'r', t, y(:, 3), 'g');legend('y_1', 'y_2', 'y_3');xlabel('t');ylabel('y');
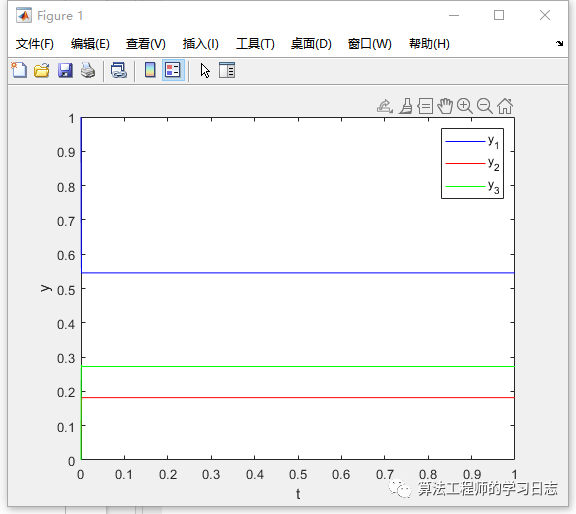
在上述示例中,我们定义了一个刚性的三阶微分方程组,并使用 ode23s 求解器求解该方程组。最后,我们绘制了解的图像,其中 y_1、y_2 和 y_3 分别表示方程组的三个变量。
最后需要注意的是,ode23s 求解器对于一些特定类型的刚性问题可能表现出更好的性能,但对于其他类型的刚性问题可能不如其他求解器(例如 ode15s 或 ode23t)高效。因此,在实际使用中,根据具体问题的性质选择合适的求解器是很重要的。





![[C初阶]循环和分支语句](https://img-blog.csdnimg.cn/6963e0bd9ece4b559e1020e5d62d49e6.png)

![[23] HeadSculpt: Crafting 3D Head Avatars with Text](https://img-blog.csdnimg.cn/420a4790065d45aeac718f711c9f0a9d.png)


