大家好,人工智能近年来变得越来越流行,学习人工智能的需求也随之增加,尤其是许多IT专业人士希望利用机器学习的强大功能,但面临不小的挑战,尤其是在理论和数学上。
步骤1:线性回归
线性回归是一种统计学中常用的回归分析方法,用于建立一个自变量和一个或多个因变量之间的关系模型。在线性回归中,我们假设自变量和因变量之间存在一个线性关系,即因变量的值可以通过对自变量进行线性组合来预测。
线性回归可以用于解决各种问题,例如根据房屋面积、卧室数量、地理位置等因素来预测房价,或者根据广告投入、用户点击率等因素来预测销售额等。
在线性回归中,我们通常使用最小二乘法来估计模型参数,即通过最小化预测值与实际值之间的差异来确定自变量的系数。线性回归还可以通过引入多项式项、交互项等来建立更复杂的模型,以更好地适应实际情况。
下图通过随机生成一些数据,并进行了可视化:
import numpy as np
import matplotlib.pyplot as plt
from helpers import generate_data_lin, plot_linear_model, plot_loss_history
X, y = generate_data_lin(samples=100)
plot_data(X, y)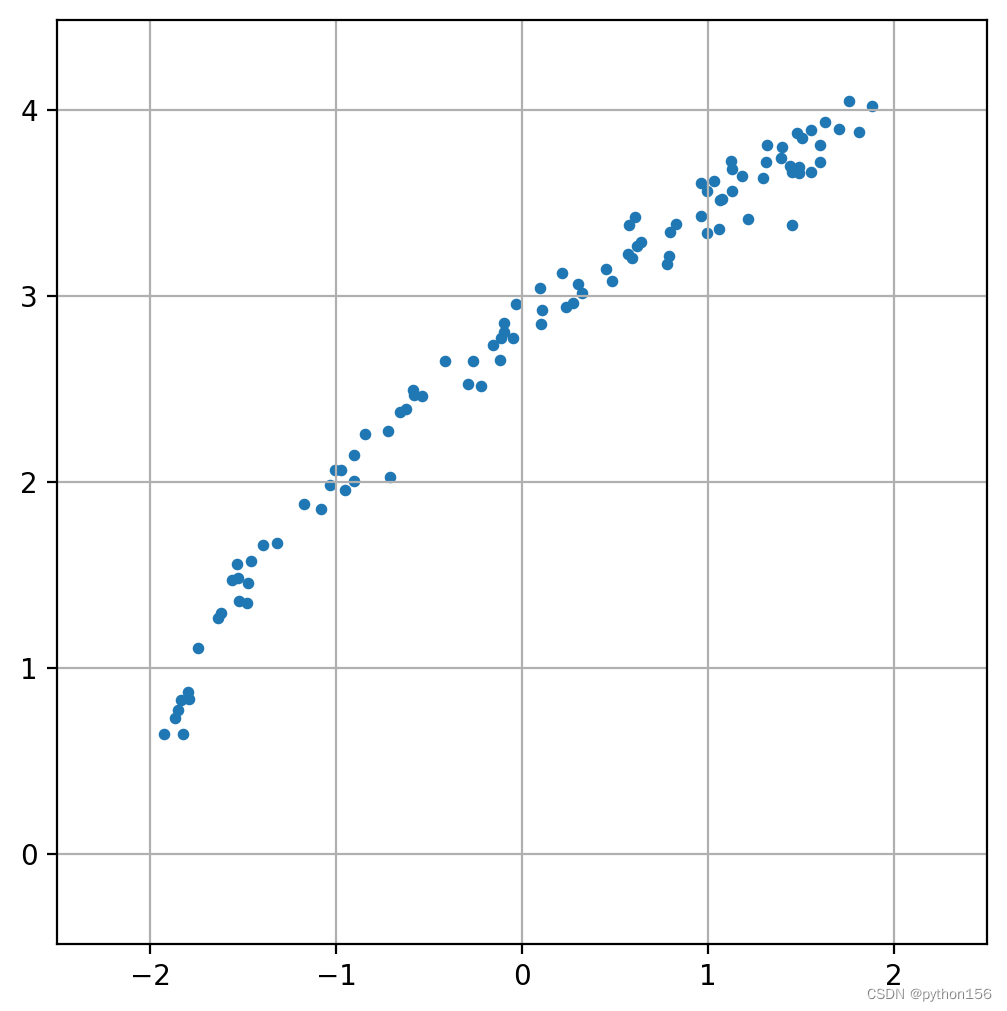
将初始斜率和截距设为0:
# 初始化模型系数
slope = 0
bias = 0
# 绘制未经训练的模型
plot_linear_model(X, y, slope, bias)
实现损失函数、计算模型系数的梯度:
learning_rate = 0.01
epochs = 100
loss_history = []
# TODO: 实现损失函数(MSE)
def loss(X, y, slope, bias):
return 0
# TODO: 计算模型系数的梯度
def gradient(X, y, slope, bias):
return 0, 0
for i in range(epochs):
# 计算梯度
slope_g, bias_g = gradient(X, y, slope, bias)
# 更新系数
slope -= slope_g * learning_rate
bias -= bias_g * learning_rate
# 更新损失历史
loss_history.append(loss(X, y, slope, bias))
plot_linear_model(X, y, slope, bias)
plot_loss_history(loss_history)在这个例子中使用的超参数不多,使用少量的超参数(学习率和周期数)有助于更好地理解它们在训练过程中的作用。
步骤2:多项式回归
从线性回归开始,多项式回归将说明如何添加其他非线性特征(有效地增加模型的复杂性),使我们能够建模更复杂的数据。
由于最终目标是实现神经网络,固定系数的数量可以降低抽象级别。这就是为什么我们通常会使用三次多项式的原因:
![]()
import numpy as np
import matplotlib.pyplot as plt
from helpers import generate_data_poly, plot_poly_model, plot_loss_history
X_train, y_train, X_test, y_test = generate_data_poly(samples=100, test_ratio=0.2)
plot_data(X_train, y_train, X_test, y_test)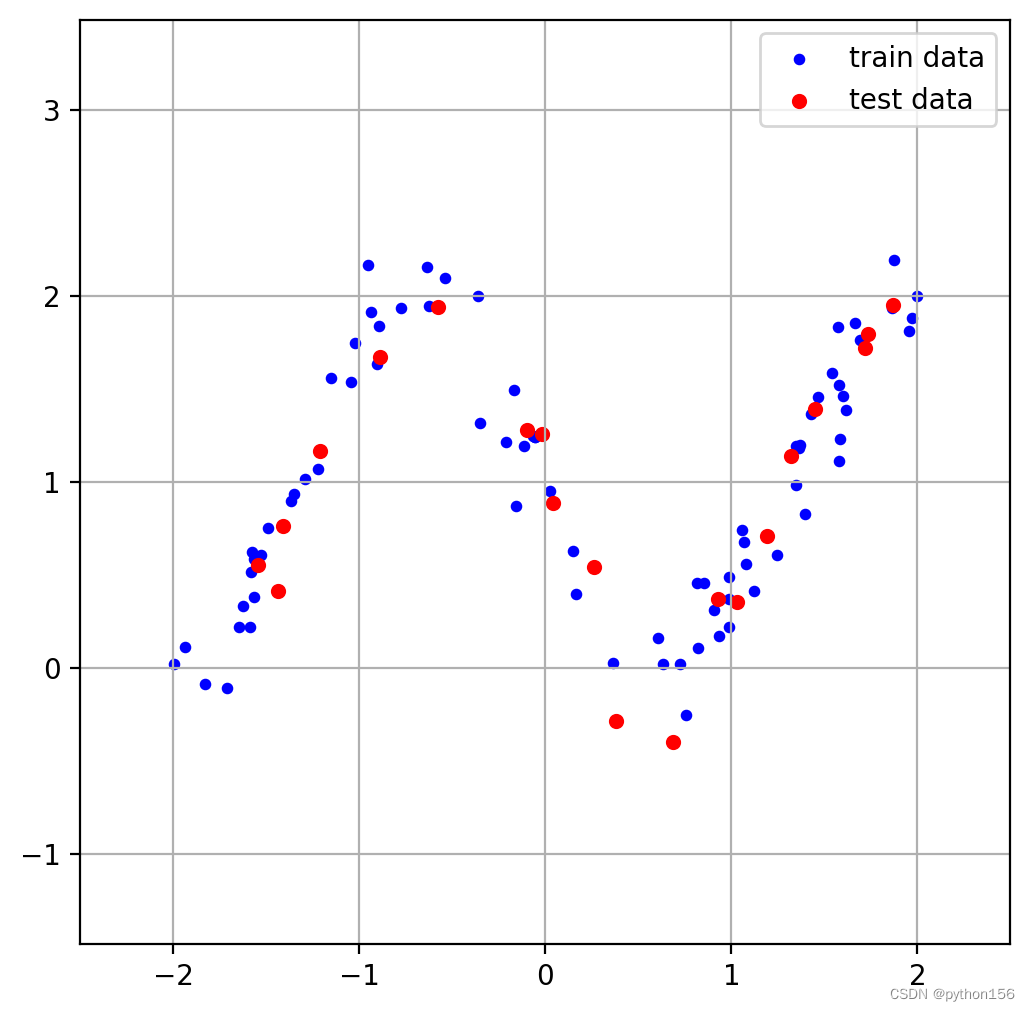
# 用任意的值初始化模型系数
model_coefs = np.array([0, 0.1, 0.1, -0.1])
# 绘制未经训练的模型
plot_poly_model(X_train, y_train, model_coefs)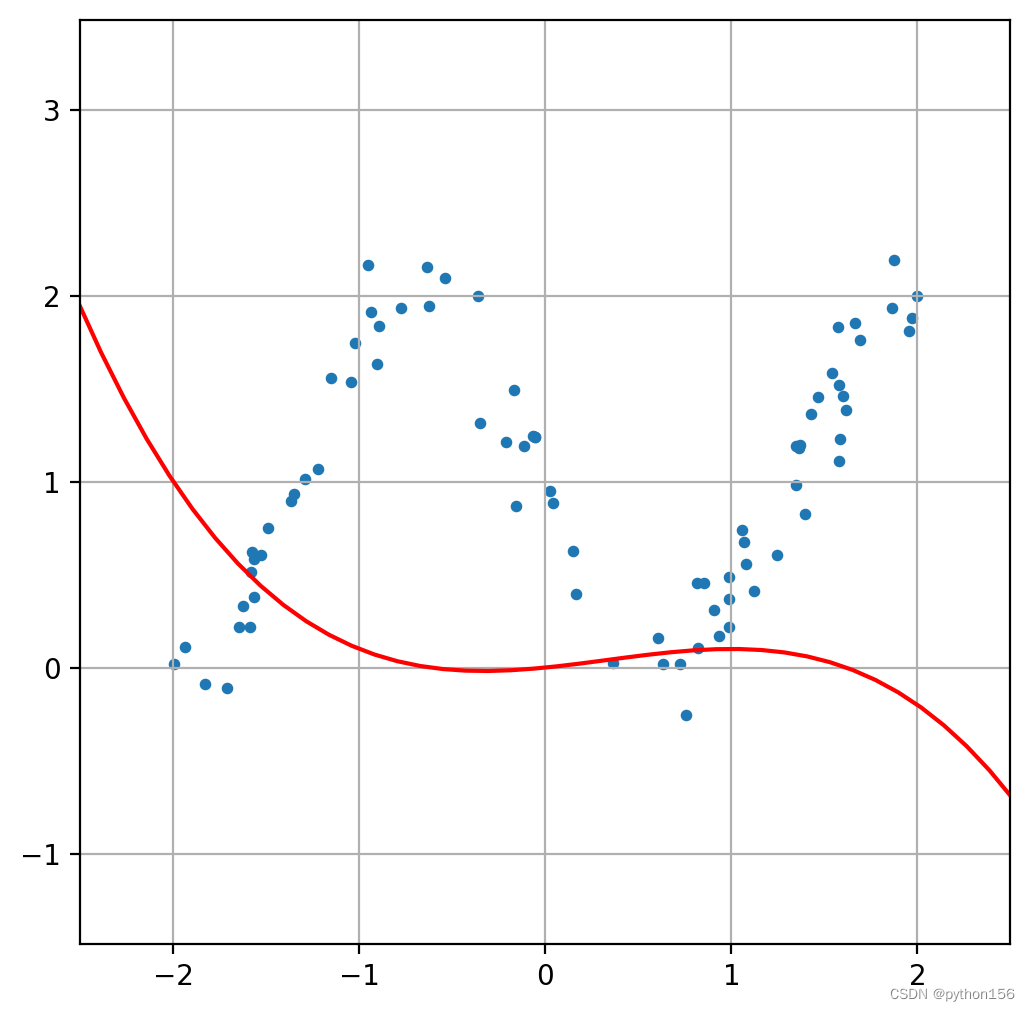
和之前一样,实现损失函数(MSE)并计算模型系数的梯度:
learning_rate = 0.01
epochs = 100
train_loss_history = []
test_loss_history = []
# TODO: 实现损失函数(MSE)
def loss(X, y, model_coefs):
return 0
# TODO: 计算模型系数的梯度
def gradient(X, y, coef):
d0 = 0
d1 = 0
d2 = 0
d3 = 0
return np.array([d0, d1, d2, d3])
for i in range(epochs):
# 计算梯度
coefs_g = gradient(X, y, model_coefs)
# 更新系数
model_coefs -= codefs_g * learning_rate
# 更新损失历史
train_loss_history.append(loss(X_train, y_train, model_coefs))
test_loss_history.append(loss(X_test, y_test, model_coefs))
plot_poly_model(X_test, y_test, model_coefs)
plot_loss_history(train_loss_history, test_loss_history)步骤3:神经网络回归
最后,我们可以基于简单线性回归和多项式回归,从计算图的角度来处理神经网络,可以将神经网络看作手动计算特征的模型。
从三次多项式(四个系数)到具有四个神经元的神经网络的转变非常无缝。这种比较是神经网络可以被视为对任意数量的计算单元(神经元)的抽象的绝佳说明。尽管每个神经元的单独能力较弱,但在数量较大时它们变得非常强大,因为它们使我们能够统一地计算梯度,从而显著地简化了训练过程。
使用TensorFlow创建神经网络模型:
import matplotlib.pyplot as plt
import numpy as np
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Input
from helpers import generate_data_poly, plot_nn_model
X_train, y_train, X_test, y_test = generate_data_poly(samples=100, test_ratio=0.2)
model = Sequential([
Input(1),
Dense(4, activation='relu'),
Dense(1)
])
model.compile(loss='mse')
model.fit(
X_train,
y_train,
epochs=50,
validation_data=[X_test, y_test],
verbose=0
)
plot_nn_model(X_test, y_test, model)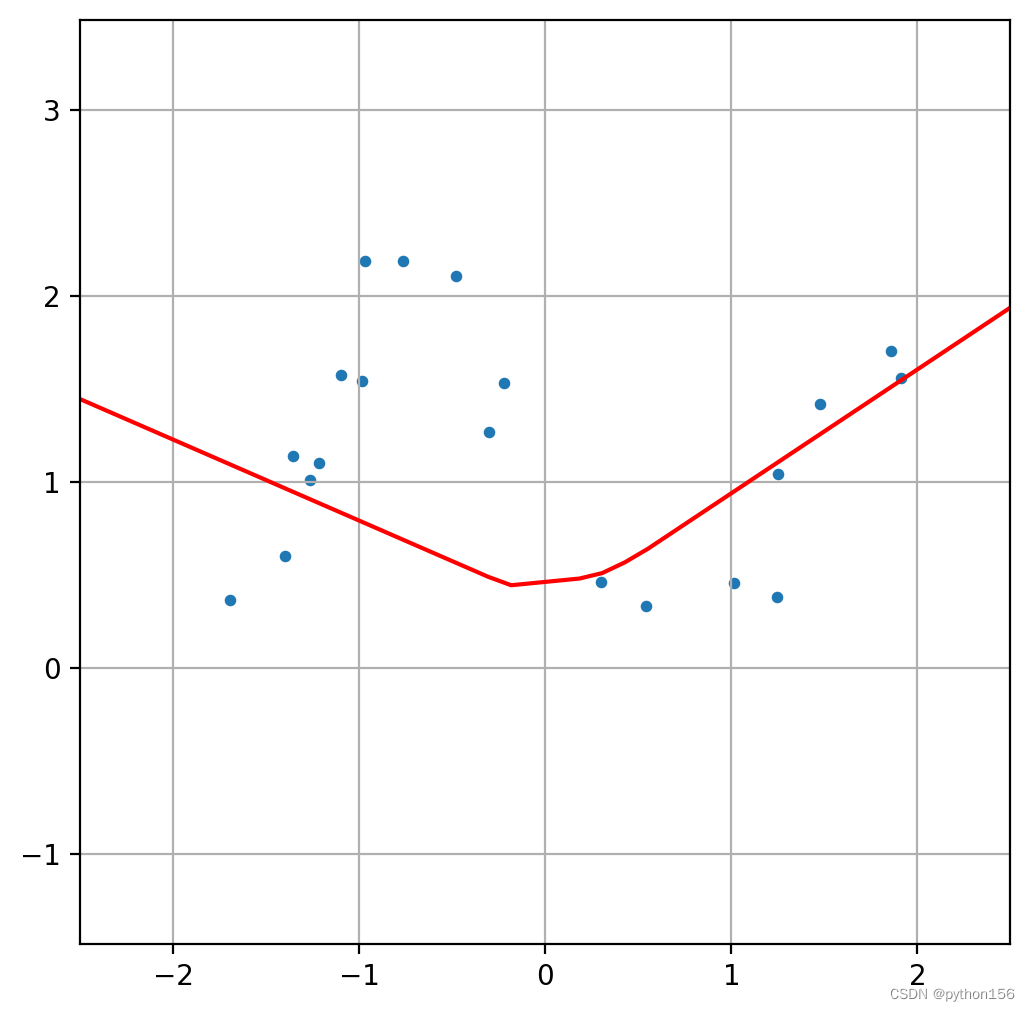
修改模型,使用Dense(32, activation='relu'):
model = Sequential([
Input(1),
Dense(32, activation='relu'),
Dense(1)
])
model.compile(loss='mse')
model.fit(
X_train,
y_train,
epochs=300,
validation_data=[X_test, y_test],
verbose=0
)
plot_nn_model(X_test, y_test, model)
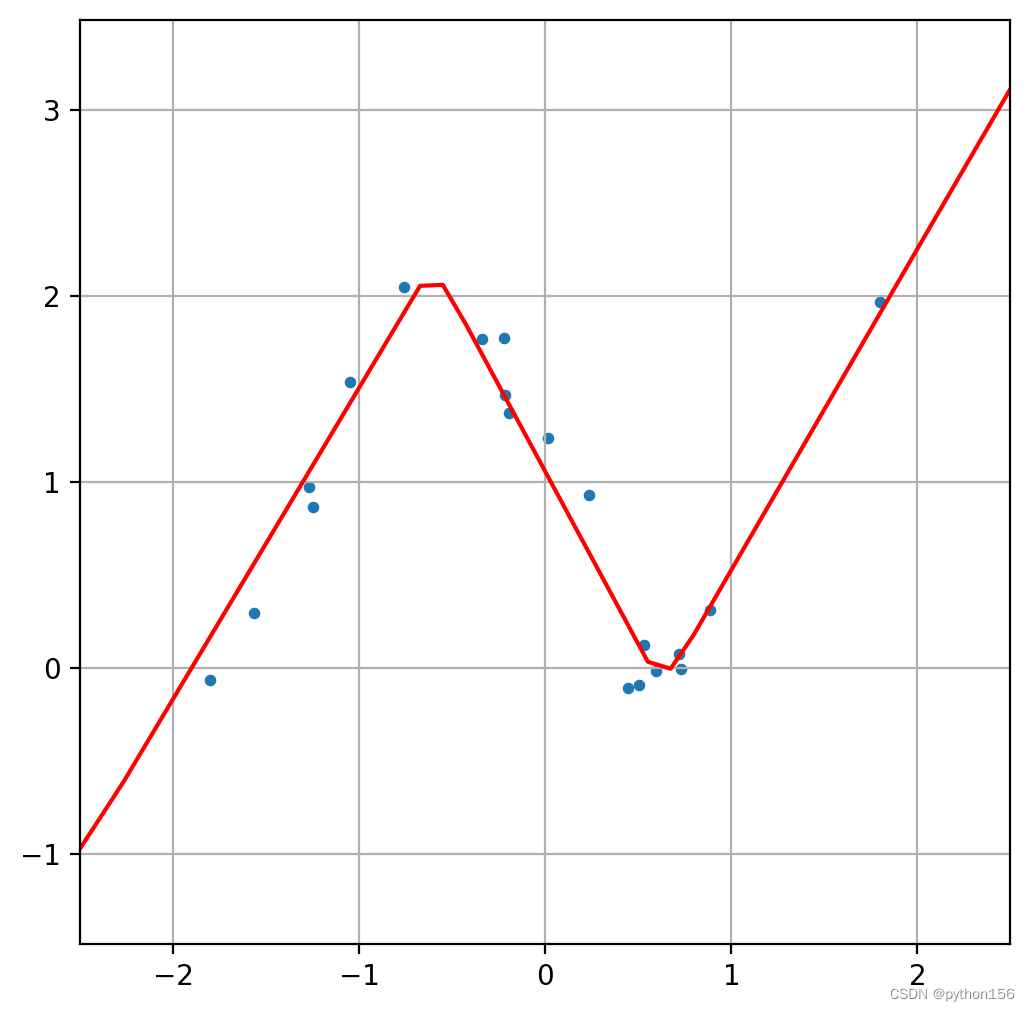
修改模型,再添加一个Dense(16, activation='relu'):
model = Sequential([
Input(1),
Dense(32, activation='relu'),
Dense(16, activation='relu'),
Dense(1)
])
model.compile(loss='mse')
model.fit(
X_train,
y_train,
epochs=300,
validation_data=[X_test, y_test],
verbose=0
)
plot_nn_model(X_test, y_test, model)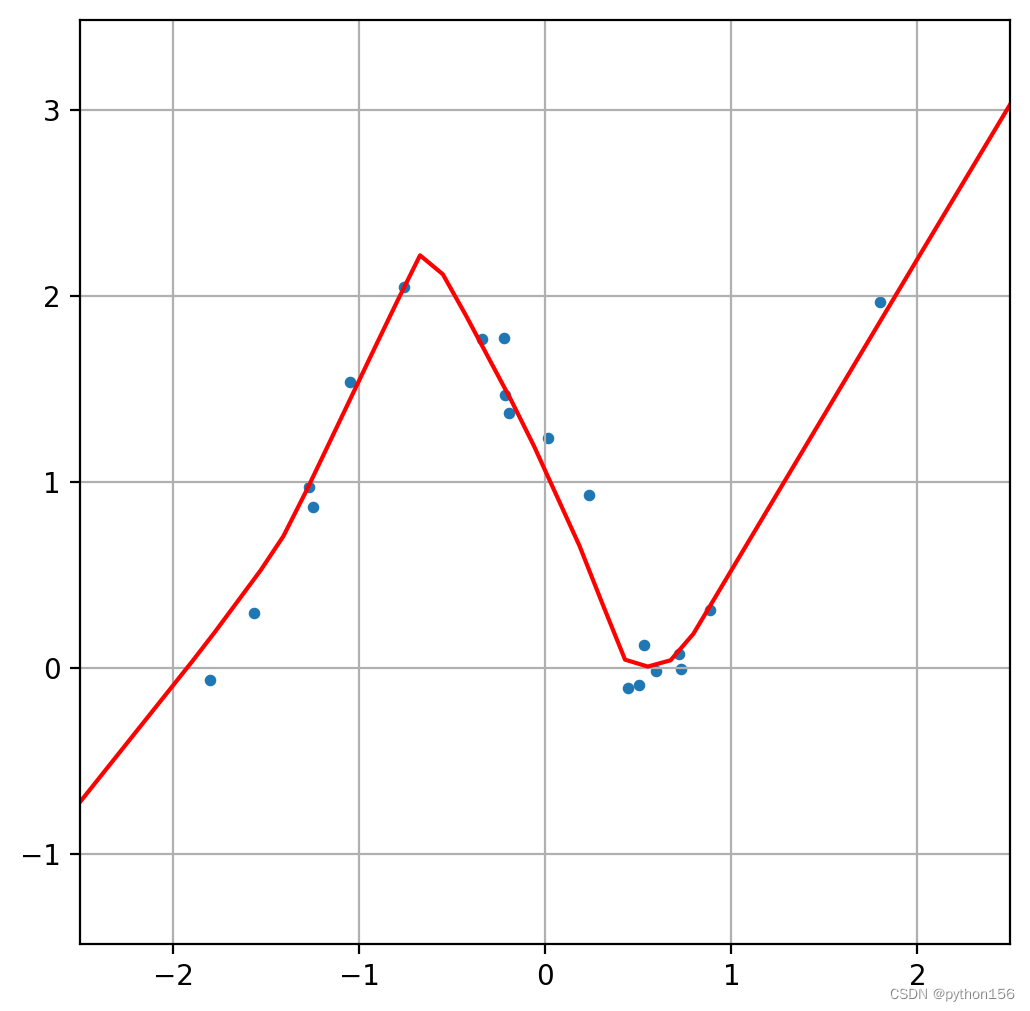
综上所述,在机器学习和统计学中,模型参数是指用来描述模型的一组数值或向量。这些参数可以被调整或优化,以使模型能够更好地拟合训练数据,从而提高模型的预测性能。
模型参数的意义通常取决于具体的模型类型。例如,在线性回归中,模型参数包括自变量的系数和截距项,它们描述了自变量和因变量之间的线性关系。在神经网络中,模型参数包括每个神经元的权重和偏置项,它们描述了神经元之间的连接方式和激活规律。