前言

以无向图为例，介绍与图相关的各种矩阵。我们定义下面的图为 $G$：

import networkx as nx
import matplotlib.pyplot as plt
G = nx.Graph()
G.add_edges_from([(1,2), (2,3), (2,4), (2,5), (3,4), (4,5)]) 
plt.figure(figsize=(5,5))
nx.draw(G, with_labels=True, font_weight='bold', 
        node_size =1000, node_color='cyan', width=2)

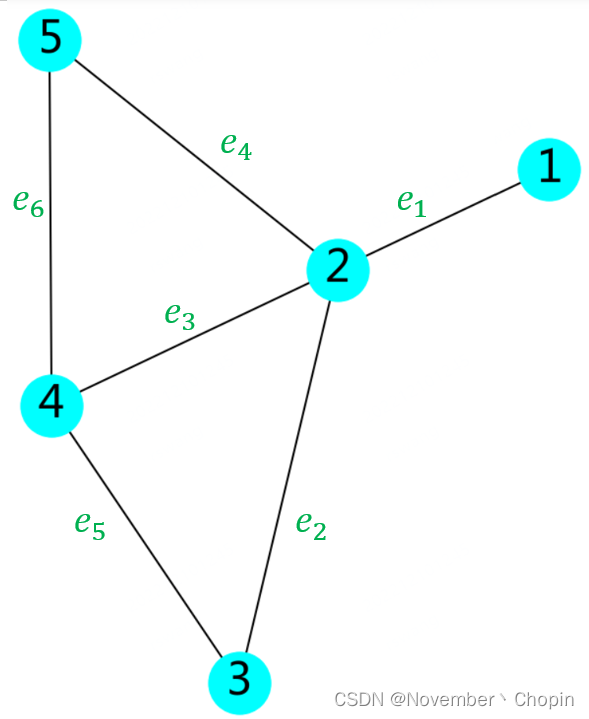
正文

邻接矩阵(Adjacency matrix)

表示顶点之间相邻关系的矩阵，相邻节点在其相应坐标上的值为1。如下所示：
$$A=\left[\begin{array}{ccccc}0& 1& 0& 0& 0\\ 1& 0& 1& 1& 1\\ 0& 1& 0& 1& 0\\ 0& 1& 1& 0& 1\\ 0& 1& 0& 1& 0\end{array}\right]$$

在networkx中的API如下：

A = nx.adjacency_matrix(G).toarray()
print(A)
"""
[[0 1 0 0 0]
 [1 0 1 1 1]
 [0 1 0 1 0]
 [0 1 1 0 1]
 [0 1 0 1 0]]
"""

度矩阵(Degree matrix)

度矩阵是对角阵，对角上的元素为各个顶点的度。如下所示：

$$\begin{array}{c}{D}_{i,j}:=\{\begin{array}{ll}deg(v_i)& \text{if }i=j\\ 0& \text{otherwise}\end{array}\end{array}$$
则 $G$ 的度矩阵为：
$$D=\left[\begin{array}{ccccc}1& 0& 0& 0& 0\\ 0& 4& 0& 0& 0\\ 0& 0& 2& 0& 0\\ 0& 0& 0& 3& 0\\ 0& 0& 0& 0& 2\end{array}\right]$$

networkx没有提供相应的API，不过度矩阵也很容易根据邻接矩阵求出：

D = np.diag(A.sum(0)) # 邻接矩阵在任意轴上的和转换为对角矩阵
print(D)
"""
[[1 0 0 0 0]
 [0 4 0 0 0]
 [0 0 2 0 0]
 [0 0 0 3 0]
 [0 0 0 0 2]]
"""

关联矩阵(Incidence matrix)

关联矩阵将每一行分配给一个节点，将每一列分配给一条边。

	$e_1$	$e_2$	$e_3$	$e_4$	$e_5$	$e_6$
1	1	0	0	0	0	0
2	1	1	1	1	0	0
3	0	1	0	0	1	0
4	0	0	1	0	1	1
5	0	0	0	1	0	1

在networkx中的API如下：

print(nx.incidence_matrix(G).toarray())
"""
[[1. 0. 0. 0. 0. 0.]
 [1. 1. 1. 1. 0. 0.]
 [0. 1. 0. 0. 1. 0.]
 [0. 0. 1. 0. 1. 1.]
 [0. 0. 0. 1. 0. 1.]]
"""

拉普拉斯矩阵

本节介绍几种拉普拉斯矩阵的公式及例子，详细内容参见《关于谱图理论-图傅里叶变换-谱卷积等谱图领域知识的理解》的 Laplacian矩阵简介 一节。

注：由于关联矩阵与邻接矩阵的等价性，拉普拉斯矩阵也可以通过关联矩阵求出，本文只介绍通过邻接矩阵求拉普拉斯的公式，详细内容可参见 wiki百科拉普拉斯矩阵 。

常规拉普拉斯矩阵

$L=D-A$，其中 $D$ 是度矩阵，$A$ 是邻接矩阵。

在networkx中的API如下：

L = nx.laplacian_matrix(G).toarray()
print(L)
"""
[[ 1 -1  0  0  0]
 [-1  4 -1 -1 -1]
 [ 0 -1  2 -1  0]
 [ 0 -1 -1  3 -1]
 [ 0 -1  0 -1  2]]
"""

拉普拉斯矩阵标准化

具有大度数的节点，也称为重节点(heavy node)，会导致拉普拉斯矩阵中的对角线值大的元素支配矩阵属性。标准化旨在通过将拉普拉斯矩阵的条目除以顶点度数，使此类顶点的影响与其他顶点的影响更相等。 为了避免被零除，具有零度数的孤立顶点被排除在标准化过程之外。

$$L^{norm}=D^{-1/2}L{D}^{-1/2}=I-D^{-1/2}A{D}^{-1/2}$$
，其中 $D$ 是度矩阵，$L$ 是邻接矩阵，I是单位矩阵。

numpy计算代码为：

D1 = np.diag(1/np.sqrt(A.sum(0)))  # D^{-1/2}
L_norm = D1.dot(L).dot(D1)
print(L_norm)
"""
[[ 1.         -0.5         0.          0.          0.        ]
 [-0.5         1.         -0.35355339 -0.28867513 -0.35355339]
 [ 0.         -0.35355339  1.         -0.40824829  0.        ]
 [ 0.         -0.28867513 -0.40824829  1.         -0.40824829]
 [ 0.         -0.35355339  0.         -0.40824829  1.        ]]
"""

networkx API为：

L_norm = nx.normalized_laplacian_matrix(G).toarray()
print(L_norm)
"""
[[ 1.         -0.5         0.          0.          0.        ]
 [-0.5         1.         -0.35355339 -0.28867513 -0.35355339]
 [ 0.         -0.35355339  1.         -0.40824829  0.        ]
 [ 0.         -0.28867513 -0.40824829  1.         -0.40824829]
 [ 0.         -0.35355339  0.         -0.40824829  1.        ]]
"""