背景和定义

目前常用的pnp方法有很多，但是本人学习和查阅后发现比较零散，因此，在这里将所学习的方法按照理解分类和总结，并且着重提出实现过程中或者原理上需要注意的点。PnP是Perspective-n-Point的缩写，指在已知相机内参数的前提下，利用某角度下n个三维点与它们对应的图像点坐标，估算出此时拍摄位置的信息。

方法分类

PnP是一类3D-2D对应关系的问题，相似的还有2D-2D，3D-3D关系。
2D-2D关系比如两个视角下拍摄平面物体，根据两幅图像平面上的若干个对应的特征点估算出单应性变换关系；比如对极几何中，左、右相机视图中的点满足极线约束的关系，左图上的一点，利用基础矩阵能够计算出右图的匹配点所在的直线。
3D-3D关系是以三维空间中的坐标系变换为主，在点云拼接中会遇到，比如ICP等。
本文的3D-2D关系，根据背景中提及的，主要用于确定某的图像拍摄的角度，在定位中会经常遇到。
根据PnP原理的不同，按照我个人的理解，将这些方法分为两个大类：
Ⅰ类：通过3D-2D的投影矩阵，直接求解投影方程中的未知数，也就是位姿参数的矩阵
Ⅱ类：通过解算出3D点在相机坐标系下的坐标，结合3D点在世界坐标系的坐标，解算出坐标系转换关系，也就是位姿参数的矩阵

典型方法

P3P(角锥法）

P3P指利用3对3D-2D点来估计相机位姿，解决思路属于第Ⅱ类方法。整体思路为：已知物体点ABC在世界坐标系的坐标，通过他们在图像上的投影点abc，以及光心O构成的三角锥的几何关系，来得到ABC在相机坐标系下的坐标，由此计算出位姿转换矩阵。具体是：

1. 已知a,b,c的图像坐标，计算ab, bc, ac的长度，因为相机的内参是已知的，那么图像点a,b,c在相机坐标系O下的坐标就能得到，由此得到oa, ob,oc的长度，在三角形oab,oac,obc中余弦定理计算∠aoc, ∠aob, ∠boc
   
   
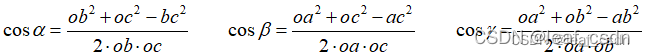
2. 在三角形AOB,AOC,BOC中，同样地能够写出余弦定理表达式，
   方程组中，未知数为OA,OB,OC。这是已知AB、BC、AC长度和三个夹角，计算OA、OB、OC的长度的问题，进一步的吴消元法得到一元四次方程，最终得到4组解析解（详细过程可参见其他博客）。因此，需要第4个点对来验证合适解。解算出这三个量的长度后，又知道oa,ob,oc向量的方向，那么就能得到A,B,C在相机坐标下的坐标.
3. 由ABC在相机坐标系和世界坐标系的坐标，计算转换矩阵（可参考点云对齐）
   

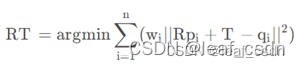
小结：P3P应用时需注意：3个点不共线，实际是要N≥4。

DLT

DLT(direct linear transform)属于第Ⅰ类方法。整体思路为：

1. 根据投影矩阵化简得到关于外参矩阵的两个方程，投影矩阵为
   
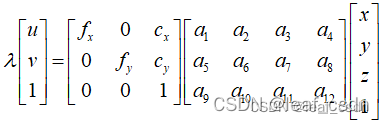
   将矩阵展开，并进一步约去第三项
   
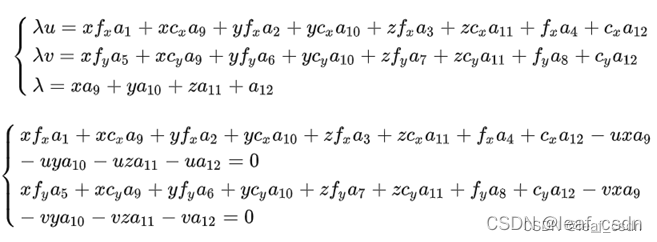
   方程组中未知数为$a_1,a_2,a_3...a_{12}$共12个，由此可见，一对3D-2D点能够建立两个等式，那么至少需要6对这样的点才能解算出12个未知数。
2. 将上面的等式写为矩阵形式，根据至少6对数据，构造“AX=0”形式的方程组，SVD(A)或SVD(ATA)=UWV^T来解算RT矩阵中的12个参数（具体可参见OpenCV内部函数cvFindExtrinsicCameraParams2解析（二））。由式子可以看出，系数矩阵中假如z=0，将会有3列系数都为0，该系数矩阵将不是满秩的矩阵，结果会不稳定，因此，数据不能共面；其次，系数矩阵中的数据来自于世界坐标和像平面坐标，但数据值差异很大时会导致矩阵内的元素差异很大，导致求解出问题，因此通常需要数据归一化处理，可参见多视图几何。
   
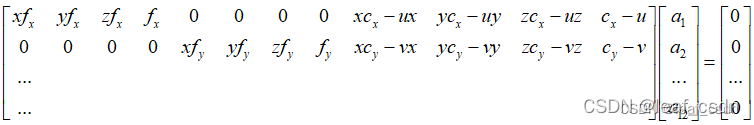
3. SVD解算V的最后一列向量得到RT参数没有尺度信息，需要进一步的处理才能得到满足单位正交特性的旋转矩阵
   
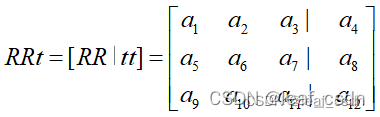
   为了得到正解matR, 可以认为是寻找近似解
   
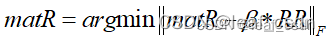
   最优解为
   
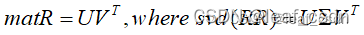
   那么尺度和平移量分别为
   

小结：DLT应用时需注意：所有点不能共面，N≥6，要做数据归一化；SVD的结果还需要进一步分解才能估算得到最终的位姿矩阵

单应性矩阵分解

前面说PnP是3D-2D的问题，若3D点共面，将变为2D-2D问题，可以通过平面的单应性性质来估算位姿参数，重点是单应性矩阵如何分解为R,T。具体可参见另一篇博客Opencv外参估计cvFindExtrinsicCameraParams2原理解析（三），该方法属于第Ⅰ类方法。

1. 两个平面上具有的2D-2D对应点，满足平面单应性关系，单应性矩阵有8个自由度，一对2D-2D点能构成两个方程组，至少需要4对点解算出单应性矩阵。
   
2. 参考张正友的文献，假设世界坐标系在平面上，Z轴垂直于平面，那么平面上点的Z=0。根据投影方程表达为（ORB-SLAM中有Faugeras 的单应性矩阵分解方法, opencv也有实现函数，还未研究）
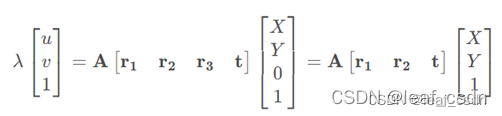   投影方程的输入和输出都是二维点，那么求解的单应性矩阵满足
   
3. 为了满足旋转矩阵列是单位向量性质，根据单应性矩阵的向量做单位化得到r1和r2向量
   
4. 为了满足旋转矩阵正交性质，r1和r2叉乘得到r3向量
   
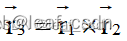
5. 单应性矩阵与外参矩阵存在的系数关系，该系数折中的取
   
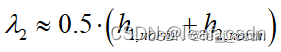
6. 平移向量为
   

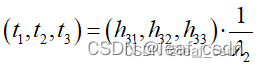
小结：应用时需注意：所有点需要共面，N≥4，重点是如何由单应性分解出旋转和平移量

迭代法

迭代法实现的思路与opencv标定时，对外参数进行初始值估计时使用的迭代法相同，重点在于求解6个外参数的偏导数，具体可参见我的博客外参数求偏导。该方法属于第Ⅰ类方法。
根据投影矩阵，建立投影点与真实点的残差，以最小化投影残差为目标，优化计算RT

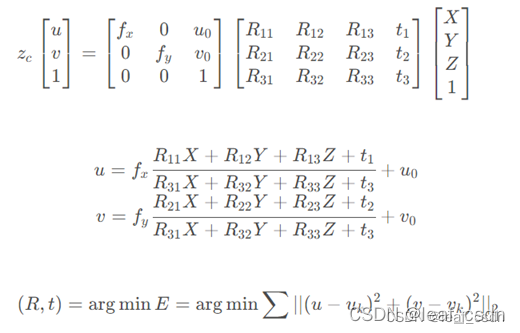
小结：应用时需注意：需要较好的初始值，通常会在之前方法的基础上应用迭代法，所以N取决于初始值的方法

EPnP

E是efficient的缩写，高效性主要体现在第4步所阐述。该方法属于第Ⅱ类方法。整体思路为：

1. 由世界坐标系的3D点得到四个控制点Cj（一个质心，三个主方向上的点），控制点建立质心坐标系，其他的点都能用该四个点加权表示。一个重要的结论是：无论在世界坐标系，还是相机坐标系，权重系数是不变的。那么只要能够求解出在相机坐标下这4个控制点的坐标，带入相同的权重系数，就能计算任意点在相机坐标系的位置，从而转换为3D-3D坐标系变换问题。
   

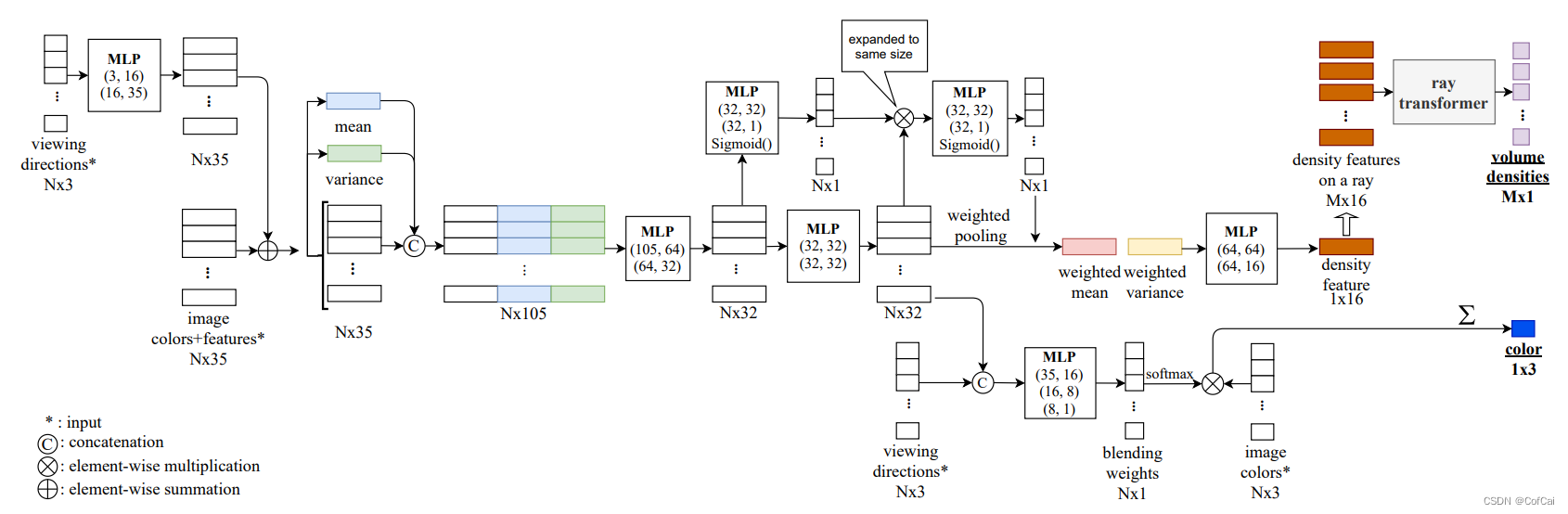
2. 为了求解这4个点的相机坐标系的位置，如下左图根据投影矩阵展开得到两个等式：已知数是内参数和权重系数，未知数是四个控制点的三维坐标（共12个未知数），因此至少要6对点来进行求解。
   

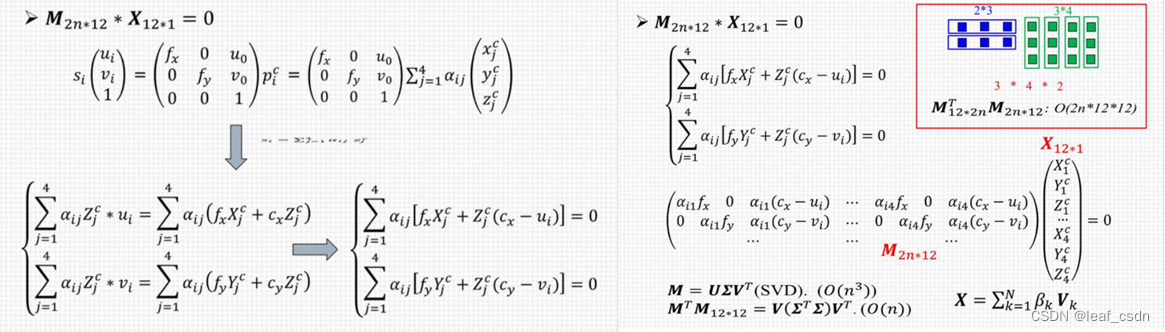
3. 对于上面形如AX=0的解，SVD分解A系数矩阵，V的最后一列是特征值最小的零空间向量，也就是方程的解。我们知道对于12个未知数的方程组，至少要6对点来能求解，原文之所以N在4到6也可以计算，个人认为是包含了一个隐含条件，那就是焦距足够大，下图是原文在随着焦距增大时，SVD最小的4个特征值是接近0的，因此能够用V最后1~4列的向量来加权表示AX=0的解。
   

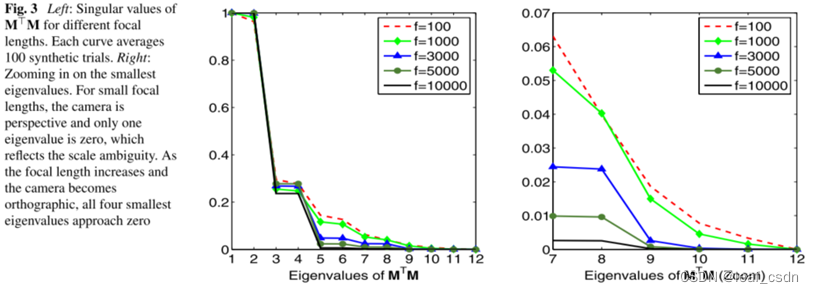
4. 进一步用高斯牛顿迭代，对上述中“用V最后1~4列的向量来加权表示AX=0的解”中的权重计算最优解，细化求解相机坐标系下的控制点坐标。这里，EPNP的高效主要是算法复杂度为O(n）,并且高斯牛顿迭代过程相对于传统的迭代法来说参数更少，至多4个权重系数，而迭代法为6个外参数，收敛更快。这也就是我对高效性的理解。
   

5. 由Pi在相机坐标系和世界坐标系的坐标，计算转换矩阵。

小结：应用时需注意： N≥4，但实际应用N≥6才算稳定

其他延伸

**延申1：**在未知相机内参数的情况下，诸多方法也能适用，但解算的稳定性不同，如UPnP(Uncalibrated PnP),求解过程与EPnP相似，只是在求解控制点在相机坐标系的坐标时，建立方程组将焦距也作为未知数

**延申2：**通常内参和外参都未知时，根据3D-2D点得到了内参外参组合的摄像机矩阵，需要进一步分解内参矩阵和外参矩阵，这里需要利用内参矩阵的上三角特点，利用RQ分解来得到内参K，外参R和t摄像机矩阵的分解

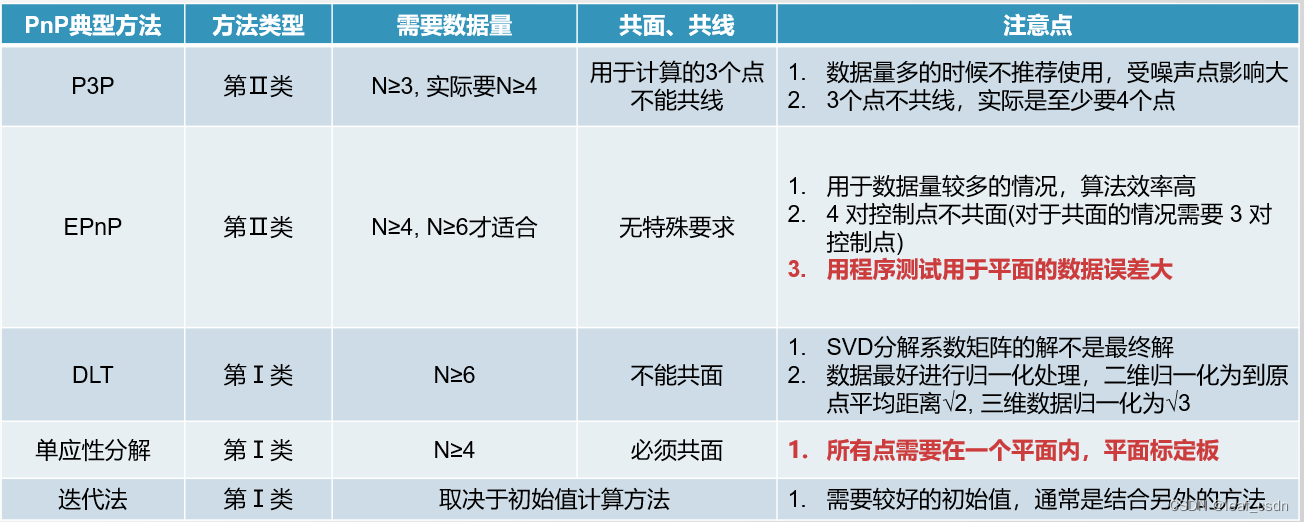
总结

最后是对上面所有提及方法的一个总结，通常使用平面标定板在进行相机标定时，会使用到单应性分解+迭代法的组合，我这里测试EPNP时发现在平面数据上结果偏差还是比较大的，后续有分析结果再更新。