文章目录
- 01背包问题
- 完全背包
- 多重背包
- 分组背包
- 背包练习题
- 2. 01背包问题
- 3. 完全背包问题
- 4. 多重背包问题 I
- 5. 多重背包问题 II
- 9. 分组背包问题
01背包问题
n个物品,每个物品的体积为
v
i
v_i
vi,价值为
w
i
w_i
wi,每次只能选择一个物品放入背包
在背包能装下的情况下,价值最大的装法?
每个物品最多只能使用1次

dp问题从两方面考虑,状态表示与状态计算
状态表示:每个状态都可以用不同的维度描述,01背包问题中,每种选法对应不同的状态,设
f
(
i
,
j
)
f(i, j)
f(i,j)为状态
- 集合:所有的状态构成了一个集合,也就是所有的选法构成了一个集合
- 考虑集合中的状态可以由哪些条件限制,背包问题中有两个条件
- 从前i个物品中选择
- 选择的物品总体积 < = j <= j <=j
- 考虑集合中的状态可以由哪些条件限制,背包问题中有两个条件
- 属性:最大值,最小值,数量,背包问题的属性为最大值
状态表示从两个方面考虑,集合以及集合的属性。根据题意,将所有状态(选择)看成集合,同时用条件限制集合中的状态。也就是将状态用条件表示出来,同时根据题意思考集合(状态)表示的含义,也就是属性。一般的属性有最大值,最小值以及数量
状态计算:常说的状态转移方程,本质就是集合的划分,如何将集合划分成更小的子集,同时保证子集中的元素不重不漏?
最常用的思考角度是:选择某一条件,不具有该条件为一个集合,具有该条件为一个集合
在01背包问题中,可以考虑不选择第i个物品以及选择第i个物品为两个不同集合,这两个不同集合构成了状态
f
(
i
,
j
)
f(i, j)
f(i,j)
- 不选择第i个物品时,集合的含义是:从前i个物品中选择,但不选择第i个物品,此时能获得的最大价值。可以表述成从前i-1个物品中选择,此时能获得的最大价值。即 f ( i − 1 , j ) f(i-1, j) f(i−1,j)
- 选择第i个物品时,集合的含义是:从前i个物品中选择,且必须选择第i个物品,此时能获得的最大价值。举个例子:若一场考试中,小明考了最高分,将所有人的分数减去10分,小明还是最高分。选择的物品中,注定要选择第i个物品的话,在还未选择第i个物品之前, f ( i , j ) f(i, j) f(i,j)就已经确定。只不过我们需要加上限制,从 f ( i − 1 , j − v i ) f(i-1, j - v_i) f(i−1,j−vi)中推导。为什么需要这个限制?很显然,最高分加上成绩后不能超过上限,最低分减去成绩后不能低过下限
先把所有物品中的第i个物品去掉,求出此时的最大值,然后加上第i个物品的价值
由于所有的选法都包含第i个物品,要求从1i个物品中选择物品的最大价值时,可以将每种选法的第i个物品都去掉,此时的最大价值加上第i个物品的价值也是从1n个物品中选择物品的最大价值
那么状态就变成了从1~i - 1个物品中选,并且体积不超过v-
v
i
v_i
vi的最大价值
f
(
i
−
1.
j
−
v
i
)
+
w
i
f(i - 1. j - v_i) + w_i
f(i−1.j−vi)+wi
最后两个集合不重不漏构成了
f
(
i
,
j
)
f(i, j)
f(i,j)这个集合,由于集合的属性是选择的最大价值,所以
f
(
i
,
j
)
=
m
a
x
(
f
(
i
−
1
,
j
)
,
f
(
i
−
1
,
j
−
v
i
)
+
w
i
)
f(i, j) = max(f(i-1, j), f(i-1, j-v_i)+w_i)
f(i,j)=max(f(i−1,j),f(i−1,j−vi)+wi)
同时考虑初始状态,
f
(
i
,
0
)
=
0
f(i, 0) = 0
f(i,0)=0:背包容量为0时,无法装入物品,所以总价值为0
f
(
0
,
i
)
=
0
f(0, i) = 0
f(0,i)=0,从前0个物品中选择物品装入背包,此时的总价值也为0
完全背包
与01背包不同,每个物品能使用无限次
状态表示与01背包相同,不同的是状态计算
如何划分
f
(
i
,
j
)
f(i, j)
f(i,j)这个集合?依然是从两个方面,选择第i个物品以及不选择第i个物品
不选择第i个物品时的状态为
f
(
i
−
1
,
j
)
f(i-1, j)
f(i−1,j)
选择第i个物品时,由于物品能选择无限次,直到背包装不下为止,假设背包能装下n个第i个物品,那么此时的状态为
f
(
i
−
1
,
j
−
k
∗
v
i
)
f(i-1, j-k*v_i)
f(i−1,j−k∗vi),其中k从1到n
这些集合不重不漏,组成了
f
(
i
,
j
)
f(i, j)
f(i,j),考虑集合的属性为选择物品的最大价值,所以
f
(
i
,
j
)
=
m
a
x
(
f
(
i
−
1
,
j
)
,
f
(
i
−
1
,
j
−
v
i
)
+
w
i
,
f
(
i
−
1
,
j
−
2
∗
v
i
)
+
2
∗
w
i
,
.
.
.
)
f(i, j) = max(f(i-1, j), f(i-1, j-v_i)+w_i, f(i-1, j-2*v_i)+2*w_i, ...)
f(i,j)=max(f(i−1,j),f(i−1,j−vi)+wi,f(i−1,j−2∗vi)+2∗wi,...)
根据这个表达式,就有了完全背包的朴素解法
for (int i = 1; i <= n; ++ i )
{
for (int j = 1; j <= m; ++ j )
{
for (int k = 0; k * v[i] <= j; ++ k )
{
f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);
}
}
}
printf("%d\n", f[n][m]);
正常情况下,这个做法将超时
f
(
i
,
j
−
v
i
)
=
m
a
x
(
f
(
i
−
1
,
j
−
v
i
)
,
f
(
i
−
1
,
j
−
2
∗
v
i
)
+
w
i
,
f
(
i
−
1
,
j
−
3
∗
v
i
)
+
2
∗
w
i
,
.
.
.
)
f(i, j-v_i) = max(f(i-1, j-v_i), f(i-1, j-2*v_i) + w_i, f(i-1, j-3*v_i) + 2*w_i, ...)
f(i,j−vi)=max(f(i−1,j−vi),f(i−1,j−2∗vi)+wi,f(i−1,j−3∗vi)+2∗wi,...)
将这个状态与
f
(
i
,
j
)
f(i, j)
f(i,j)进行对比:
f
(
i
,
j
)
=
m
a
x
(
f
(
i
−
1
,
j
)
,
f
(
i
−
1
,
j
−
v
i
)
+
w
i
,
f
(
i
−
1
,
j
−
2
∗
v
i
)
+
2
∗
w
i
,
.
.
.
)
f(i, j) = max(f(i-1, j), f(i-1, j-v_i)+w_i, f(i-1, j-2*v_i)+2*w_i, ...)
f(i,j)=max(f(i−1,j),f(i−1,j−vi)+wi,f(i−1,j−2∗vi)+2∗wi,...)
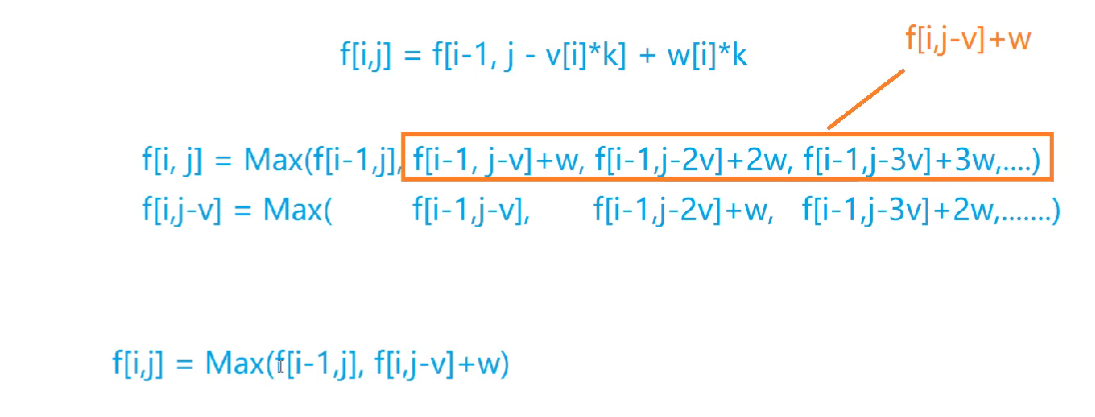
可以得到等式:
f
(
i
,
j
)
=
m
a
x
(
f
(
i
−
1
,
j
)
,
f
(
i
,
j
−
v
i
)
+
w
i
)
f(i, j) = max(f(i-1, j), f(i, j-v_i) + w_i)
f(i,j)=max(f(i−1,j),f(i,j−vi)+wi)
此时线性的枚举就被优化掉,得到一个二维dp
for (int i = 1; i <= n; ++ i )
{
for (int j = 1; j <= m; ++ j )
{
f[i][j] = f[i - 1][j];
if (v[i] <= j) f[i][j] = max(f[i][j], f[i][j - v[i]] + w[i]);
}
}
printf("%d\n", f[n][m]);
压缩后
for (int i = 1; i <= n; ++ i )
for (int j = v[i]; j <= m; ++ j )
f[j] = max(f[j], f[j - v[i]] + w[i]);
printf("%d\n", f[m]);
注意:j不是从后往前更新的,因为在二维dp中
f
[
i
]
[
j
]
=
m
a
x
(
f
[
i
]
[
j
]
,
f
[
i
]
[
j
−
v
[
i
]
]
+
w
[
i
]
)
f[i][j] = max(f[i][j], f[i][j - v[i]] + w[i])
f[i][j]=max(f[i][j],f[i][j−v[i]]+w[i])
其中
f
[
i
]
[
j
−
v
[
i
]
]
+
w
[
i
]
f[i][j - v[i]] + w[i]
f[i][j−v[i]]+w[i]是当前行i的状态,需要先更新
而01背包问题的压缩中,
f
[
i
]
[
j
]
=
m
a
x
(
f
[
i
]
[
j
]
,
f
[
i
−
1
]
[
j
−
v
[
i
]
]
+
w
[
i
]
)
f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i])
f[i][j]=max(f[i][j],f[i−1][j−v[i]]+w[i])
f
[
i
−
1
]
[
j
−
v
[
i
]
]
+
w
[
i
]
f[i - 1][j - v[i]] + w[i]
f[i−1][j−v[i]]+w[i]是上一行的状态,若从前往后更新,上一行的状态将被覆盖,所以从后往前更新
多重背包
使用次数有限,每个物品有
s
i
s_i
si个,也就是最多使用
s
i
s_i
si次
朴素解法与完全背包一样,只是需要添加限制:每个物品的选择次数不能超过
s
i
s_i
si
for (int i = 1; i <= n; ++ i )
for (int j = 1; j <= m; ++ j )
for (int k = 0; k <= s[i] && k * v[i] <= j; ++ k )
f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);
printf("%d\n", f[n][m]);
正常情况下,该解法将超时,那么如何优化朴素解法?
多重背包的状态表示和之前的背包问题一样,只有状态计算不一样
f
(
i
,
j
)
=
m
a
x
(
f
(
i
−
1
,
j
)
,
f
(
i
−
1
,
j
−
v
i
)
+
w
i
,
f
(
i
−
1
,
j
−
2
∗
v
i
)
+
2
∗
w
i
,
.
.
.
)
f(i, j) = max(f(i-1, j), f(i-1, j-v_i)+w_i, f(i-1, j-2*v_i)+2*w_i, ...)
f(i,j)=max(f(i−1,j),f(i−1,j−vi)+wi,f(i−1,j−2∗vi)+2∗wi,...)
可以表示成
f
(
i
,
j
)
=
m
a
x
(
f
(
i
−
1
,
j
−
k
∗
v
[
i
]
)
+
k
∗
w
[
i
]
)
f(i, j) = max(f(i-1, j-k*v[i]) + k*w[i])
f(i,j)=max(f(i−1,j−k∗v[i])+k∗w[i]),其中k从0到
s
i
s_i
si
式子的形式和完全背包很像,可以用完全背包的优化方法优化多重背包吗?
考虑状态两个状态
f
(
i
,
j
)
f(i, j)
f(i,j)与
f
(
i
,
j
−
v
i
)
f(i, j-v_i)
f(i,j−vi)

与完全背包不同,多重背包的
f
(
i
,
j
−
v
i
)
f(i, j-v_i)
f(i,j−vi)比
f
(
i
,
j
)
f(i, j)
f(i,j)的最后多出了一项,由于这一项的存在,
f
(
i
,
j
−
v
i
)
f(i, j-v_i)
f(i,j−vi)就推导不出
f
(
i
,
j
)
f(i, j)
f(i,j)。
为什么完全背包的
f
(
i
,
j
−
v
i
)
f(i, j-v_i)
f(i,j−vi)的最后不会多出一项?
区别就在于完全背包可以选择无限次,直到背包能装下k个物品,却装不下(k+1)个物品,此时k最大,背包能装最多的第i个物品
完全背包的
f
(
i
,
j
)
f(i, j)
f(i,j)和
f
(
i
,
j
−
v
i
)
f(i, j-v_i)
f(i,j−vi)中,两者最后一项的k都是最大的,即
f
(
i
−
1
,
j
−
k
∗
v
i
)
f(i-1, j-k*v_i)
f(i−1,j−k∗vi)中,
j
−
k
∗
v
i
>
0
j-k*v_i>0
j−k∗vi>0,
j
−
(
k
+
1
)
∗
v
i
<
0
j-(k+1)*v_i<0
j−(k+1)∗vi<0
多重背包的
f
(
i
,
j
)
f(i, j)
f(i,j)的最后一项为
f
(
i
−
1
,
j
−
k
∗
v
i
)
+
k
∗
w
i
f(i-1, j-k*v_i) + k*w_i
f(i−1,j−k∗vi)+k∗wi,其中
j
−
k
∗
v
i
>
0
j-k*v_i>0
j−k∗vi>0,
k
=
s
i
k=s_i
k=si,等于题目限制的最多选择第i个物品的数量
- 若 j − ( k + 1 ) ∗ v i > 0 j-(k+1)*v_i>0 j−(k+1)∗vi>0,那么 f ( i , j − v i ) f(i, j-v_i) f(i,j−vi)的最后一项为 f ( i − 1 , j − ( k + 1 ) ∗ v i ) + k ∗ w i f(i-1, j-(k+1)*v_i) + k*w_i f(i−1,j−(k+1)∗vi)+k∗wi,此时无法推导 f ( i , j ) f(i, j) f(i,j)
- 若 j − ( k + 1 ) ∗ v i < 0 j-(k+1)*v_i<0 j−(k+1)∗vi<0,那么 f ( i , j − v i ) f(i, j-v_i) f(i,j−vi)的最后一项为 f ( i − 1 , j − k ∗ v i ) + ( k − 1 ) ∗ w i f(i-1, j-k*v_i) + (k-1)*w_i f(i−1,j−k∗vi)+(k−1)∗wi,此时可以推导 f ( i , j ) f(i, j) f(i,j)
所以多重背包与完全背包的优化不同, f ( i , j − v i ) f(i, j-v_i) f(i,j−vi)无法推导 f ( i , j − v ) f(i, j-v) f(i,j−v)的原因是:k最大时,多重背包的 k ∗ v i k*v_i k∗vi可能临界背包的容量,而完全背包的 k ∗ v i k*v_i k∗vi一定临界背包的容量,此时 f ( i , j − v i ) f(i, j-v_i) f(i,j−vi)的最后一项不存在,因为背包无法装下
多重背包采用二进制优化:
优化之前,对于每个物品,我们需要试着将
s
i
s_i
si个物品装入背包,以更新能选择的最大价值
这是一个线性的计算,完全背包能将这个线性的计算优化成常数级别的计算,多重背包能将其优化成O(logn) 级别的计算
将物品分组,每组的物品数量为
2
i
2^i
2i,同时每组的物品数量各不相同,并且只能被选择一次
假设能选择
s
i
s_i
si个第i个物品,将
s
i
s_i
si进行分组:
2
0
,
2
1
,
2
2
,
.
.
.
,
2
l
o
g
s
i
2^0, 2^1, 2^2, ... , 2^{logs_i}
20,21,22,...,2logsi,选择其中的任意组进行相加,就能得到(0~
s
i
s_i
si)中的任何数
假设每组背包的数量为
2
0
,
2
1
,
2
2
2^0, 2^1, 2^2
20,21,22,在每组背包只选择一次的情况下,选择其中的任意组进行相加,得到的物品数量为(1~7)。即
2
0
,
2
1
,
2
2
2^0, 2^1, 2^2
20,21,22能构成1~7中任意一个数,比如
5
=
2
0
+
2
2
,
7
=
2
0
+
2
1
+
2
2
5=2^0+2^2, 7=2^0+2^1+2^2
5=20+22,7=20+21+22
此时多重背包问题就被转化成了01背包问题
一个线性的复杂度O(n) 就被优化成了O(logn)
假设
s
i
=
200
s_i=200
si=200,此时如何分组?先从最小的开始:
2
0
,
2
1
,
2
2
,
2
3
,
2
4
,
2
5
,
2
6
2^0, 2^1, 2^2, 2^3, 2^4, 2^5, 2^6
20,21,22,23,24,25,26,此时选择任意组进行相加,得到的物品数量为(0127),$127=2^7-1$。不能再分一组数量为$2^7$的背包,因为数量不够,只剩下73个物品。此时将剩下的物品为一组,已知之前的分组能组成的背包数量为(0127),(0127)中的任意数量与73相加能得到(73200),合并一下
那么
2
0
,
2
1
,
2
2
,
2
3
,
2
4
,
2
5
,
2
6
,
73
2^0, 2^1, 2^2, 2^3, 2^4, 2^5, 2^6, 73
20,21,22,23,24,25,26,73,选择任意组进行相加,得到的物品数量为(0~200)
推广一下,先将
s
i
s_i
si分成
2
0
,
2
1
,
2
2
,
.
.
.
,
2
k
2^0, 2^1, 2^2, ... , 2^k
20,21,22,...,2k,此时能组成(0~
2
k
+
1
−
1
2^{k+1}-1
2k+1−1)之间的任何数
若
2
k
+
1
−
1
<
s
i
<
2
k
+
2
−
1
2^{k+1}-1 < s_i < 2^{k+2}-1
2k+1−1<si<2k+2−1,说明
s
i
−
(
2
k
+
1
−
1
)
<
2
k
+
1
s_i-(2^{k+1}-1) < 2^{k+1}
si−(2k+1−1)<2k+1,用c表示:
c
<
2
k
+
1
c < 2^{k+1}
c<2k+1
此时我们要将c分为一组,使得
c
+
(
2
k
+
1
−
1
)
=
s
i
c+(2^{k+1}-1) = s_i
c+(2k+1−1)=si
由于之前的分组能组成(0$2^{k+1}-1$)之间的所有数,这些数中的任意数与数量为c的分组相加后,能组成(c
2
k
+
1
−
1
+
c
2^{k+1}-1+c
2k+1−1+c)中的所有数,也就是(c~
s
i
s_i
si)之间的所有数
由于
c
<
2
k
+
1
c<2^{k+1}
c<2k+1,所以可以将(0$2^{k+1}-1$)与(c
s
i
s_i
si)合并,最终
2
0
,
2
1
,
2
2
,
.
.
.
,
2
k
,
c
2^0, 2^1, 2^2, ... , 2^k, c
20,21,22,...,2k,c能组成(0~
s
i
s_i
si)之间的所有数
对
s
i
s_i
si进行二进制优化后,将优化后的问题看成01背包问题即可
模板就是01背包的模板,不同的是:用来动规的体积数组以及价值数组是预处理后的
如何预处理?根据
s
i
s_i
si不断地划分出
2
i
2^i
2i,将每个物品的体积与容量乘以
2
i
2^i
2i
for (int i = 1; i <= n; ++ i ) // n为物品的数量
{
scanf("%d%d%d", &pv, &pw, &s); // 读取该物品的体积,容积以及能选择的次数
int k = 1;
while (k <= s)
{
v[cnt] = k * pv;
w[cnt] = k * pw;
s -= k;
k *= 2; // 注意这两个式子的先后顺序
cnt ++ ;
}
if (s > 0)
{
v[cnt] = s * pv;
w[cnt] = s * pw;
cnt ++ ;
}
}
分组背包
给定v组物品以及其中每个物品的价值与体积,每组物品只能选择一个物品,问如何选择装入最大价值?
状态表示:从前i组中选,体积不超过j的所有选法,属性为价值的最大值
状态计算:
f
(
i
,
j
)
f(i, j)
f(i,j)可以划分成两个集合,一个集合选择第i组物品中的某一个,一个集合不选择第i组物品,两个集合不重不漏组成
f
(
i
,
j
)
f(i, j)
f(i,j)
不选择第i组物品的状态为
f
(
i
−
1
,
j
)
f(i-1, j)
f(i−1,j)
选择第i组物品的状态为
f
(
i
−
1
,
j
−
v
[
i
,
k
]
)
f(i-1, j-v[i,k])
f(i−1,j−v[i,k]),其中k表示第i组物品中第k个物品,假设第i组有n个物品,那么k从1~n
合并两个状态,k就是从0~n
for (int i = 1; i <= n; ++ i )
{
for (int j = 1; j <= m; ++ j )
{
f[i][j] = f[i - 1][j];
for (int k = 1; k <= s[i]; ++ k )
{
if (v[i][k] <= j) f[i][j] = max(f[i][j], f[i - 1][j - v[i][k]] + w[i][k]);
}
}
}
printf("%d\n", f[n][m]);
若k从1~n,那么f[i][j] = f[i - 1][j];不能写到k循环中,若要写到k循环中,要取max:f[i][j] = max(f[i][j], f[i - 1][j]);,因为选择第i组的物品后,f[i][j]可能大于f[i-1][j]。之前的背包问题省略了max是因为是否取max不影响最后的结果
可以写成这样:
for (int i = 1; i <= n; ++ i )
{
for (int j = 1; j <= m; ++ j )
{
for (int k = 1; k <= s[i]; ++ k )
{
f[i][j] = max(f[i][j], f[i - 1][j]);
if (v[i][k] <= j) f[i][j] = max(f[i][j], f[i - 1][j - v[i][k]] + w[i][k]);
}
}
}
printf("%d\n", f[n][m]);
也可以将k从0~n
for (int i = 1; i <= n; ++ i )
{
for (int j = 1; j <= m; ++ j )
{
for (int k = 0; k <= s[i]; ++ k )
{
if (v[i][k] <= j) f[i][j] = max(f[i][j], f[i - 1][j - v[i][k]] + w[i][k]);
}
}
}
printf("%d\n", f[n][m]);
然后直接压缩状态
for (int i = 1; i <= n; ++ i )
for (int j = m; j >= 1; -- j )
for (int k = 0; k <= s[i]; ++ k )
if (v[i][k] <= j) f[j] = max(f[j], f[j - v[i][k]] + w[i][k]);
printf("%d\n", f[m]);
注意j从后往前的更新
背包练习题
2. 01背包问题
2. 01背包问题 - AcWing题库
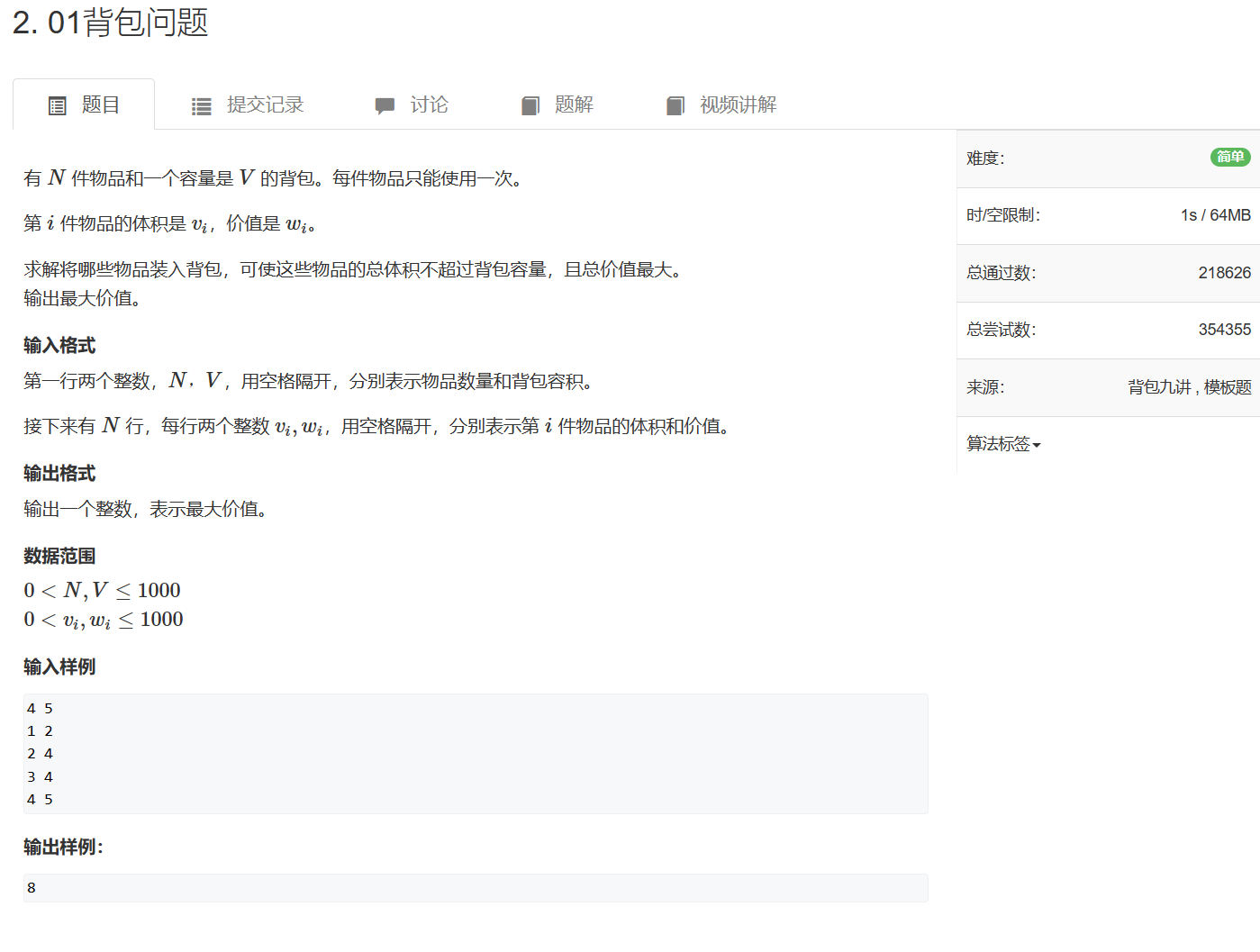
#include <iostream>
using namespace std;
const int N = 1010;
int v[N], w[N]; // 体积与价值
int f[N][N];
int main()
{
int n, m;
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; ++ i ) scanf("%d%d", &v[i], &w[i]);
for (int i = 1; i <= n; ++ i )
{
for (int j = 1; j <= m; ++ j )
{
f[i][j] = f[i - 1][j];
if (v[i] <= j) f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);
}
}
printf("%d\n", f[n][m]);
return 0;
}
滚动数组压缩
#include <iostream>
using namespace std;
const int N = 1010;
int v[N], w[N]; // 体积与价值
int f[N];
int main()
{
int n, m;
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; ++ i ) scanf("%d%d", &v[i], &w[i]);
for (int i = 1; i <= n; ++ i )
for (int j = m; j >= v[i]; -- j )
f[j] = max(f[j], f[j - v[i]] + w[i]);
printf("%d\n", f[m]);
return 0;
}
3. 完全背包问题
3. 完全背包问题 - AcWing题库
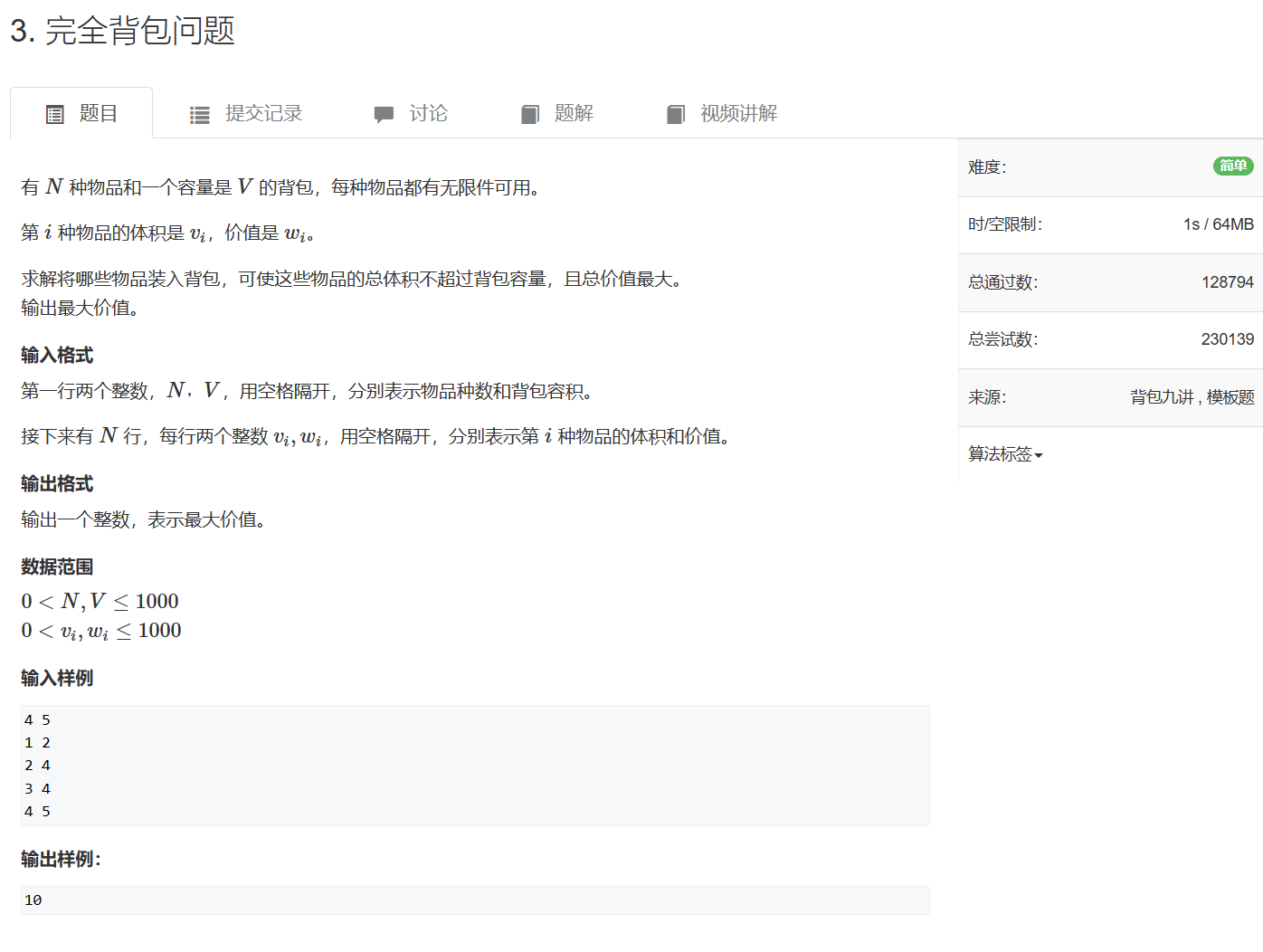
朴素解法,超时
#include <iostream>
using namespace std;
const int N = 1010;
int v[N], w[N];
int f[N][N];
int main()
{
int n, m;
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; ++ i ) scanf("%d%d", &v[i], &w[i]);
for (int i = 1; i <= n; ++ i )
{
for (int j = 1; j <= m; ++ j )
{
for (int k = 0; k * v[i] <= j; ++ k )
{
f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);
}
}
}
printf("%d\n", f[n][m]);
return 0;
}
需要压缩的二维dp
#include <iostream>
using namespace std;
const int N = 1010;
int v[N], w[N];
int f[N][N];
int main()
{
int n, m;
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; ++ i ) scanf("%d%d", &v[i], &w[i]);
for (int i = 1; i <= n; ++ i )
{
for (int j = 1; j <= m; ++ j )
{
f[i][j] = f[i - 1][j];
if (v[i] <= j) f[i][j] = max(f[i][j], f[i][j - v[i]] + w[i]);
}
}
printf("%d\n", f[n][m]);
return 0;
}
压缩后的一维dp
#include <iostream>
using namespace std;
const int N = 1010;
int v[N], w[N];
int f[N];
int main()
{
int n, m;
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; ++ i ) scanf("%d%d", &v[i], &w[i]);
for (int i = 1; i <= n; ++ i )
for (int j = v[i]; j <= m; ++ j )
f[j] = max(f[j], f[j - v[i]] + w[i]);
printf("%d\n", f[m]);
return 0;
}
4. 多重背包问题 I
4. 多重背包问题 I - AcWing题库
#include <iostream>
using namespace std;
const int N = 110;
int v[N], w[N], s[N];
int f[N][N];
int main()
{
int n, m;
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; ++ i) scanf("%d%d%d", &v[i], &w[i], &s[i]);
for (int i = 1; i <= n; ++ i )
for (int j = 1; j <= m; ++ j )
for (int k = 0; k <= s[i] && k * v[i] <= j; ++ k )
f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);
printf("%d\n", f[n][m]);
return 0;
}
5. 多重背包问题 II
5. 多重背包问题 II - AcWing题库
#include <iostream>
using namespace std;
const int N = 25000, M = 2010;
int v[N], w[N];
int f[M];
int main()
{
int n, m, cnt = 1;
scanf("%d%d", &n, &m);
int pv, pw, s;
for (int i = 1; i <= n; ++ i )
{
scanf("%d%d%d", &pv, &pw, &s);
int k = 1;
while (k <= s)
{
v[cnt] = k * pv;
w[cnt] = k * pw;
s -= k;
k *= 2; // 注意这两个式子的先后顺序
cnt ++ ;
}
if (s > 0)
{
v[cnt] = s * pv;
w[cnt] = s * pw;
cnt ++ ;
}
}
n = cnt - 1;
for (int i = 1; i <= n; ++ i )
for (int j = m; j >= v[i]; -- j )
f[j] = max(f[j], f[j - v[i]] + w[i]);
printf("%d\n", f[m]);
return 0;
}
9. 分组背包问题
9. 分组背包问题 - AcWing题库
#include <iostream>
using namespace std;
const int N = 110;
int v[N][N], w[N][N], s[N];
int f[N][N];
int main()
{
int n, m;
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; ++ i )
{
scanf("%d", &s[i]);
for (int j = 1; j <= s[i]; ++ j )
scanf("%d%d", &v[i][j], &w[i][j]);
}
for (int i = 1; i <= n; ++ i )
{
for (int j = 1; j <= m; ++ j )
{
f[i][j] = f[i - 1][j];
for (int k = 1; k <= s[i]; ++ k )
{
if (v[i][k] <= j) f[i][j] = max(f[i][j], f[i - 1][j - v[i][k]] + w[i][k]);
}
}
}
printf("%d\n", f[n][m]);
return 0;
}
压缩状态后:
#include <iostream>
using namespace std;
const int N = 110;
int v[N][N], w[N][N], s[N];
int f[N];
int main()
{
int n, m;
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; ++ i )
{
scanf("%d", &s[i]);
for (int j = 1; j <= s[i]; ++ j )
scanf("%d%d", &v[i][j], &w[i][j]);
}
for (int i = 1; i <= n; ++ i )
{
for (int j = m; j >= 1; -- j )
{
for (int k = 0; k <= s[i]; ++ k )
{
if (v[i][k] <= j) f[j] = max(f[j], f[j - v[i][k]] + w[i][k]);
}
}
}
printf("%d\n", f[m]);
return 0;
}