【HDU No. 2243】单词情结 考研路茫茫——单词情结

杭电OJ 题目地址

【题意】

单词和词根仅由小写字母组成。给定N个词根，求长度不超过L 且至少包含一个词根的单词可能有多少个？

若有两个词根aa和ab，则长度不超过3且至少包含一个词根的单词可能存在104个：aa, ab（两个）、aaa, aab, aac…aaz（26个）、aba, abb,abc…abz（26个）、baa, caa, daa…zaa（25个）、bab, cab, dab…zab（25个）。

【输入输出】

输入：

包含多个测试用例。每个测试用例都占两行。第1行有两个正整数N 和L （0<N <6，0<L <231 ）。第2行有N 个词根，每个词根的长度都不超过5。

输出：

对每个测试用例，都单行输出满足条件的单词总数mod 264的值。

【样例】

【思路分析】

本题求解长度不超过L 且至少包含一个词根的单词可能共计多少个。

这道题和 POJ2778有两处不同。

• 本题中长度不超过L ；POJ2778中长度为n。
• 本题求解的是至少包含一个词根的单词数，POJ2778求解的是不包含遗传病片段的DNA序列数。

【算法设计】

① 求解由26个小写字母组成且长度不超过L 的单词数ans。

② 求解长度不超过L 且不包含词根的单词数res。

③ 长度不超过L 且至少包含一个词根的单词数为两者之差ansres。

【举个栗子】

① 长度不超过L 的单词数

长度不超过L 的单词包括长度为1的26个、长度为2的26^2 个……长度为L 的26^ L 个，其和值26+26^2 +…+26^L 为长度不超过L 的单词数，如何计算呢？

对等比矩阵求和有经典算法，假定原矩阵为 A ，阶数为n ，则构造一个阶数为2n 的矩阵，其中0代表0矩阵， E 代表单位矩阵：

|A E|
|0 E|

求出的K 次矩阵的右上n 子矩阵正好是等比矩阵的K 项和。

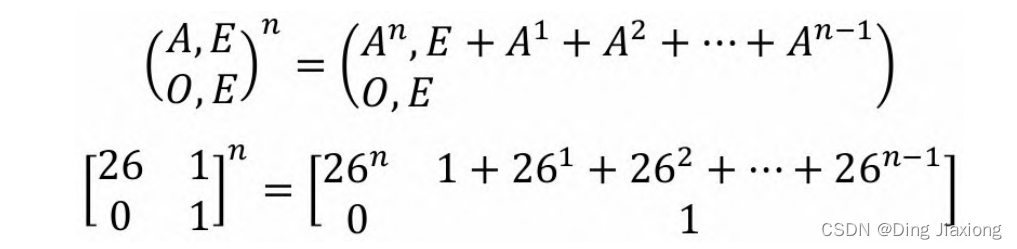
求出矩阵的n 次幂的第1行之和减1，即可得到ans=26^1 +26^2 +…+26^(n -1) +26^n ，因为mod 2^64 ，所以直接用unsigned long long就可以了，系统会自动截断，相当于取模运算。

② 长度不超过L 且不包含词根的单词数

现在求解不超过L 且不包含词根的单词数，需要将所有长度小于或等于L 且不包含词根的单词数累加。要实现累加结果，只需在矩阵最后一行添加0，在最后一列添加1即可。

根据输入样例1的词根{aa ab}构建AC自动机，如下图所示。

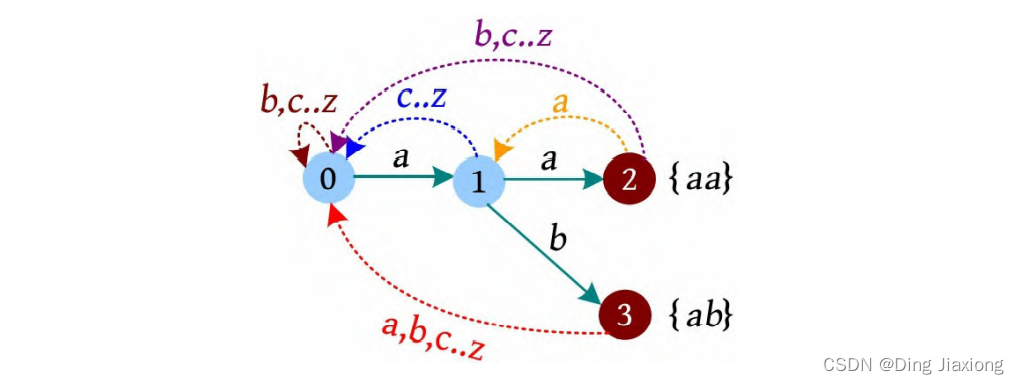
不包含词根的原矩阵如下：

25 1
24 0

为实现累加效果，在原矩阵的最后一行添加0且在最后一列添加1，单位矩阵变为：

25 1 1
24 0 1
0  0 1

若M [i , j ]表示从节点i 到j 只走1步有几种走法，则 M 的n 次幂表示从节点i 到j 走n 步有几种走法。求出矩阵的n 次幂第1行之和减1，得到长度不超过L 且不包含词根的单词数res。

③ 长度不超过L 且至少包含一个词根的单词数

长度不超过L 且至少包含一个词根的单词数为两者之差ans-res。

【算法实现】

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<queue>

using namespace std;

typedef unsigned long long ll;

const int maxn=40;
const int K=26;
int root,L;

struct mat{
	ll a[maxn][maxn];
	int n;
	mat(int _n){
		n=_n;
		memset(a,0,sizeof(a));
	}
};

mat mul(mat A,mat B){//矩阵乘法
    mat C(A.n);
    for(int i=0;i<A.n;i++)
        for(int j=0;j<B.n;j++)
            for(int k=0;k<A.n;k++)
                C.a[i][j]+=A.a[i][k]*B.a[k][j];
    return C;
}

mat pow(mat A,int n){//A^n
    mat ans(A.n);
    for(int i=0;i<A.n;i++)
        ans.a[i][i]=1;//单位矩阵 
    while(n>0){
        if(n&1)
			ans=mul(ans,A);
        A=mul(A,A);
        n>>=1;
    }
    return ans;
}

struct ACAutomata{
    int next[maxn][K],fail[maxn],end[maxn],id[maxn];
    int newNode(){//新建结点
        for(int i=0;i<K;i++)
			next[L][i]=-1;
        end[L]=0;
        return L++;
    }
    void init(){//初始化
        L=0;
        root=newNode();
    }
    void insert(char s[]){//插入一个结点
        int len=strlen(s);
        int p=root;
        for (int i=0;i<len;i++){
            int ch=s[i]-'a';
            if(next[p][ch]==-1)
				next[p][ch]=newNode();
            p=next[p][ch];
        }
        end[p]++;
    }
    void build(){//构建AC自动机
        queue<int> Q;
        fail[root]=root;
        for (int i=0;i<K;i++){
            if(next[root][i]==-1){
                next[root][i]=root;
            }
			else{
                fail[next[root][i]]=root;
                Q.push(next[root][i]);
            }
        }
        while(Q.size()){
            int now=Q.front();
            Q.pop();
            if(end[fail[now]])
				end[now]++;//重要!!如果当前结点的失败指针end有结束标记，当前结点的end++ 
            for(int i=0;i<K;i++){
                if (next[now][i]!=-1){
                    fail[next[now][i]]=next[fail[now]][i];
                    Q.push(next[now][i]);
                }
				else
					next[now][i]=next[fail[now]][i];
            }
        }
    }

    ll query(int n){
        int ids=0;
        memset(id,-1,sizeof(id));
        for(int i=0;i<L;i++)//对未标记的结点重新编号 
        	if(!end[i])
        		id[i]=ids++;
        mat F(ids+1);		
        for(int u=0;u<L;u++){
        	if(end[u]) continue;
        	for(int j=0;j<K;j++){
                int v=next[u][j];
                if(!end[v])
					F.a[id[u]][id[v]]++;
            }
		}
		for(int i=0;i<ids+1;i++)
			F.a[i][ids]=1;

	    F=pow(F,n);

	    ll res=0;
	    for(int i=0;i<L;i++)
	    	res+=F.a[0][i];
	    return --res;
    }
}ac;

ll pow_2(int n){//求26+26^2+...+26^n
	mat C(2);
    C.a[0][0]=26;
    C.a[0][1]=C.a[1][1]=1;
    C=pow(C,n);
    ll ans=C.a[0][0]+C.a[0][1];
    return --ans;
}

int main(){
	
    int m,n;
    char str[20];
    while(~scanf("%d%d",&m,&n)){
        ac.init();
        while (m--){
            scanf("%s",str);
            ac.insert(str);
        }
        ac.build();
        cout<<pow_2(n)-ac.query(n)<<endl;
    }
	
    return 0;
}