[论文阅读] 颜色迁移-梯度保护颜色迁移

文章: [Gradient-Preserving Color Transfer], [代码未公开]

本文目的: 如题所示为梯度保护的颜色迁移方法.

1-算法原理

人类的视觉系统对局部强度差异比强度本身更敏感, 因而, 保持颜色梯度是场景保真度的必要条件, 因而作者认为: 一个好的颜色迁移算法需要保持颜色梯度.

颜色梯度从字面意思理解就是要保持颜色和梯度, 颜色迁移就是要保持源图像中的细节(梯度)和目标图像中的颜色.

因而本文就是从2这个方面进行设计算法的, 最小化如下所示公式, 即可得到输出图像.

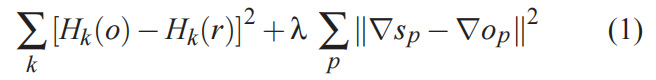
式中, $H(\ast )$ 为直方图, $\nabla$ 为梯度算子

• 第一部分是直方图, 用于获取目标/参考图像颜色, 输出图像的直方图和目标/参考图像的直方图尽可能的接近
• 第二部分是梯度, 用于保留源图像梯度, 输出图像的梯度和源图像的梯度尽可能的接近
• 参数λ是用于平衡目标图像颜色和源图像梯度的系数

但上述公式1很难优化, 主要原因函数 $H(\ast )$ 是作用于图像整体的统计运算, 而梯度算子 $\nabla$ 是应用于图像中的每个像素.

1.1-方法简化

针对公式难以优化问题, 作者对公式进行了简化:

• 公式1的第一部分作用是尽可能的使输出图像的直方图接近目标图像的直方图, 其功能就相当于直方图匹配
• 可以先将源图像和目标图像进行直方图匹配, 得到中间图像f
• 输出图像尽可能的接近中间图像f, 相当于输出图像直方图尽可能接近目标图像直方图

因而上述公式可以更改为:

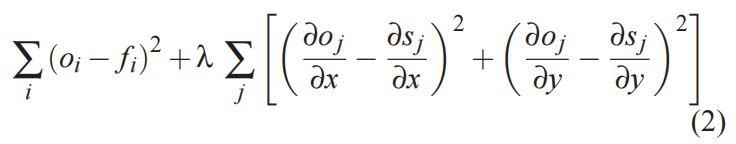
进一步地, 使用矩阵方式表示, 并求导可以得到:

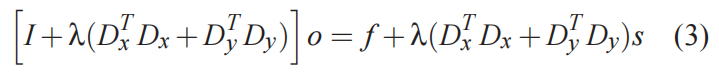
式中, $o$ 输出的图像, $D_x$ , $D_y$ 为梯度算子, 文中使用sobel算子, 关于sobel算子, 可以戳这里: Sobel算子

2-算法核心

2.1-关于公式简化

比较难以理解的是公式2到公式3的变换, 这里做个简单说明, 可能不太正确.

要求公式2的最小值, 就要求其导数=0时的解, 为了方便理解, 这里去除下标, 对单个像素进行说明, 对公式2求导:

$$\begin{gathered} 2(o-f)+\lambda [2(D_x\ast o-Dx\ast s)\ast Dx+2(D_y\ast o-Dy\ast s)\ast Dy]=0 \\ o+\lambda (D_x^2\ast o+D_y^2\ast o)=f+\lambda (D_x^2\ast s+D_y^2\ast s) \\ [1+\lambda (D_x^2+D_y^2)]o=f+\lambda (D_x^2+D_y^2)s \end{gathered}$$

当对于所有像素, 使用矩阵表示时, $D_x^2$ 为 $D_x^T{D}_x$, 这样就可以得到公式3.

这样就可以通过求解线性方程得到输出图像o:

$$\begin{gathered} o=A^{-1}b \\ A=I+\lambda (D_x^T{D}_x+D_y^T{D}_y) \\ b=f+\lambda (D_x^T{D}_x+D_y^T{D}_y)s \end{gathered}$$

2.2-关于参数λ

算法中的唯一控制参数为λ, 文中也进行了讨论.

文中使用了 MSE 来对颜色迁移后的图像进行定量评估, MSE 计算方式如下:

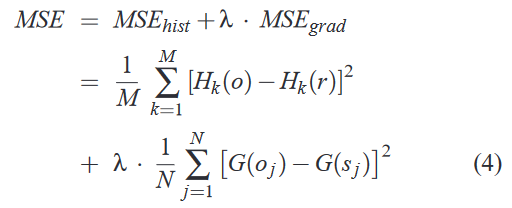
MSE的值随 λ 变化为变化, 经过文中例子进行测试, λ在1附近时, MSE的值最小(越小越好).

如下所示为不同λ时的结果对比.

3-算法复现

这里使用matlab对算法进行了复现, 结果如下所示:

RGB颜色空间

HSV颜色空间

Lab颜色空间

依次为源图像, 目标/参考图像, 结果.

4-参考

• Gradient-Preserving Color Transfer_铿锵的玫瑰的博客-CSDN博客