题目大意

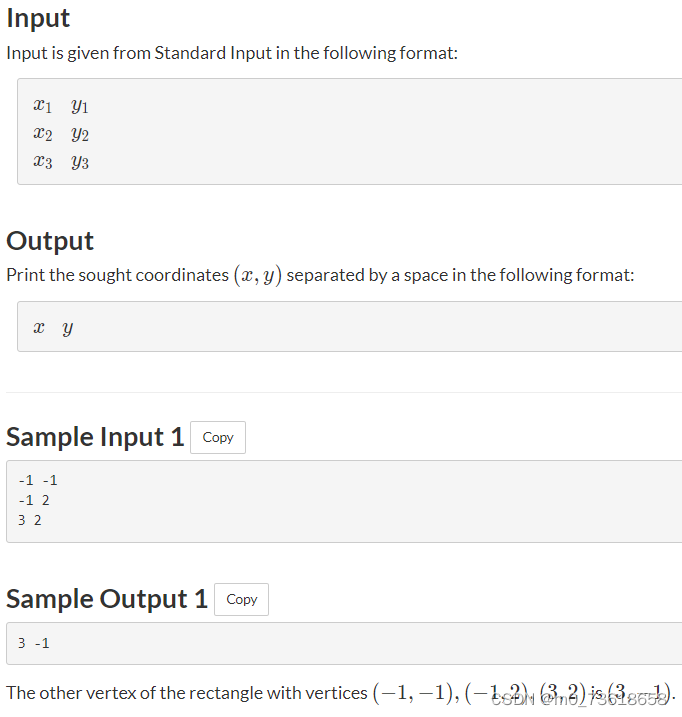
在平面上有一个矩形，矩形的每条边都平行于x轴或y轴，并且它的面积不为零。
给定这个矩形三个顶点的坐标 (x1, y1), (x2, y2), (x3, y3)，找到另外一个顶点的坐标。

思路分析

根据矩形的性质可以通过判断顶点的横坐标和纵坐标来确定另外一个顶点的坐标。

时间复杂度

O(1)

可AC代码

#include <iostream>
using namespace std;

int main(void)
{
  int x_1, x_2, x_3, y_1, y_2, y_3, x_ans, y_ans;
  
  cin >> x_1 >> y_1;
  cin >> x_2 >> y_2;  
  cin >> x_3 >> y_3;
  
  if(x_1 == x_2) x_ans = x_3;
  if(x_2 == x_3) x_ans = x_1;  
  if(x_3 == x_1) x_ans = x_2;  
  
  if(y_1 == y_2) y_ans = y_3;
  if(y_2 == y_3) y_ans = y_1;  
  if(y_3 == y_1) y_ans = y_2;
  
  cout << x_ans << " " << y_ans << endl;
  
  return 0;
}

B - Get CloserB - Get Closer

题目大意

要求在二维平面上从点(0,0)出发，向点(A,B)移动距离为1的距离，然后求移动后的坐标。

思路分析

首先可以根据两点之间的距离公式来求出距离d，其中d = sqrt(A^2 + B^2)。然后可以将坐标(A,B)除以d得到新的坐标(x,y)，即(x,y) = (A/d, B/d)。这样就得到了移动后的坐标

时间复杂度

O(1)

可AC代码

#include <iostream>
#include <cmath>

int main() {
    int A, B;
    std::cin >> A >> B;

    double d = std::sqrt(A * A + B * B);
    double x = A / d;
    double y = B / d;

    std::cout << x << " " << y << std::endl;

    return 0;
}

C - CouponC - Coupon

题目大意

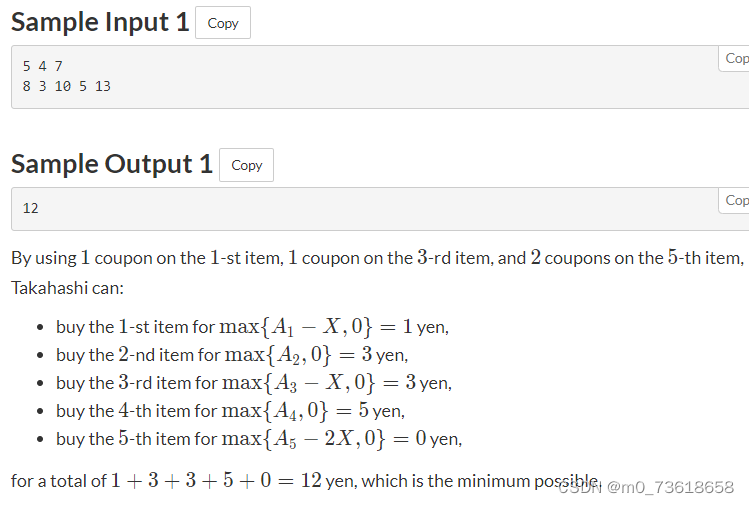
购物问题。有N个商品，在商店里出售。每个商品的价格分别为A1, A2, …, AN。Takahashi有K张优惠券，每张优惠券可以用于一件商品。对于每件商品，你可以使用任意数量的优惠券（包括零张）。使用k张优惠券在价格为a日元的商品上，可以以max(a - kX, 0)日元的价格购买它。现在需要计算Takahashi购买所有商品所需的最小金额。

思路分析

首先，可以使用尽可能多的类型1优惠券，即将优惠券应用于能够带来更大降价的商品上。具体操作如下：首先统计能够使用类型1优惠券的次数m，即对于每个商品，通过将商品价格除以X取整获得能够使用的优惠券数量，然后找到实际可用的优惠券数量m和K中的较小值。接着，将m个优惠券应用于商品，从总成本中减去m*X的金额。然后，对于仍未使用完的优惠券，将使用类型2优惠券，即选择当前价格最高的商品进行折扣。最后，将剩余的优惠券使用完或者商品遍历完后，输出最终的总成本。

知识点标签

数学运算
排序算法

时间复杂度

O(NlogN)

可AC代码

#include <iostream>
#include <algorithm>
using namespace std;
typedef long long ll;

ll n, k, x;
ll a[200005];

int main(void)
{
  
  cin >> n >> k >> x;
  for(int i = 1; i <= n; i++) cin >> a[i];
  // 初始化总成本为0
  ll ans = 0;
  // 计算总成本，即将所有商品的价格累加到ans中
  for(int i = 1; i <= n; i++) ans += a[i];

  // 定义变量m记录可用的类型1优惠券数量，初始化为0
  ll m = 0;
  
  // 根据题意，对于每个商品，通过将商品价格除以X取整获得能够使用的优惠券数量，并累加到m中
  for(int i = 1; i <= n; i++) m += a[i]/x;
  
  // 将实际可用的优惠券数量m和K中的较小值赋值给m
  m = min(m, k);
  
  // 从总成本中减去应用类型1优惠券后的金额，即减去m*X
  ans -= m*x;
  
  // 更新剩余可用的优惠券数量k
  k -= m;
  
  // 对于每个商品，计算其使用类型1优惠券后的价格
  for(int i = 1; i <= n; i++) a[i] %= x;
  
  // 对商品价格进行排序，以便后续应用类型2优惠券
  sort(a+1, a+n+1);
  
  // 从价格最高的商品开始，将剩余的优惠券应用于类型2优惠券，即选择当前价格最高的商品进行折扣
  for(int i = n; i >= 1; i--){
    if(k == 0) break;
    
    // 将当前商品的价格从总成本中减去
    ans -= a[i];
    
    // 更新剩余可用的优惠券数量k
    k--;
  }
  
  // 输出最终的总成本
  cout << ans << endl;
  
  return 0;
}