---

前言

平面坐标下判断三角形以及输出周长和面积, 用线性代数的简单知识.

---

一. 基本知识

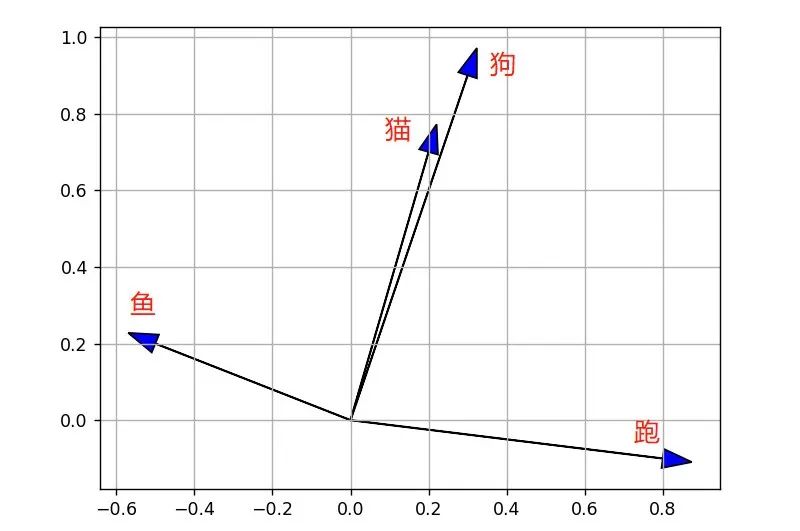
在平面坐标, 三个点就是三个向量, 可以通过两个向量同时减去第三个向量, 形成一个顶点在原点的三角形.

我们发现, 只有一种情况三角形不能成立, 就是从原点出发的两个向量在一条直线上

我们可以简单的用向量叉乘判断三角型是否成立, 同时, 向量叉乘的结果是向量形成的平行四边形面积

平行四边形面积的一半就是三角形面积

而三角型的周长, 可以根据勾股定理得出三条边的长度, 相加得出.

以下是代码:

#include <math.h>
#include <stdio.h>
 
// 定义向量结构体
typedef struct
{
    double x;
    double y;
} Vector;
 
// 计算向量的差
Vector sub(Vector vecA, Vector vecB)
{
    return (Vector){vecA.x - vecB.x, vecA.y - vecB.y};
}
 
// 计算向量的叉积
double cross(Vector vecA, Vector vecB)
{
    return vecA.x * vecB.y - vecA.y * vecB.x;
}
 
// 计算两点之间的距离
double distance(Vector pointA, Vector pointB)
{
    Vector subAB = sub(pointA, pointB);
    return sqrt(subAB.x * subAB.x + subAB.y * subAB.y);
}
 
// 计算三角形的周长
double triPer(Vector pointA, Vector pointB, Vector pointC)
{
    return distance(pointB, pointC) + distance(pointA, pointC) +
           distance(pointA, pointB);
}
 
// 返回三角形面积, 向量叉积的二分之一的绝对值
double triArea(Vector vecA, Vector vecB, Vector vecC)
{
    return fabs(cross(sub(vecB, vecA), sub(vecC, vecA))) / 2.0;
}
 
int main()
{
    Vector pointA;
    Vector pointB;
    Vector pointC;
 
    scanf("%lf %lf %lf %lf %lf %lf", &pointA.x, &pointA.y, &pointB.x, &pointB.y,
          &pointC.x, &pointC.y);
 
    double rest = triArea(pointA, pointB, pointC);
 
    // 判断平面三点是否可构成三角形, 即叉积不为零
    if (rest)
    {
        printf("L = %.2lf, A = %.2lf", triPer(pointA, pointB, pointC), rest);
    }
    else
    {
        printf("Impossible");
    }
 
    return 0;
}

---

总结

近期在学OpenGL, 顺便学点图形学, 顺便也就学点线性代数, 这就是另外一个世界了.