快速排序是一种基于分治思想的排序算法,它能够以极快的速度将一个乱序的数组重新排列成有序的序列。不仅如此,快速排序还具有简洁的实现代码和良好的可扩展性,成为最受欢迎的排序算法之一。接下来,让我带你了解一下它的魅力吧!💫
文章目录
- 快排基本思想:分而治之
- 双路快排(三种方法)
- hoare版本
- 常见误区
- 挖坑法版本
- 前后指针版本
- 三路划分版本
- 非递归版本
- 快速排序优化
- 1. 三数取中法选key
- 2. 递归到小的子区间时,可以考虑使用插入排序
- 快速排序的特性总结:
快排基本思想:分而治之
快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法.
快速排序的核心思想是“分而治之”。它将一个未排序的数组划分为两个子数组,然后对这两个子数组分别进行排序,最后再将排好序的子数组合并在一起。这个过程在递归的帮助下不断重复,直到整个数组有序为止。这种将问题切分成更小的子问题处理的方法,使得快速排序能够高效地处理大规模的数据。🌟
快速排序的核心操作是“划分”,通常是选择一个基准元素,将返回的基准位置分为左右两边,数组中比基准元素小的移到基准元素的左边,比基准元素大的移到基准元素的右边。这个过程称为“分区”,它保证了在完成一轮分区后,基准元素的位置是确定了的。接下来,基准元素的左右子数组将分别作为新的子问题继续递归处理。直到所有元素都排列在相应位置上为止。💥
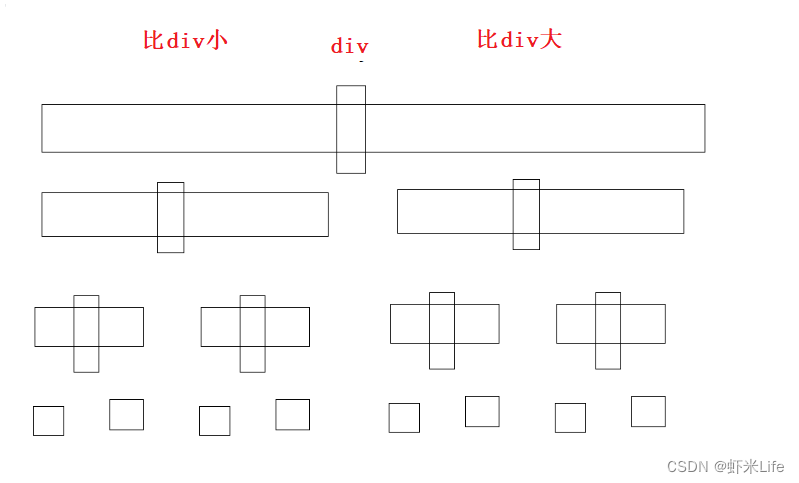
- div就在最终位置(排好序的位置)
- 左边有序,右边有序,整题就有序了
- 细节已写在代码注释上
// 假设按照升序对a 数组中[left, right]区间中的元素进行排序
void QuickSort(int* a, int left, int right)
{
//1、区间只有一个值
//2、区间不存在 就无需进行递归了
//递归的结束条件是子数组的长度小于等于1,此时子数组已经有序,不需要再进行排序。
if(left >= right )
return;
// 按照基准值对a数组的 [left, right]区间中的元素进行划分
int div = partSort(a, left, right);
// 返回的div已经确定了位置,无需在递归,只需要递归他的左右区间
// [begin, div-1] div [div+1, end]
// 划分成功后以div为边界形成了左右两部分 [left, div-1] 和 [div+1, right)
// 递归排[left, div-1]
QuickSort(a, left, div-1);
// 递归排[div+1, right]
QuickSort(a, div+1, right);
}
上述为快速排序递归实现的主框架,发现与二叉树前序遍历规则非常像,同学们在写递归框架时可想想二叉树前序遍历规则即可快速写出来,后序只需分析如何按照基准值来对区间中数据进行划分的方式即可。
- 将区间按照基准值划分为左右两半部分的常见方式有:
- 双路快排(三种方法)
1. hoare版本
2. 挖坑法版本
3. 前后指针版本 - 三路划分
- 双路快排(三种方法)
当然我们还会介绍我们的非递归方法完成快速排序.
以上的 非递归方法,双路快排,三路划分版本只需要学会两个即可 双路快排(任选之一方法),与非递归版本.
双路快排(三种方法)
hoare版本
Hoare版本的基本思想是::
选择序列的第一个元素作为基准值,并分别从序列的两端开始向中间遍历,交换不符合规则的元素,直到两个指针相遇。然后将基准值与指针相遇的位置的元素交换,此时基准值左侧的元素都小于等于它,右侧的元素都大于等于它。再对左右两个子序列分别递归进行同样的操作,直到排序完成。
单趟排序:
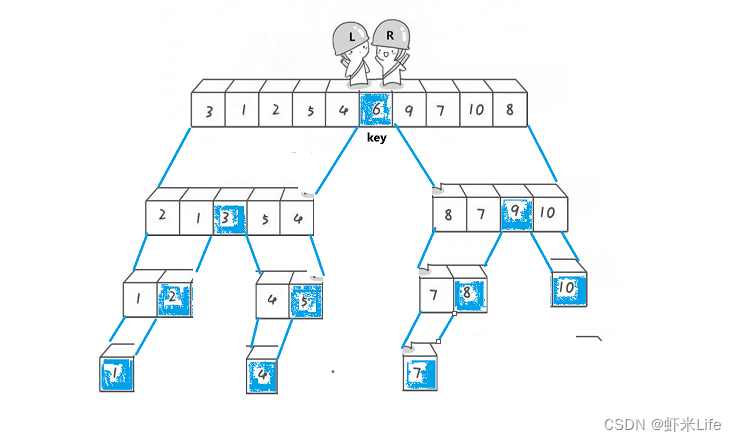
首先我们要确定第一个元素为基准值,命名为key.先从右边指针移动,查找比基准值(key)要少的值,在从左边指针开始移动,查找比基准值(key)要大的值,然后左右指针交换,直到两个指针相遇结束。将基准值与指针相遇的位置的元素交换. 此时基准值的左边元素都是比基准值小或者等于基准值,右边都比他大或者等于基准值。最后返回两个指针相遇位置下标

然后返回key,在递归他的左右区间,重复此过程,就完成整个排序了.蓝色标记的是基准值
- 代码实现
// Hoare版本
int Part_Sort1(int* a, int left, int right)
{
int midIndex = GetMidIndex(a, left, right); // 获取基准值的索引
swap(&a[left], &a[midIndex]); // 将基准值移到数组最左边
int keyi = left; // 基准值的索引
while (left < right)
{
// 右边找小于基准值的元素
while (left < right && a[right] >= a[keyi])//left < right防止越界
{
right--;
}
// 左边找大于基准值的元素
while (left < right && a[left] <= a[keyi])//left < right防止越界
{
left++;
}
swap(&a[left], &a[right]); // 交换左右两边的元素
}
swap(&a[keyi], &a[right]); // 将基准值放到正确的位置上
return right; // 返回基准值的索引
}
void QuickSort(int* a, int left, int right)
{
if(left >= right )
return;
// 按照基准值对a数组的 [left, right]区间中的元素进行划分
int div = part_Sort1(a, left, right);
// 返回的div已经确定了位置,无需在递归,只需要递归他的左右区间
// [begin, div-1] div [div+1, end]
// 划分成功后以div为边界形成了左右两部分 [left, div-1] 和 [div+1, right)
// 递归排[left, div-1]
QuickSort(a, left, div-1);
// 递归排[div+1, right]
QuickSort(a, div+1, right);
}
常见误区
-
常见误区1: 为什么中间两个while循环中判断条件是
a[right] >= a[keyi]和a[left] <= a[keyi]还要继续做++ 和 – 的操作尼?
其实很好理解,举个案例就完全清晰了.
假如是a[right] > a[keyi]和a[left] < a[keyi]
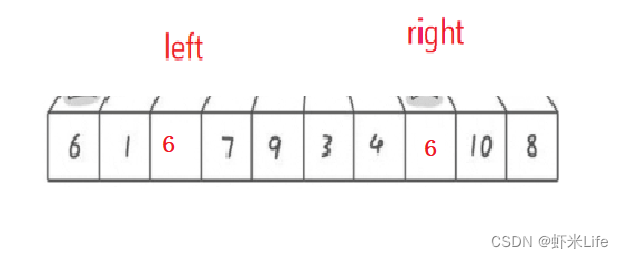
假设 left 和 right 都达到了和key相同元素位置,就会造成一直交换,a[right] > a[keyi]和a[left] < a[keyi]没有机会进入循环做++和- -操作.最后造成死循环. -
常见误区2: 为什么left的起始位置不是在keyi的后面,即keyi+1.
如果是写成left = keyi + 1是起始位置那这样对吗.
跟上面一样举个案例就完全清晰了.
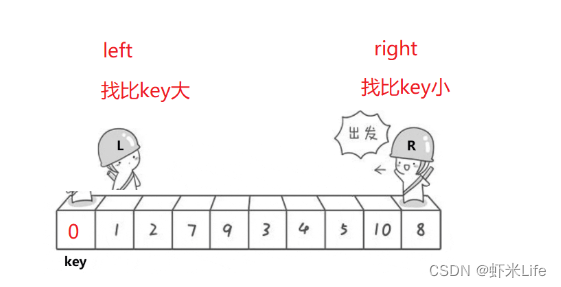
此时left是从key+1出发的,right一路向左移动找比key小的,直到遇见了left.最后循环结束,将基准值与指针相遇的位置的元素交换.
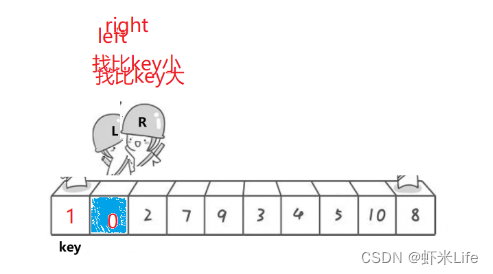
如图所示,right 和 left 在 keyi+1 的位置相遇,可能导致错误的交换。因此,要避免这个问题,确保 left 不从 keyi+1 开始。 -
常见误区3: 能不能先从右边指针开始移动。
直接说结果: 如果是从左边做基准值是不行的,大家可以拿这个例子试试{6,1,2,7,9,3,4,5,10,8}模拟一下过程.
结论:- 左边做key,右边先走; 保障了相遇位置的值比key小
- 右边做key,左边先走; 保障了相遇位置的值比key大
- 我们说下这一种情况:左边做key,右边先走; 保障了相遇位置的值比key小 or 就是key
L和R相遇无非就是两种情况,L遇R和R遇l-
情况一: L遇R,R是停下来,L在走,R先走,R停下来的位置一定比key小相遇的位置就是R停下的位置,就一定比key要小.
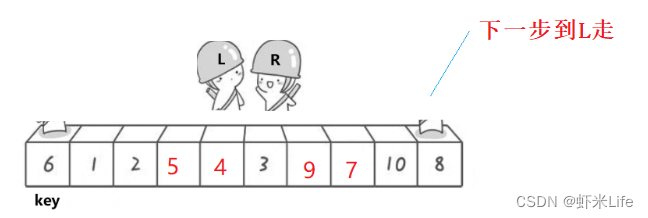
-
情况二: R遇L,在相遇这一轮,L就没动,R在移动,跟L相遇,相遇位置就是L的位置,L的位置就是key的位置 or 交换过一些轮次,相遇L位置一定比key小
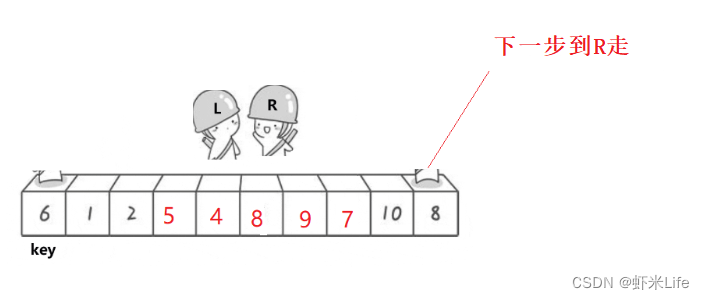
其实大家举个反例推理一下思路会更加清晰,一目了然了.
-
挖坑法版本
挖坑法版本相比hoare版本更加好理解,坑也没有hoare版本那么多,虽然他叫挖坑法哈哈.但是他会自己填坑.其思路其实是差不多的.
基本思想:
- 选择基准元素(通常是数组的第一个元素)。坑一开始的位置 (通常也是数组第一个元素下标的位置) 。
- 从数组的
右端开始移动,找到一个比基准元素小的元素,将其填入所在的坑位置,然后自己形成一个新坑。 - 在从数组的
左端开始移动,找到一个比基准元素大的元素,将其填入上一步形成的坑中。然后自己在形成一个新的坑。 - 重复步骤2和步骤3,直到左右指针相遇。
- 循环结束后将
基准元素放置到最后一个坑中。 - 返回最后一个坑位置下标
单趟排序:

- 为了更仔细的观看,我自己手动模拟一下,
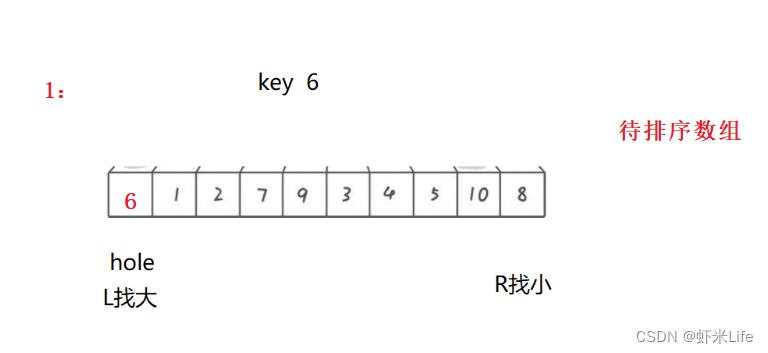
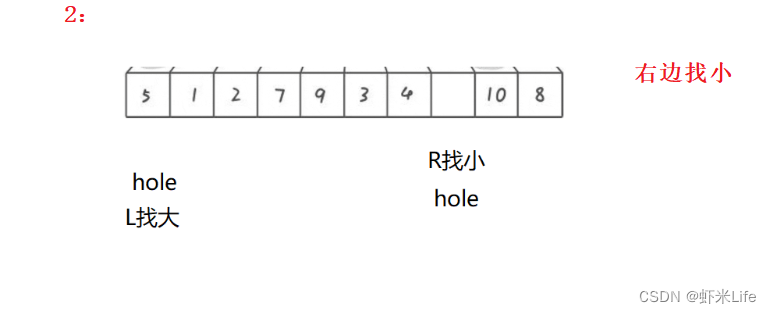
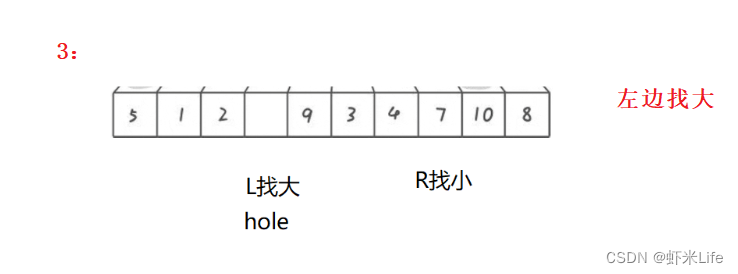
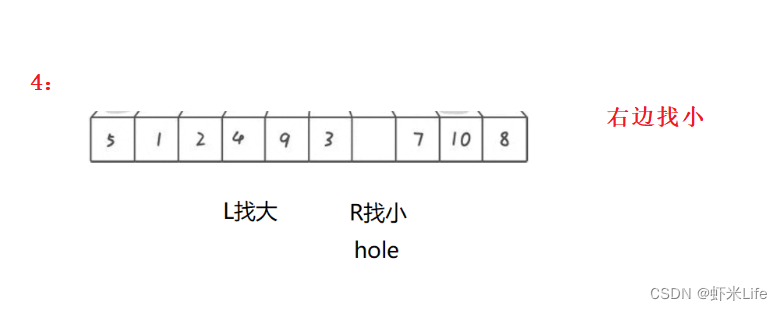
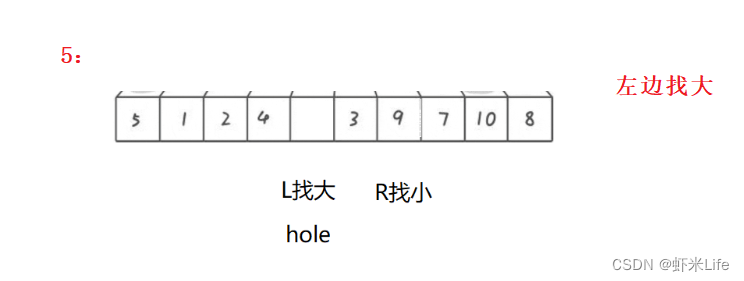
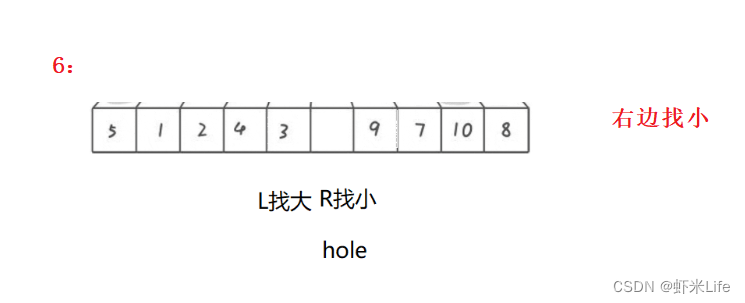
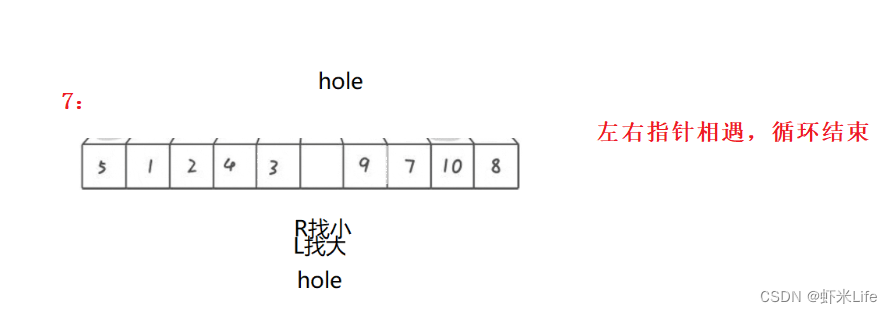
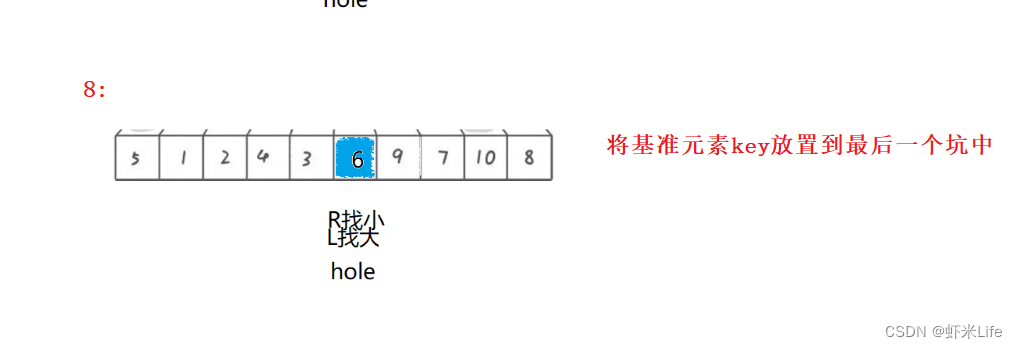
通过这种方式,每一趟排序都会将一个基准元素放置到正确的位置上,并形成一个新的坑,然后再对左右两部分进行排序。这样不断重复,直到整个数组有序。挖坑法的关键在于通过交替填坑的方式实现元素的分割和排序。
每一趟的递归我就不写了这里,大家可以看看hoare版本那个图,只是单趟处理数据的方式不一样.
- 代码实现
// 挖坑法
int Part_Sort2(int* a, int left, int right)
{
int midIndex = GetMidIndex(a, left, right); // 获取基准值的索引
swap(&a[left], &a[midIndex]); // 将基准值移到数组最左边
int key = a[left]; // 基准值
int tmp = left; // 坑的位置
while (left < right)
{
// 右边找小于基准值的元素
while (left < right && a[right] >= key)
{
right--;
}
a[tmp] = a[right]; // 将找到的元素放入坑中
tmp = right;
// 左边找大于基准值的元素
while (left < right && a[left] <= key)
{
left++;
}
a[tmp] = a[left]; // 将找到的元素放入坑中
tmp = left;
}
a[tmp] = key; // 将基准值放入坑中
return tmp; // 返回基准值的索引
}
void QuickSort(int* a, int left, int right)
{
if(left >= right )
return;
// 按照基准值对a数组的 [left, right]区间中的元素进行划分
int div = part_Sort2(a, left, right);
// 返回的div已经确定了位置,无需在递归,只需要递归他的左右区间
// [begin, div-1] div [div+1, end]
// 划分成功后以div为边界形成了左右两部分 [left, div-1] 和 [div+1, right)
// 递归排[left, div-1]
QuickSort(a, left, div-1);
// 递归排[div+1, right]
QuickSort(a, div+1, right);
}
前后指针版本
基本思路::需要两个指针,一个指针命名cur,一个指针命名prev;
- 选择数组的
第一个元素下标作为基准值key。 - 初始化两个指针cur和prev,分别指向数组的起始位置和起始位置的下一个位置。
当cur遇到比keyi的大的值以后,只需要++cur,因为他们之间的值都是比key大的值,- 如果
cur指针指向的元素小于基准值,先将prev指针向右移动一位,然后在将快指针指向的元素与慢指针指向的元素交换。 - 重复步骤3到步骤4,直到cur指针超出数组范围。结束循环.
将基准值的元素与prev指针位置的元素交换。此时基准值的左边元素都是比基准值小或者等于基准值,右边都比他大或者等于基准值。- 最后返回prev下标。
单趟排序:

-
为了更仔细的观看,我自己手动模拟一下,
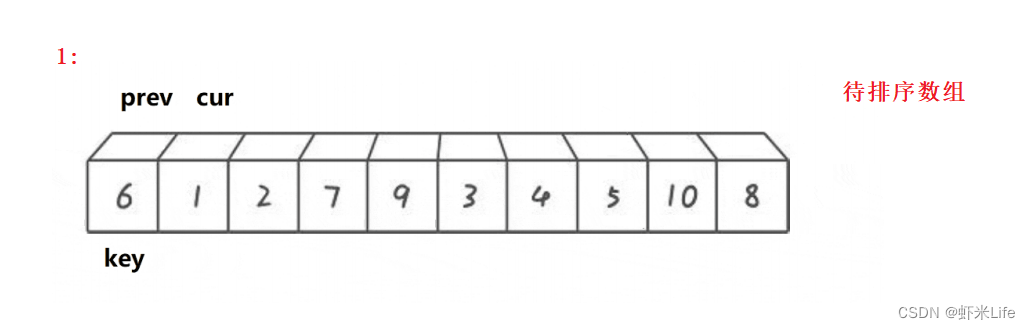
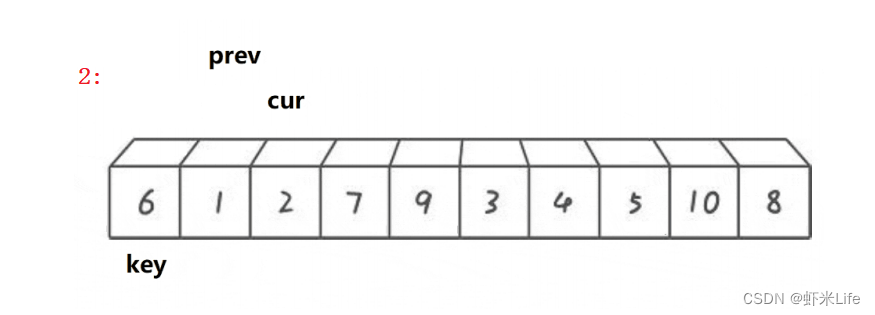
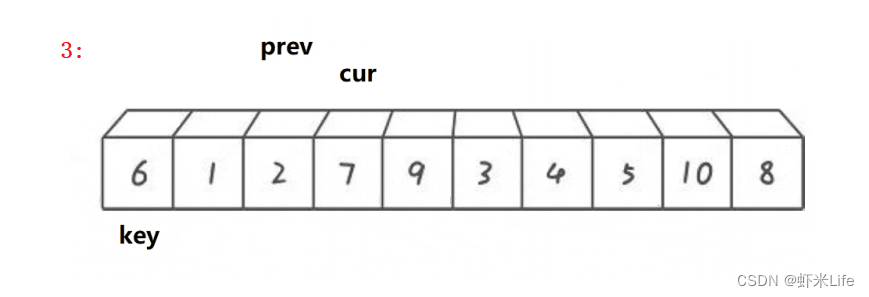
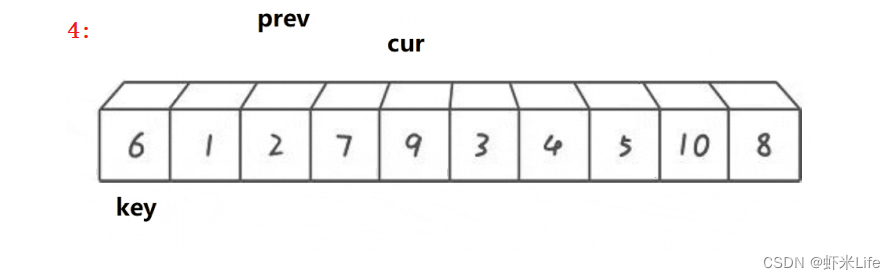
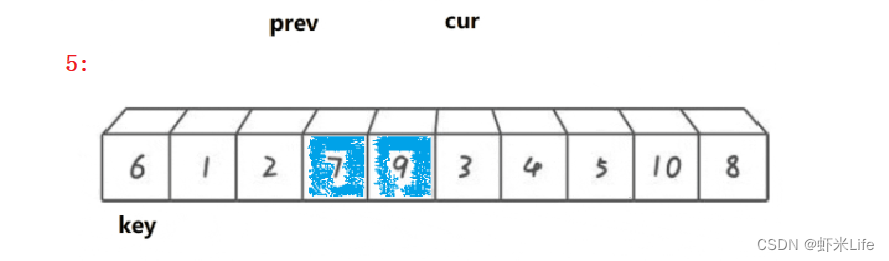
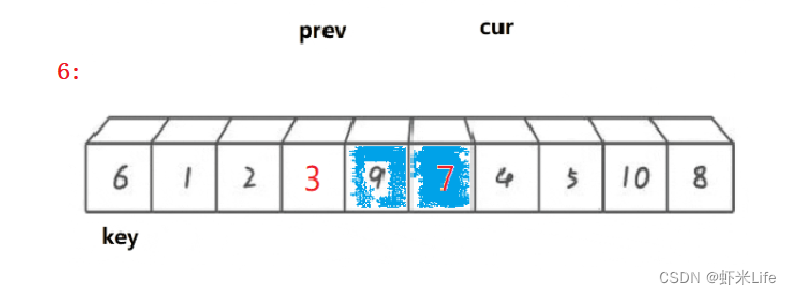
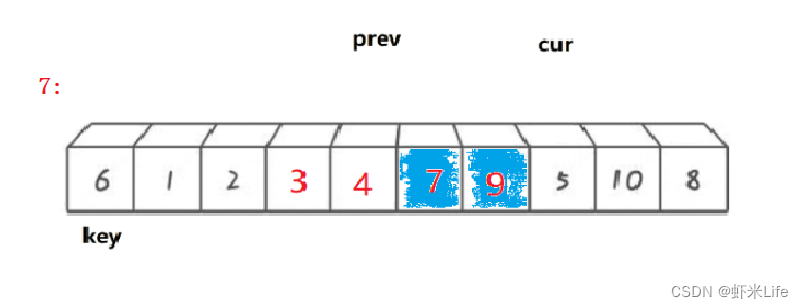
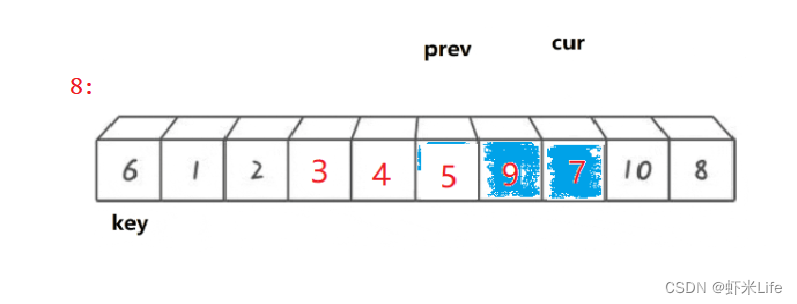
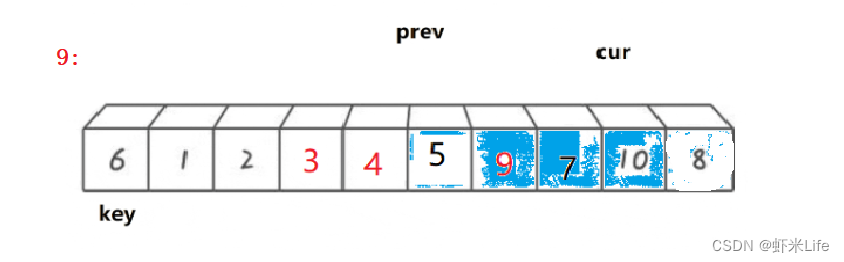
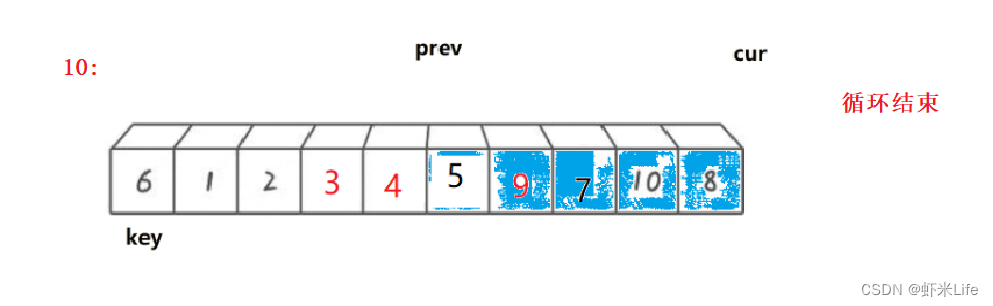
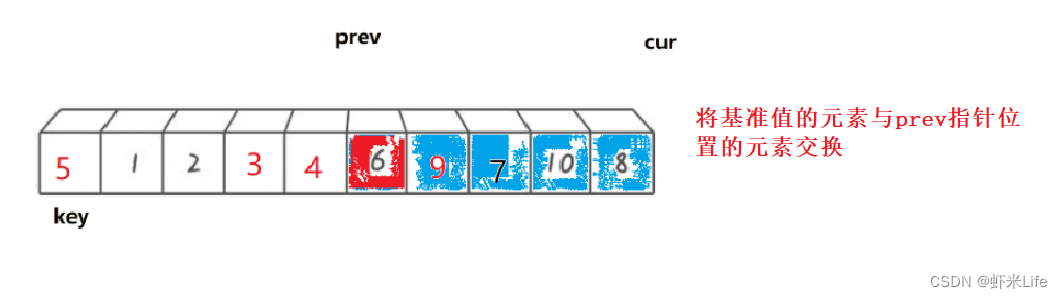
-
代码实现
// 前后指针版本
int Part_Sort3(int* a, int left, int right)
{
int keyi = left; // 基准值的索引
int prev = left; // 前指针
int cur = left + 1; // 后指针
while (cur <= right)
{
//如果当前元素小于基准值,将其与前指针指向的元素交换,并移动前指针
if (a[cur] < a[keyi])
{
//这样写每次相同的元素都要交换
++prev;
swap(&a[prev], &a[cur]);
}
//可以优化成这样,这样相同下标位置的值就不用交换
/*if (a[cur] < a[keyi] && ++prev != cur)
{
swap(&a[prev], &a[cur]);
}*/
++cur;
}
swap(&a[prev], &a[keyi]); // 将基准值放到正确的位置上
return prev; // 返回基准值的索引
}
以上代码大家可以自己手动模拟一下,配合着代码相信你们会更加能吃透.
三路划分版本
快速排序的三路划分是为了解决数组中存在大量重复元素时,快速排序算法性能下降的问题。在传统的快速排序算法中,选择一个基准元素,将数组划分为两个子数组,其中一个子数组中的元素都小于基准元素,另一个子数组中的元素都大于基准元素,然后对两个子数组进行递归排序。
然而,当数组中存在大量重复元素时,传统的快速排序算法会导致不必要的比较和交换操作,从而降低算法的效率。三路划分的主要目的是将数组划分为三个部分,分别存放小于、等于和大于基准元素的元素,以减少不必要的比较和交换操作。
通过三路划分,可以将相等的元素集中在一起,减少了对相等元素的重复比较和交换操作,提高了算法的效率。尤其在面对存在大量重复元素的情况下,三路划分可以有效地改善快速排序的性能。
三路划分本质:
1、小的甩到左边,大的甩到右边
2、跟key相等的值推到中间
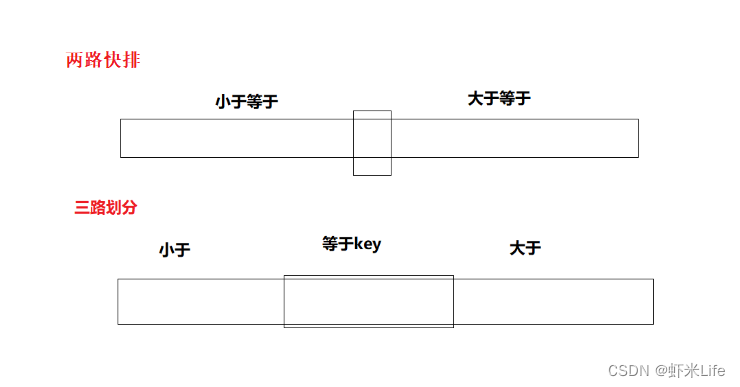
- 三路划分的基本思想是将数组分成三个部分,分别存放小于、等于和大于基准元素的元素。
基本思路:
- 选择一个基准元素。(通常是数组的第一个元素)
- 初始化三个指针:begin指针指向基准值的索引位置,cur指针指向begin + 1的位置,end指针指向数组末尾的位置
- 从数组的起始位置开始遍历到末尾位置。
a[c] < key如果当前元素小于基准元素,则将当前cur指针指向的元素交换到begin指针的位置,并将begin指针右移,cur指针右移。a[c] > key如果当前cur指针元素大于基准元素,则将当前cur指针指向元素交换到end指针的位置,并将end指针左移。由于交换后的元素是未经比较的新元素,所以cur指针不移动。a[c] == key如果当前元素等于基准元素,则将cur指针右移。- 重复步骤4-6,直到cur指针遇见end指针则遍历完成。循环结束。
- 最后, 数组被划分为了小于基准元素、等于基准元素和大于基准元素的三个部分。接下来,需要对小于和大于基准元素的两个部分分别进行递归排序。
- 对小于基准元素的部分进行递归排序:将小于基准元素的部分作为新的子数组,重复进行上述三路划分和递归排序的过程。
- 对大于基准元素的部分进行递归排序:将大于基准元素的部分作为新的子数组,重复进行上述三路划分和递归排序的过程。
-
代码实现 (因为有可能
划分出来是一个区间,我就直接在一个函数里面操作了,不封装其他函数来完成了) -
为了更仔细的体会,我自己手动模拟一下一组数据,

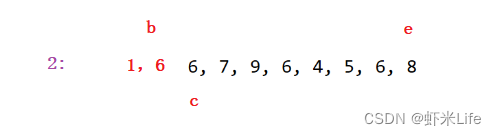


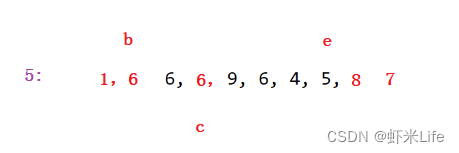

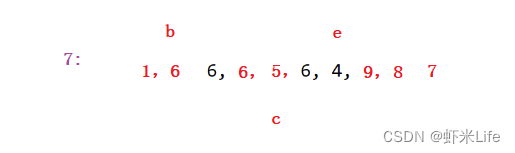
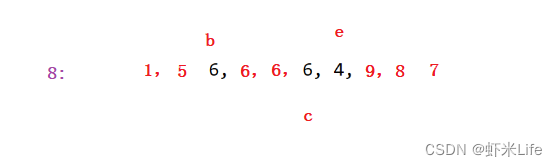

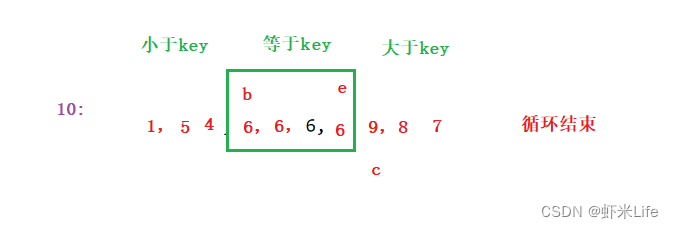
最后对小于和大于基准元素的两个部分分别进行递归排序。
//三路划分版本:解决数组中存在大量重复元素
//三路划分本质:
//1、小的甩到左边,大的甩到右边
//2、跟key相等的值推到中间
void Quicl_Sors_Dfp(int* a, int left, int right)
{
if (left >= right)
return;
int key = a[left];
int begin = left;
int cur = left + 1;
int end = right;
while (cur < end)
{
//a[c] < key,交换c和b位置的值,++b,++c
if (a[cur] < key)
{
swap(&a[cur], &a[begin]);
++cur;
++begin;
}
//a[c] > key,交换c和e位置的值,--e
else if (a[cur] > key)
{
swap(&a[cur], &a[end]);
--end;
}
//a[c] == key,++c
else
{
++cur;
}
}
//小 【b - e 相同】 大
//[left begin-1] [begin end] [end+1 right]
Quicl_Sors_Dfp(a, left, begin - 1);
Quicl_Sors_Dfp(a, end + 1, right);
}
非递归版本
快速排序是一种常用的排序算法,基于递归的实现方式是最常见的。然而,使用递归实现快速排序可能会导致栈溢出的问题,尤其在输入规模较大时。为了解决这个问题,可以使用栈来实现快速排序的非递归版本。
在非递归版本的快速排序中,栈被用来模拟递归调用的过程。具体而言,该算法使用一个栈来存储待排序子数组的起始和结束索引。通过迭代的方式将原本递归调用的过程转化为循环,避免了递归函数调用的开销。
算法的基本思想是::利用栈存储待排序子数组的起始和结束索引,在循环中每次从栈里面拿出一段区间单趟分割处理左右子区间入栈,将子数组划分为更小的子数组直到排序完成。
实现思路如下:
- 定义一个栈,用于记录每个待排序子数组的起始和终止索引。
- 将初始的起始索引和终止索引入栈,表示要对整个数组进行排序。
- 进入循环,直到栈为空
- 出栈得到当前子数组的起始和结束索引。
- 以子数组的第一个元素作为基准,对子数组进行划分,将小于基准的元素放在基准的左侧,大于基准的元素放在基准的右侧。
- 如果基准元素的左侧仍有未排序的元素,将其起始索引和终止索引入栈;
-如果基准元素的右侧仍有未排序的元素,将其起始索引和终止索引入栈。 - 如果划分后得到的左右子数组的长度大于1,则将它们的起始和结束索引依次入栈。
- 当栈为空时,排序完成。
- 为了更仔细的体会,我自己手动模拟一下部分数据,



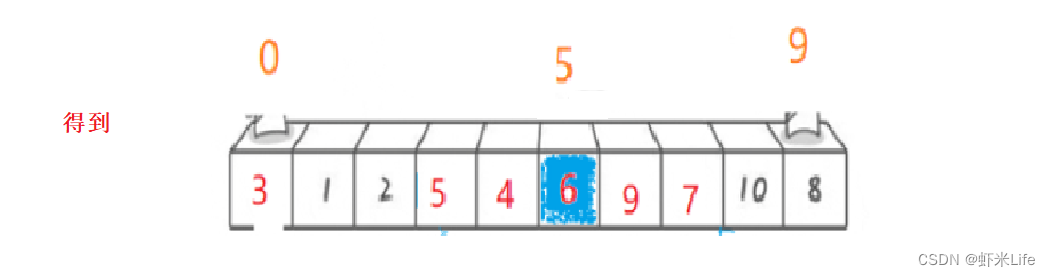

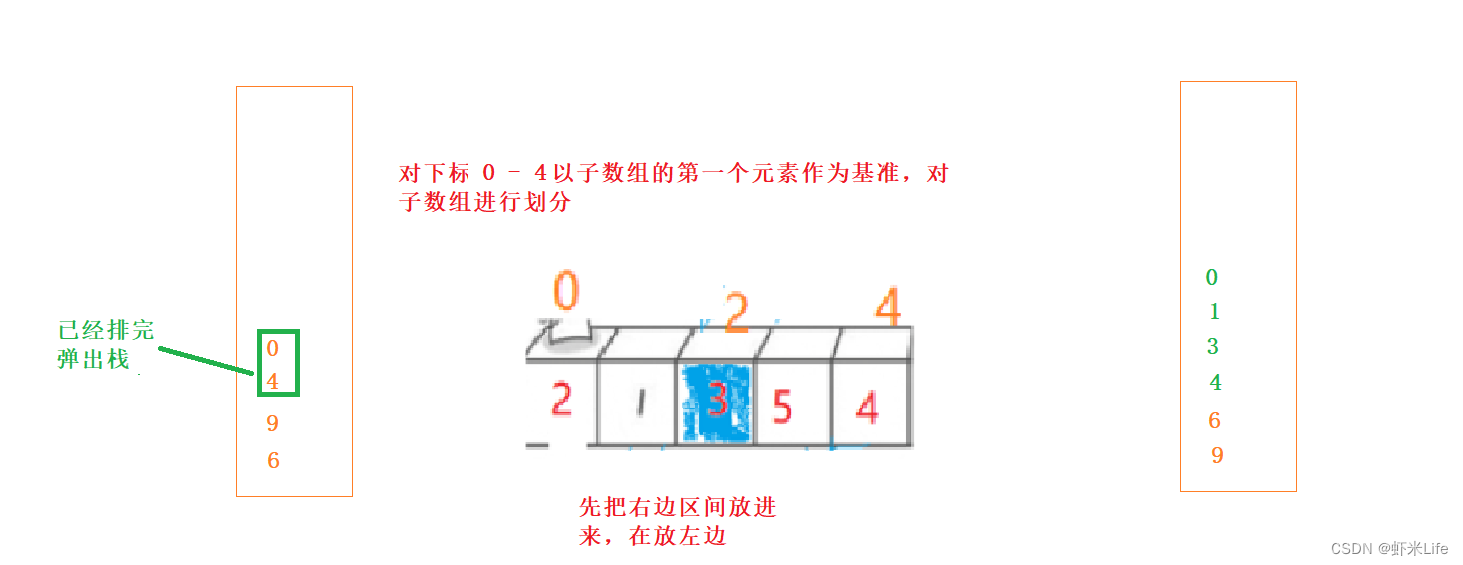
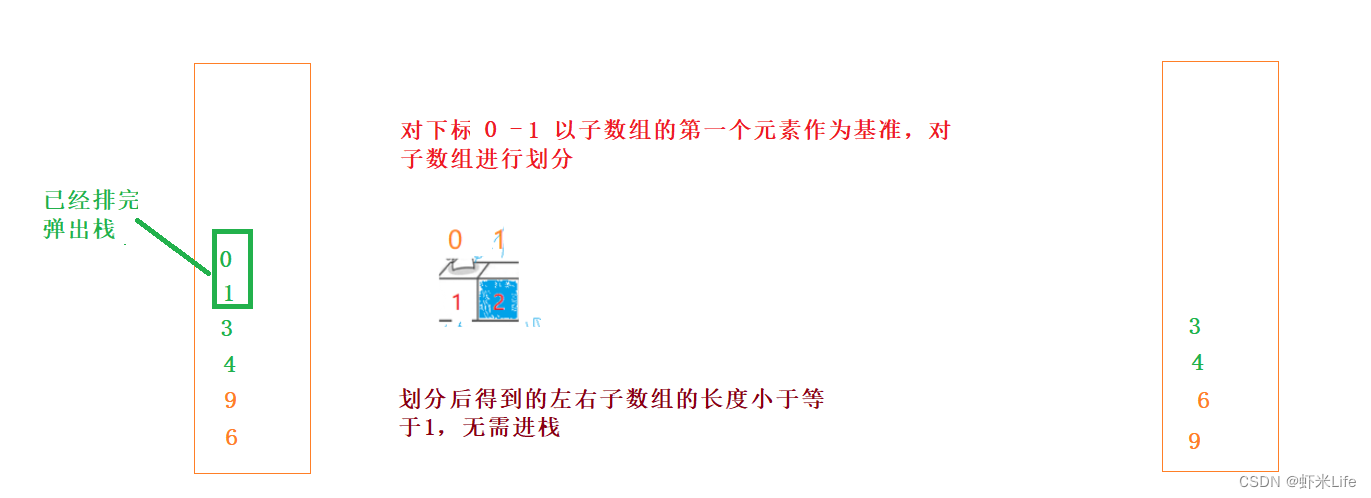
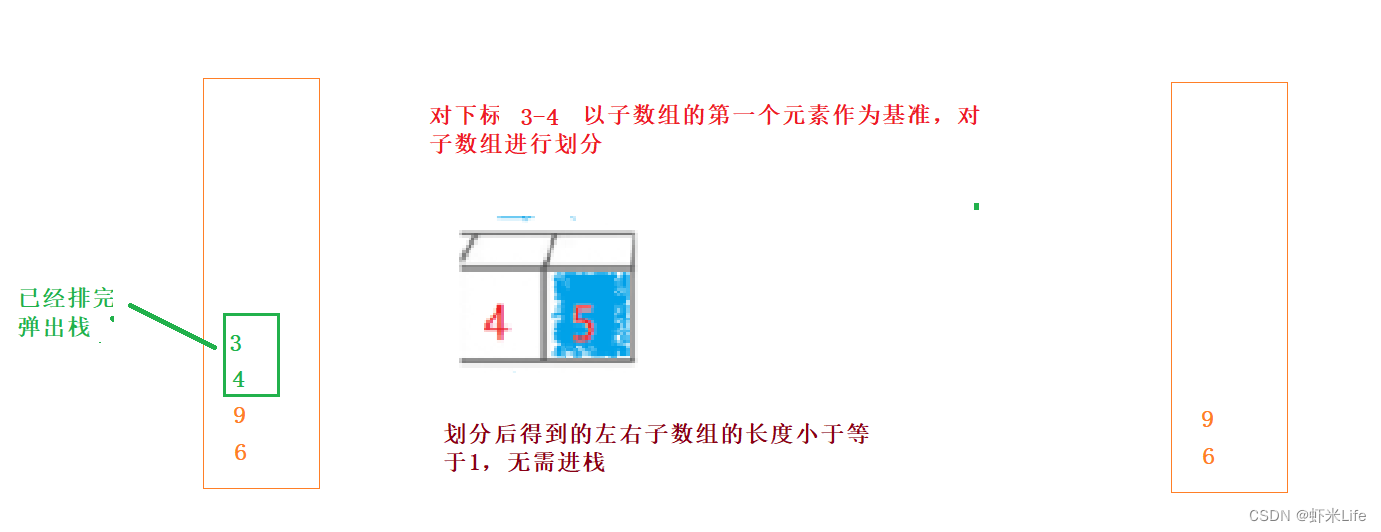

- 代码实现(栈的代码这里就不写了,如需要看的可以到我这个文章看写我的栈实现与细节)
【数据结构】一篇带你彻底了解栈
// 非递归版本的快速排序
void Quick_SortNoR(int* a, int left, int right)
{
ST s1; // 定义一个存储左右边界的栈 s1
STinit(&s1); // 初始化栈 s1
// 将初始左右边界入栈
STPush(&s1, right);
STPush(&s1, left);
while (!STEmpty(&s1))
{
int begin = StackTop(&s1); // 取出栈顶的左边界
StackPop(&s1); // 弹出栈顶元素
int end = StackTop(&s1); // 取出栈顶的右边界
StackPop(&s1); // 弹出栈顶元素
int keyi = Part_Sort3(a, begin, end); // 对当前区间进行三数取中分区,并返回基准值的位置 keyi
// [begin, keyi-1] keyi [keyi+1, end]
if (keyi + 1 < end)
{
STPush(&s1, end); // 将当前基准值右边的边界入栈
STPush(&s1, keyi + 1); // 将当前基准值右边的边界入栈,准备分区
}
if (keyi - 1 > begin)
{
STPush(&s1, keyi - 1); // 将当前基准值左边的边界入栈,准备分区
STPush(&s1, begin); // 将当前基准值左边的边界入栈
}
}
STDestroy(&s1); // 销毁栈 s1
}
这样,使用栈的非递归方式可以实现快速排序的算法思想,避免了递归带来的函数调用开销,同时保持了快速排序的效率。
快速排序优化
1. 三数取中法选key
当数组接近有序,快速排序会变的变成非常糟糕,时间复杂度是O(N^2)。
每次选择的基准元素可能会导致分割得到的左右子序列的大小差异很大,从而使得快速排序的效率下降。
具体来说,当数组接近有序时,快速排序的分割操作可能会将一个较小的元素放在一个较大的元素的右边,或者将一个较大的元素放在一个较小的元素的左边。这样一来,在每一次划分操作后,都会有一个较小的子序列和一个较大的子序列。如果这种情况持续发生,那么快速排序就会退化成类似于冒泡排序的过程,每次只能将一个元素放到它最终的位置上,排序的效率会大大降低。
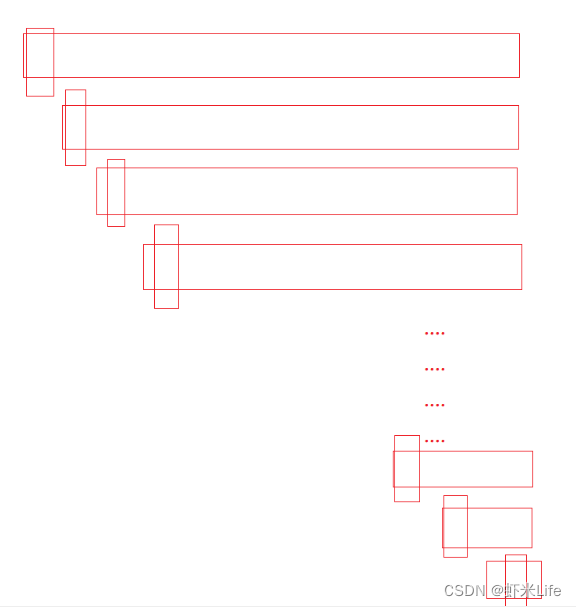
为了解决这个问题,可以采用一些优化策略,如随机选择基准元素、三数取中法选择基准元素等,以尽量避免最坏情况的发生。我们这里就说下三数取中优化.
-
在三数取中法中,我们需要选择三个数来确定基准元素。通常情况下,我们选择子序列的第一个元素、中间元素和最后一个元素作为候选的三个数。
具体步骤如下:
-
找到子序列的中间位置,即 (起始索引 + 结束索引) / 2。
-
比较子序列的第一个元素、中间元素和最后一个元素的大小。
-
选择这三个元素中的中间大小的元素作为基准元素。
-
返回下标
-
-
代码实现
// 三数取中法选择基准元素的索引
int GetMidIndex(int* a, int left, int right)
{
// 计算中间位置的索引
int mid = (left + right) / 2;
if (a[left] < a[mid])
{
// a[left] < a[mid] < a[right]
if (a[mid] < a[right])
return mid;
// a[left] < a[right] < a[mid]
else if (a[right] > a[left])
return right;
else
return left;
}
else // a[left] > a[mid]
{
// a[left] > a[mid] > a[right]
if (a[mid] > a[right])
return mid;
// a[left] > a[right] > a[mid]
else if (a[left] > a[right])
return right;
else
return left;
}
}
有的同学又有疑问,我加了三数取中,前面的代码是不是都要改。
其实并不需要,在GetMidIndex(a, left, right) 函数会返回一个基准值的索引,表示选择了基准值的位置。
在调用下交换函数swap(&a[left], &a[midIndex]) 将选择的基准值与数组的最左边元素 a[left] 进行交换。这样做是为了符合快速排序算法中的约定,即将基准值放在数组的最左边位置。
各版本的加上三数取中优化的代码
- Hoare版本
// Hoare版本
int Part_Sort1(int* a, int left, int right)
{
int midIndex = GetMidIndex(a, left, right); // 获取基准值的索引
swap(&a[left], &a[midIndex]); // 将基准值移到数组最左边
int keyi = left; // 基准值的索引
while (left < right)
{
// 右边找小于基准值的元素
while (left < right && a[right] >= a[keyi])
{
right--;
}
// 左边找大于基准值的元素
while (left < right && a[left] <= a[keyi])
{
left++;
}
swap(&a[left], &a[right]); // 交换左右两边的元素
}
swap(&a[keyi], &a[right]); // 将基准值放到正确的位置上
return right; // 返回基准值的索引
}
- 挖坑法
// 挖坑法
int Part_Sort2(int* a, int left, int right)
{
int midIndex = GetMidIndex(a, left, right); // 获取基准值的索引
swap(&a[left], &a[midIndex]); // 将基准值移到数组最左边
int key = a[left]; // 基准值
int tmp = left; // 坑的位置
while (left < right)
{
// 右边找小于基准值的元素
while (left < right && a[right] >= key)
{
right--;
}
a[tmp] = a[right]; // 将找到的元素放入坑中
tmp = right;
// 左边找大于基准值的元素
while (left < right && a[left] <= key)
{
left++;
}
a[tmp] = a[left]; // 将找到的元素放入坑中
tmp = left;
}
a[tmp] = key; // 将基准值放入坑中
return tmp; // 返回基准值的索引
}
- 前后指针版本
// 前后指针版本
int Part_Sort3(int* a, int left, int right)
{
int midIndex = GetMidIndex(a, left, right); // 获取基准值的索引
swap(&a[left], &a[midIndex]); // 将基准值移到数组最左边
int keyi = left; // 基准值的索引
int prev = left; // 前指针
int cur = left + 1; // 后指针
while (cur <= right)
{
// 如果当前元素小于基准值,将其与前指针指向的元素交换,并移动前指针
if (a[cur] < a[keyi] && ++prev != cur)
{
swap(&a[prev], &a[cur]);
}
//这样写每次相同的元素都要交换
/* if (a[cur] < a[keyi])
{
++prev;
swap(&a[prev], &a[cur]);
}*/
++cur;
}
swap(&a[prev], &a[keyi]); // 将基准值放到正确的位置上
return prev; // 返回基准值的索引
}
- 三路划分版本
void Quicl_Sors_Dfp(int* a, int left, int right)
{
if (left >= right)
return;
int midIndex = GetMidIndex(a, left, right); // 获取基准值的索引
swap(&a[left], &a[midIndex]); // 将基准值移到数组最左边
int key = a[left];
int begin = left;
int cur = left + 1;
int end = right;
while (cur < end)
{
//a[c] < key,交换c和b位置的值,++b,++c
if (a[cur] < key)
{
swap(&a[cur], &a[begin]);
++cur;
++begin;
}
//a[c] > key,交换c和e位置的值,--e
else if (a[cur] > key)
{
swap(&a[cur], &a[end]);
--end;
}
//a[c] == key,++c
else
{
++cur;
}
}
//小 【b - e 相同】 大
//[left begin-1] [begin end] [end+1 right]
Quicl_Sors_Dfp(a, left, begin - 1);
Quicl_Sors_Dfp(a, end + 1, right);
}
2. 递归到小的子区间时,可以考虑使用插入排序
在快速排序算法中,当子区间的大小足够小时,可以考虑使用插入排序来代替递归调用。这是因为插入排序在处理小规模数据时具有较好的性能。
当子区间的大小较小时,递归调用的开销可能会比排序本身的开销更大,因为递归调用需要额外的函数调用和栈空间的使用。而插入排序是一种简单且高效的排序算法,对于小规模的数据集,它的性能优于快速排序。
在实践中,可以通过设置一个阈值来决定是否使用插入排序。当子区间的大小小于阈值时,使用插入排序;否则,继续使用快速排序进行递归划分。
使用插入排序的优点是它对于部分有序的数据集具有较好的性能,因为插入排序每次将一个元素插入到已排序的序列中,对于有序度较高的数据集,插入排序的比较和移动操作会较少。
总而言之,使用插入排序来替代递归调用的快速排序可以在处理小规模数据时提高性能,并减少递归调用的开销。这是一种常见的优化策略,可以根据实际情况进行调整和实现。
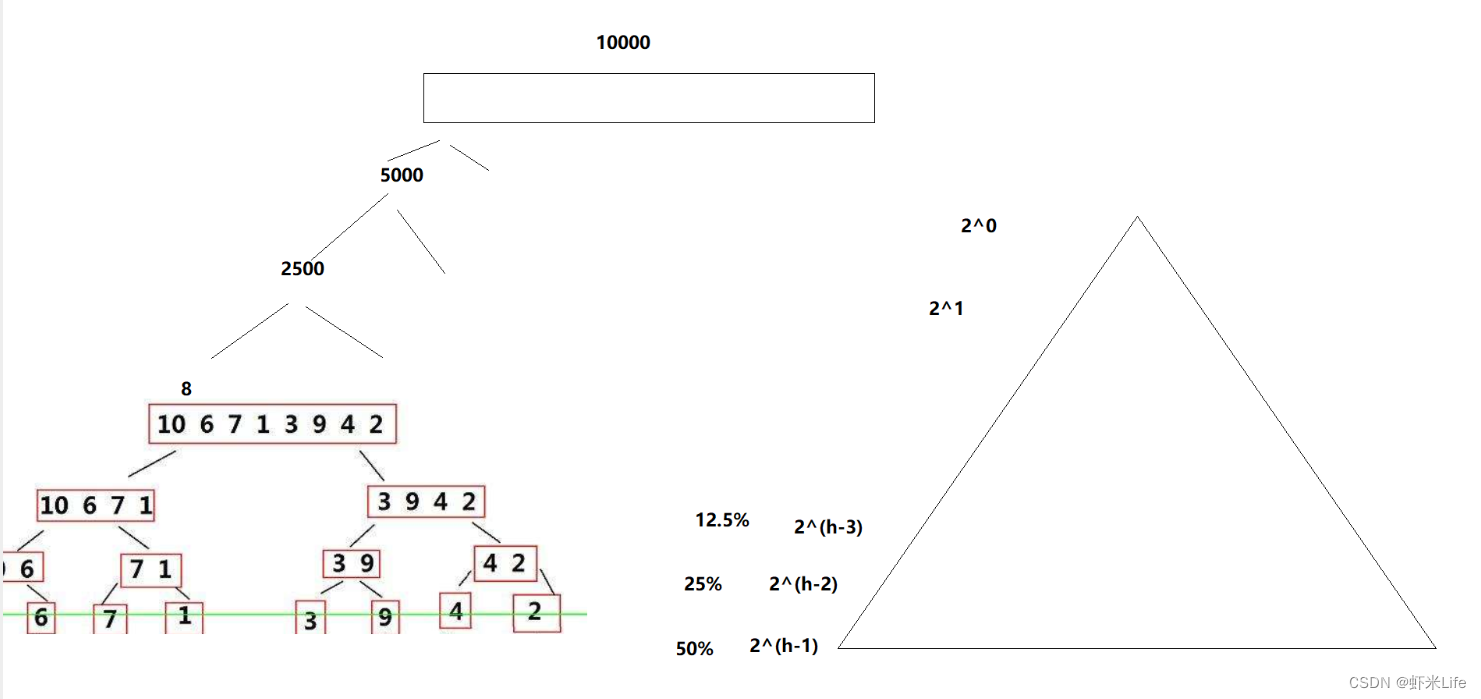
在使用递归调用的快速排序算法中,对于10000个数的排序,当阈值为10时,我们可以估计一下在使用插入排序的情况下可以节约多少栈空间的使用。
假设每个子区间的大小平均为10(小于阈值),那么在使用插入排序的情况下,总共会有10000个数 / 10 = 1000个子区间。大约节省了77.5%的. 所以小区间优化还是很有必要的.
- 代码实现 插入排序我也不写了,具体实现请看该文章
“插入排序:小数据量排序的王者“
// 快速排序
// 时间复杂度: O(logN*N)
// 空间复杂度:O(logN)
void Quick_Sort(int* a, int left, int right)
{
if (left >= right)
return;
int keyi = Part_Sort3(a, left, right); // 获取基准值的索引
// [begin, keyi-1] keyi [keyi+1, end]
// 对基准值左边的子数组进行快速排序
// Quick_Sort(a, left, keyi - 1);
// 对基准值右边的子数组进行快速排序
// Quick_Sort(a, keyi + 1, right);
//快排:: 小区间优化 因为插入排序在小数组上的性能往往比快速排序更好。
if (keyi - left > 10)
{
// 对基准值左边的子数组进行快速排序
Quick_Sort(a, left, keyi - 1);
}
else
{
InsertSort(a + left, keyi - 1 - left + 1);
}
if (right - keyi > 10)
{
// 对基准值右边的子数组进行快速排序
Quick_Sort(a, keyi + 1, right);
}
else
{
InsertSort(a + keyi + 1, right - keyi + 1 - 1);
}
}
快速排序的特性总结:
快速排序是一种高效的排序算法,其核心思想是通过分治的策略将一个大问题分解为若干个小问题,并通过递归等方式解决这些小问题。
- 快速排序整体的综合性能和使用场景都是比较好的,所以才敢叫快速排序
- 时间复杂度:O(N*logN)
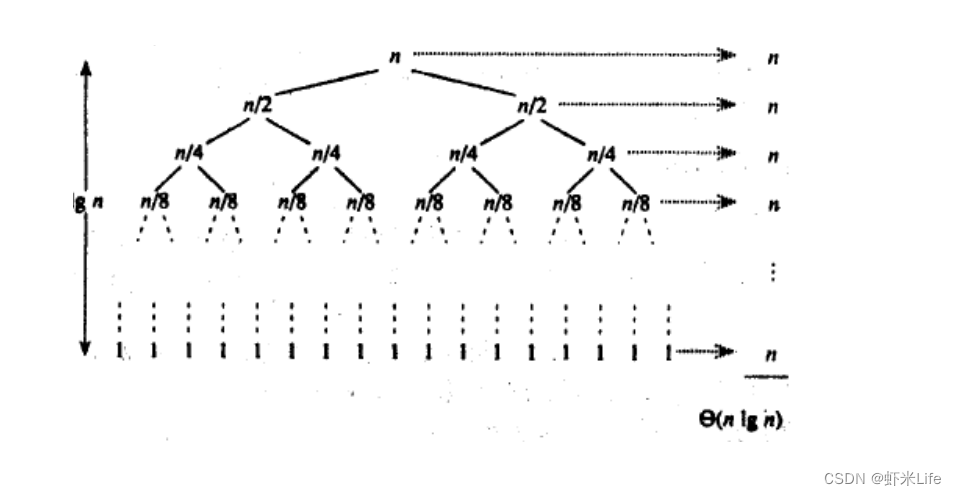
- 空间复杂度:O(logN)
- 稳定性:不稳定
稳定性是什么:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定的。
在快速排序中:元素的交换是通过比较和交换来实现的,不保证相等元素的相对顺序不变。当基准元素与其他元素进行比较并交换位置时,相同元素的相对顺序可能会改变。