目录
代码
jstack
分析
什么是哈希表
在讨论哈希表之前,我们先大概了解下其他数据结构在新增,查找等基础操作执行性能
数组:采用一段连续的存储单元来存储数据。对于指定下标的查找,时间复杂度为O(1);通过给定值进行查找,需要遍历数组,逐一比对给定关键字和数组元素,时间复杂度为O(n),当然,对于有序数组,则可采用二分查找,插值查找,斐波那契查找等方式,可将查找复杂度提高为O(logn);对于一般的插入删除操作,涉及到数组元素的移动,其平均复杂度也为O(n)
线性链表:对于链表的新增,删除等操作(在找到指定操作位置后),仅需处理结点间的引用即可,时间复杂度为O(1),而查找操作需要遍历链表逐一进行比对,复杂度为O(n)
二叉树:对一棵相对平衡的有序二叉树,对其进行插入,查找,删除等操作,平均复杂度均为O(logn)。
哈希表:相比上述几种数据结构,在哈希表中进行添加,删除,查找等操作,性能十分之高,不考虑哈希冲突的情况下(后面会探讨下哈希冲突的情况),仅需一次定位即可完成,时间复杂度为O(1),接下来我们就来看看哈希表是如何实现达到惊艳的常数阶O(1)的。
我们知道,数据结构的物理存储结构只有两种:顺序存储结构和链式存储结构(像栈,队列,树,图等是从逻辑结构去抽象的,映射到内存中,也这两种物理组织形式),而在上面我们提到过,在数组中根据下标查找某个元素,一次定位就可以达到,哈希表利用了这种特性,哈希表的主干就是数组。
比如我们要新增或查找某个元素,我们通过把当前元素的关键字 通过某个函数映射到数组中的某个位置,通过数组下标一次定位就可完成操作。
这个函数可以简单描述为:存储位置 = f(关键字) ,这个函数f一般称为哈希函数,这个函数的设计好坏会直接影响到哈希表的优劣。
hashmap在并发执行put操作时会引起死循环,因为在put中会引起扩容操作,使链表形成环形的数据结构,不是很明白,然后在网上看了一些博客,但是博客都是jdk1.7版本的,而1.8版本中的扩容操作已经和1.7版本中大不一样了,于是自己开始研究,看源码的时候,觉得jdk1.8版本中多线程put不会在出现死循环问题了,只有可能出现数据丢失的情况,因为1.8版本中,会将原来的链表结构保存在节点e中,然后依次遍历e,根据hash&n是否等于0,分成两条支链,保存在新数组中。jdk1.7版本中,扩容过程中会新数组会和原来的数组有指针引用关系,所以将引起死循环问题。
jdk1.8的HashMap在多线程的情况下也会出现死循环的问题,但是1.8是在链表转换树或者对树进行操作的时候会出现线程安全的问题。
复习一下线程安全的定义:
在拥有共享数据的多条线程并行执行的程序中,线程安全的代码会通过同步机制保证各个线程都可以正常且正确的执行,不会出现数据污染等意外情况。
代码
类名字我忘记改了这是我以前看park时候弄的但是这不重要
当你运行
public class parkAndUnpark {
static Map<String,String> map = new HashMap<>();
static class MyTask implements Runnable{
int start = 0;
public MyTask(int start){
this.start = start;
}
@Override
public void run() {
for(int i = start ; i<10000000;i+=2){
map.put(Integer.toString(i),Integer.toBinaryString(i));
System.out.println(i);
}
}
}
public static void main(String[] args) throws InterruptedException {
Thread t1 = new Thread(new MyTask(0));
Thread t2 = new Thread(new MyTask(1));
t1.start();
t2.start();
//主线程等待两个线程执行完
t1.join();
t2.join();
System.out.println(map.size());
}
}
好了这里会阻塞住
但是可能你没阻塞住所以多运行几次
实验jps查看运行线程

jstack
使用jstack分析堆栈快照
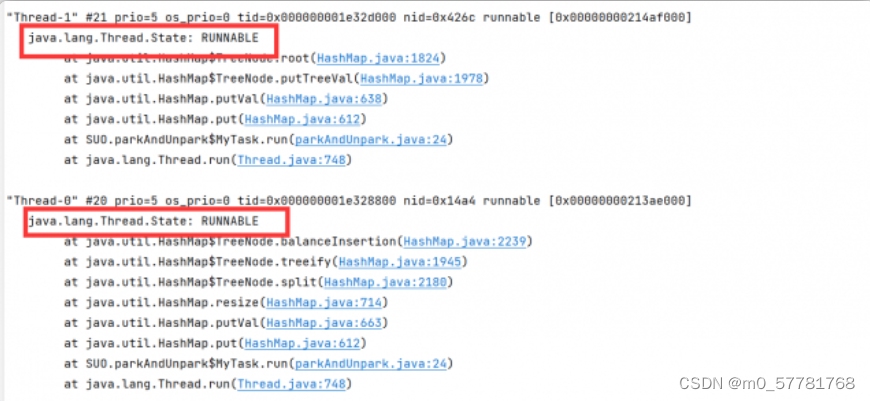
两个线程都在运行但是没有输出同时也没有结束这就产生了死循环,所以分析
分析
分析balanceInsertion 方法,上面就可以看到
static <K,V> TreeNode<K,V> balanceInsertion(TreeNode<K,V> root,
TreeNode<K,V> x) {
//新插入的节点标为红色
x.red = true;
//无限for循环,定义xp、xpp、xppl、xppr变量,在循环体进行赋值,p就是parents
//- root:当前根节点
//- x :新插入的节点
//- xp :新插入节点的父节点
//- xpp :新插入节点的祖父节点
//- xppl:新插入节点的左叔叔节点
//- xppr:新插入节点的右叔叔节点
for (TreeNode<K,V> xp, xpp, xppl, xppr;;) {
//为定义的各个变量赋值的过程
if ((xp = x.parent) == null) {
x.red = false;
return x;
}
else if (!xp.red || (xpp = xp.parent) == null)
return root;
//重点看这里
//如果父节点是爷爷节点的左孩子
if (xp == (xppl = xpp.left)) {
//如果右叔叔不为空且为红色
if ((xppr = xpp.right) != null && xppr.red) {
//右叔叔变为黑色
xppr.red = false;
//父节点变为黑色
xp.red = false;
//爷爷节点变为黑色
xpp.red = true;
//将爷爷节点当作起始节点,再次循环,请注意再次循环!!!
x = xpp;
}
//省略其他代码
}
总的来说上边的源码就是,新插入一个节点,该方法要保持红黑树的五个性质
性质1. 节点是红色或黑色。
性质2. 根节点是黑色。
性质3 每个叶节点(NIL节点,空节点)是黑色的。
性质4 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)
性质5. 从任一节点到其每个叶子的路径上包含的黑色节点数量都相同。