一.数据预处理
由于神经网络输入数据的范围可能特别大,导致神经网络收敛慢、训练时间长。因此在训练神经网络前一般对数据进行预处理(不妨假设这里的指标都是效益型的(即都是正项指标)),一种重要的预处理的处理手段是归一化处理,就是将数据映射到[0,1]或者[-1,1]区间。
设 x x x为规格化前的数据 , x m i n 和 x m a x ,x_{min}和x_{max} ,xmin和xmax为 x x x的最大值和最小值; x ~ \tilde{x} x~为规格化后的数据, x ˉ \bar{x} xˉ为 x x x的平均值, s s s为 x x x的标准差,用python计算标准差时,需要表明自由度是 n n n还是 n − 1 n-1 n−1(参数ddof=0自由度为 n n n,ddof=1自由度为 n − 1 n-1 n−1)
第一种归一化的线性变换为:
x
~
=
x
−
x
m
i
n
x
m
a
x
−
x
min
(1)
\tilde{x}=\frac{x-x_{min}}{x_{max}-x_{\min}}\tag{1}
x~=xmax−xminx−xmin(1)
该归一化处理一般适用于激活函数是sigmoid函数时。
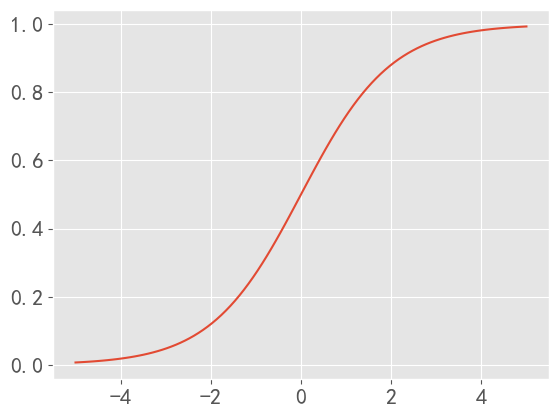
sigmoid函数:
sigmoid函数也叫Logistic函数,用于隐层神经元输出,取值范围为(0,1),它可以将一个实数映射到(0,1)的区间,可以用来做二分类。在特征相差比较复杂或是相差不是特别大时效果比较好。Sigmoid作为激活函数有以下优缺点:
优点:平滑、易于求导。
缺点:激活函数计算量大,反向传播求误差梯度时,求导涉及除法;反向传播时,很容易就会出现梯度消失的情况,从而无法完成深层网络的训练。
Sigmoid函数由下列公式定义:
S ( x ) = 1 1 + e − x S(x)=\frac{1}{1+e^{-x}} S(x)=1+e−x1
其导数可用原函数来表示:
S ′ ( x ) = e − x ( 1 + e − x ) 2 = S ( x ) ( 1 − S ( x ) ) S^{\prime}(x)=\frac{e^{-x}}{\left(1+e^{-x}\right)^{2}}=S(x)(1-S(x)) S′(x)=(1+e−x)2e−x=S(x)(1−S(x))
sigmoid函数曲线如下:
参考文章:sigmoid函数,百度百科
第二种归一化的线性变换为:
x
~
=
2
x
−
(
x
m
i
n
+
x
max
)
x
m
a
x
−
x
min
=
2
(
x
−
x
min
)
x
m
a
x
−
x
min
−
1
(2)
\tilde{x}=\frac{2x-\left( x_{min}+x_{\max} \right)}{x_{max}-x_{\min}}=\frac{2\left( x-x_{\min} \right)}{x_{max}-x_{\min}}-1\tag{2}
x~=xmax−xmin2x−(xmin+xmax)=xmax−xmin2(x−xmin)−1(2)
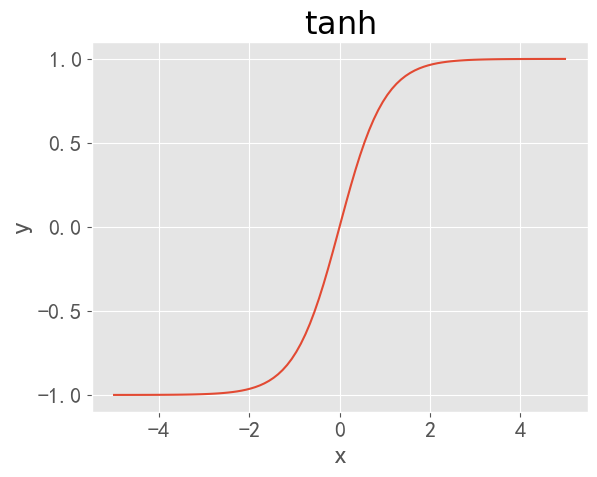
上述公式将数据映射到区间[-1,1]上,一般激活函数是 tanh \tanh tanh函数时。
tanh函数相较于sigmoid函数要更加常见一些,该函数将区间 ( − ∞ , ∞ ) (-\infty,\infty) (−∞,∞)映射到 ( − 1 , 1 ) (-1,1) (−1,1)
改公式为:
f ( u ) = e u − e − u e u + e − u f\left( u \right) =\frac{e^u-e^{-u}}{e^u+e^{-u}} f(u)=eu+e−ueu−e−u
函数图像为:
数据预处理也可以进行一般的标准化处理:
x
~
=
x
−
x
ˉ
s
(3)
\tilde{x}=\frac{x-\bar{x}}{s}\tag{3}
x~=sx−xˉ(3)
二.引用举例
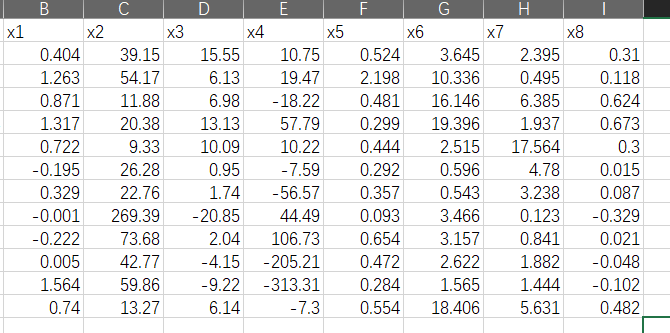
我国沪、深两市上市公司中有非ST公司和ST公司,一般而言非ST公司的信用等级较高,ST公司的信用等级较差。为有效评价上市公司信用,建立了上市公司信用评价指标如下:流动比率 x 1 x_1 x1,负债比率 x 2 x_2 x2,存货周转率 x 3 x_3 x3,总资产周转率 x 4 x_4 x4,净资产收益率 x 5 x_5 x5,每股收益率 x 6 x_6 x6,总利润增长率 x 7 x_7 x7,每股经营现金流量 x 8 x_8 x8。已知训练样本和待判样本的数据如表15.9所列,其中类别中的值1表示是ST公司,0表示不是ST公司。
我把数据放在了这里:点击“我”即可,我是svip应该不会失效
提取码:6666
| 序号 | x 1 x_1 x1 | x 2 x_2 x2 | x 3 x_3 x3 | x 4 x_4 x4 | x 5 x_5 x5 | x 6 x_6 x6 | x 7 x_7 x7 | x 8 x_8 x8 | 类别 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.404 | 39.15 | 15.55 | 10.75 | 0.524 | 3.645 | 2.395 | 0.31 | 0 |
| 2 | 1.263 | 54.17 | 6.13 | 19.47 | 2.198 | 10.336 | 0.495 | 0.118 | 0 |
| 3 | 0.871 | 11.88 | 6.98 | -18.22 | 0.481 | 16.146 | 6.385 | 0.624 | 0 |
| 4 | 1.317 | 20.38 | 13.13 | 57.79 | 0.299 | 19.396 | 1.937 | 0.673 | 0 |
| 5 | 0.722 | 9.33 | 10.09 | 10.22 | 0.444 | 2.515 | 17.564 | 0.3 | 0 |
| 6 | -0.195 | 26.28 | 0.95 | -7.59 | 0.292 | 0.596 | 4.78 | 0.015 | 1 |
| 7 | 0.329 | 22.76 | 1.74 | -56.57 | 0.357 | 0.543 | 3.238 | 0.087 | 1 |
| 8 | -0.001 | 269.39 | -20.85 | 44.49 | 0.093 | 3.466 | 0.123 | -0.329 | 1 |
| 9 | -0.222 | 73.68 | 2.04 | 106.73 | 0.654 | 3.157 | 0.841 | 0.021 | 1 |
| 10 | 0.005 | 42.77 | -4.15 | -205.21 | 0.472 | 2.622 | 1.882 | -0.048 | 1 |
| 11 | 1.564 | 59.86 | -9.22 | -313.31 | 0.284 | 1.565 | 1.444 | -0.102 | 待判 |
| 12 | 0.74 | 13.27 | 6.14 | -7.3 | 0.554 | 18.406 | 5.631 | 0.482 | 待判 |
解:对于正项指标(效益型指标)
x
1
,
x
3
,
x
4
,
x
5
,
x
6
,
x
7
,
x
8
x_1,x_3,x_4,x_5,x_6,x_7,x_8
x1,x3,x4,x5,x6,x7,x8,利用公式
x
~
=
x
i
−
x
i
m
i
n
x
i
m
a
x
−
x
i
m
i
n
,
i
=
1
,
3
,
4
,
5
,
6
,
7
,
8
\tilde{x}=\frac{x_i-x_{i}^{min}}{x_{i}^{max}-x_{i}^{min}},i=1,3,4,5,6,7,8
x~=ximax−ximinxi−ximin,i=1,3,4,5,6,7,8
进行数据标准化处理,对逆向指标(成本型指标)
x
2
x_2
x2,利用公式
x
~
2
=
x
2
m
i
n
−
x
2
x
2
m
a
x
−
x
2
m
i
n
\tilde{x}_2=\frac{x_{_2}^{min}-x_2}{x_{_2}^{max}-x_{_2}^{min}}
x~2=x2max−x2minx2min−x2
进行数据标准化处理,其中 x i m i n 和 x i m a x x_{i}^{min}和x_{i}^{max} ximin和ximax分别代表数据 x i x_i xi的最小值和最大值
我们构造的BP神经元网络只有一个隐层,隐藏神经元的个数为30,激活函数为sigmoid函数,编写程序如下:
注:如果出现代码不能运行的情况,请跳到最后查看可能的解决方法
# coding=utf-8
'''
author:chuanshana
email:2505647237@qq.com
'''
import pandas as pd
from sklearn.neural_network import MLPClassifier
import numpy as np
# 加载数据
data = pd.read_csv("D:\Pycharm\math_machine\公司数据.csv", index_col=0)
# 提取训练样本数据和待判样本数据
train_x = data.loc[:10, :] # 这就是前9行数据
judge_data = data.loc[10:, :] # 待判断数据
print(judge_data)
# 逐列计算最大值和最小值
x_max = train_x.max(axis=0)
x_min = train_x.min(axis=0) # 如果axis=1就是计算每一行的最大值和最小值
print(x_max, "\n", x_min)
# 使用归一化对数据进行处理
# 注意注意,这里我们要转化一下数据类型,不然可能会报错,字符串与字符串无法使用减号
#train_x = train_x.apply(pd.to_numeric)
#x_min = x_min.apply(pd.to_numeric)
#judge_data = judge_data.apply(pd.to_numeric)
#x_max = x_max.apply(pd.to_numeric) # 到这数据转换完毕
standardization = (train_x - x_min) / (x_max - x_min)
# 这里的x2是逆向指标,我们需要做额外的标准化:
standardization.iloc[:, 1] = (x_min[1] - train_x.iloc[:, 1]) / (x_max[1] - x_min[1]) # 到此我们的训练集数据标准化完成
y_0 = np.hstack([np.zeros(5), np.ones(5)]) # 标号值,5个0,5个1
print("训练集数据标准化已完成", "\n", standardization)
# 构造并拟合模型
model = MLPClassifier(solver="lbfgs", activation="logistic", hidden_layer_sizes=30).fit(standardization, y_0)
# 待判数据标准化
judge_data = (judge_data - x_min) / (x_max - x_min)
# 同样第二列特殊处理
judge_data.iloc[:, 1] = (x_min[1] - judge_data.iloc[:, 1]) / (x_max[1] - x_min[1])
# 进行预测
y_predict = model.predict(judge_data)
print("待判样本类别", y_predict,
"\n", "属于各个样本的概率", model.predict_proba(standardization), "\n", "训练样本的回带正确率:",model.score(standardization, y_0))
输出以下结果:
待判样本类别 [1. 1. 0.] 属于各个样本的概率 [[9.98714907e-01 1.28509280e-03] [9.99936911e-01 6.30890421e-05] [9.99999817e-01 1.83165349e-07] [9.99999976e-01 2.43444948e-08] [9.99971586e-01 2.84135661e-05] [5.37581236e-05 9.99946242e-01] [7.15229062e-04 9.99284771e-01] [2.12967288e-09 9.99999998e-01] [4.15167133e-04 9.99584833e-01] [3.82928356e-06 9.99996171e-01]] 训练样本的回带正确率: 1.0
即第10家公司是ST公司(这是我们已知的),第11家公司也是ST公司,第12家公司不是ST公司
三.一些需要注意的地方
-
MLPRegressor所需要的参数有哪些
这个问题让我先问下Chatgpt
- hidden_layer_sizes:一个整型列表,表示每层隐藏层中神经元的个数。例如,hidden_layer_sizes=(100, 50, 25)表示网络中包含三层隐藏层,每层分别有100、50和25个神经元。
- activation:表示激活函数的类型。默认情况下,MLPRegressor使用“relu”,即“Rectified Linear Unit”激活函数。此外,还可以选择“logistic”、“tanh”等激活函数。
- solver:表示用于训练模型的优化算法。常用的优化算法有“lbfgs”、“sgd”和“adam”。
- alpha:一个浮点数,表示L2正则化项的系数。正则化是一种用于防止过拟合的方法,其中alpha越大,正则化的效果越强。
- learning_rate_init:一个浮点数,表示优化算法的初始学习率。
-
当出现
unsupported operand type(s) for -: 'str' and 'str'这样的报错时,就要考虑转换数据类型#train_x = train_x.apply(pd.to_numeric) #x_min = x_min.apply(pd.to_numeric) #judge_data = judge_data.apply(pd.to_numeric) #x_max = x_max.apply(pd.to_numeric) # 到这数据转换完毕 -
使用pandas提取某几行数据时,使用
df.iloc[]这样提取 -
我们导入的数据应该是这样的,只有x1到x8的数据,没有分类数据
课后作业
例 15.12据研究,某地区的公路客运量主要与该地区的人数、机动车数量和公路面积有关,表15.10所列为该地区1990—2009年20年间公路客运量的相关数据。根据有关部门数据,该地区2010年和2011年的人数分别为73.39万人、75.55万人,机动车数量分别为3.9635万辆、4.0975万辆,公路面积分别为0.9880万m2、1.0268万m。请利用BP神经网络预测该地区2010年和2011年的公路客运量。
| 年份 | 人口数量/万人 | 机动车数量/万辆 | 公路面积/万km2 | 客运量/万人 |
|---|---|---|---|---|
| 1990 | 20.55 | 0.6 | 0.09 | 5126 |
| 1991 | 22.44 | 0.75 | 0.11 | 6217 |
| 1992 | 25.37 | 0.85 | 0.11 | 7730 |
| 1993 | 27.13 | 0.9 | 0.14 | 9145 |
| 1994 | 29.45 | 1.05 | 0.2 | 10460 |
| 1995 | 30.1 | 1.35 | 0.23 | 11387 |
| 1996 | 30.96 | 1.45 | 0.23 | 12353 |
| 1997 | 34.06 | 1.6 | 0.32 | 15750 |
| 1998 | 36.42 | 1.7 | 0.32 | 18304 |
| 1999 | 38.09 | 1.85 | 0.34 | 19836 |
| 2000 | 39.13 | 2.15 | 0.36 | 21024 |
| 2001 | 39.99 | 2.2 | 0.36 | 19490 |
| 2002 | 41.93 | 2.25 | 0.38 | 20433 |
| 2003 | 44.59 | 2.35 | 0.49 | 22598 |
| 2004 | 47.3 | 2.5 | 0.56 | 25107 |
| 2005 | 52.89 | 2.6 | 0.59 | 33442 |
| 2006 | 55.73 | 2.7 | 0.59 | 36836 |
| 2007 | 56.76 | 2.85 | 0.67 | 40548 |
| 2008 | 59.17 | 2.95 | 0.69 | 42927 |
| 2009 | 60.63 | 3.1 | 0.79 | 43462 |
参考解答:
数据地址链接:https://pan.baidu.com/s/1jUsDubJUmvdiipvZdqagZw?pwd=6666
提取码:6666
# coding=utf-8
'''
author:chuanshana
email:2505647237@qq.com
'''
import pandas as pd
from sklearn.neural_network import MLPRegressor
import numpy as np
import pylab as plt
data = pd.read_csv("D:\Pycharm\math_machine\神经网络\某地区公路客运量相关数据.csv", encoding="gbk", index_col=0)
# 同样提取出训练样本数据
train_data = data.iloc[:, :3]
# print(train_data)
y_data = data.iloc[:, 3]
# print(y_data)
# 计算出最大值和最小值
x_min = train_data.min(axis=0)
# print(x_min)
x_max = train_data.max(axis=0)
# print(x_max)
# 进行数据标准化,令我疑惑的一点是这里的y并没有进行标准化
standardization = 2 * ((train_data - x_min) / (x_max - x_min)) - 1
print(standardization)
# 构造并拟合模型
model = MLPRegressor(solver="lbfgs", activation="identity", hidden_layer_sizes=10,
).fit(standardization, y_data) # 这两个参数加不加values都一样
# 根据给出的数据进行预测
given_data = np.array([[73.39, 3.9635, 0.9880], [75.55, 4.0975, 1.0268]])
print(given_data)
xy_min = (x_min.values) # 注意看这里重新计算了一下,提取上面的数值
xy_max = (x_max.values) # 下面也是这样的
given_data_standardization = 2 * (given_data - xy_min) / (xy_max - xy_min) - 1 # 进行数据标准化
y_predict = model.predict(given_data_standardization)
print("预测的数据分别为:", np.round(y_predict, 4)) # 保留四位小数
y_0_predict = model.predict(standardization) # 对测试集进行预测
print("原数据的预测值为:", y_0_predict)
all_predict = list(y_0_predict) + list(y_predict)
# 计算测试集预测值与真实值的误差,百分之多少
delta = abs((y_0_predict - y_data) / y_data) * 100
print("已知数据的相对误差:", np.round(delta, 4))
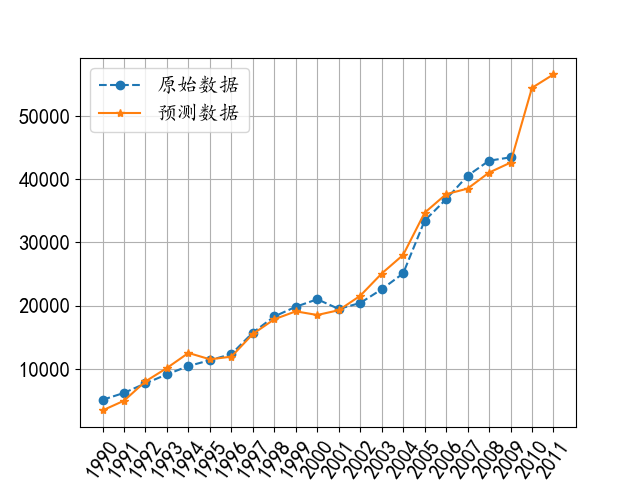
# 可视化:
t = np.arange(1990, 2010)
predict_t = np.arange(1990, 2012)
plt.rc("font", size=15);
plt.rc("font", family="KaiTi")
plt.plot(t, y_data, "--o", label="原始数据")
plt.plot(predict_t, all_predict, "-*", label="预测数据")
plt.xticks(predict_t, rotation=55)
plt.grid(True)
plt.legend()
plt.show()
输出预测值分别为 [54449.6164 56573.6837]
本文参考了司守奎的数学建模算法与应用,由于作者是用的txt格式,所以在数据方面还需琢磨一番。比如的pandas的语法,iloc这些