❓ 剑指 Offer 29. 顺时针打印矩阵

难度：简单

输入一个矩阵，按照从外向里以顺时针的顺序依次打印出每一个数字。

示例 1：

输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[1,2,3,6,9,8,7,4,5]

示例 2：

输入：matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出：[1,2,3,4,8,12,11,10,9,5,6,7]

限制：

• $0<=matrix.length<=100$
• $0<=matrix[i].length<=100$

注意：本题与 54. 螺旋矩阵 相同!

💡思路：模拟

一层一层从外到里打印，观察可知每一层打印都有相同的处理步骤，唯一不同的是上下左右的边界不同了。

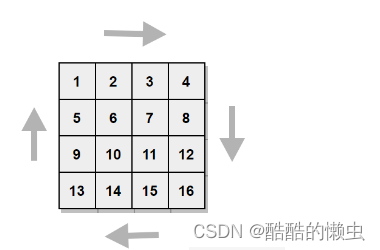
• 因此定义四个变量 up, down , left, right 分别存储上下左右边界值，从而定义当前最外层。

• 循环打印当前最外层的顺序：

  • 从左到右打印最上一行->从上到下打印最右一行->从右到左打印最下一行->从下到上打印最左一行。
    

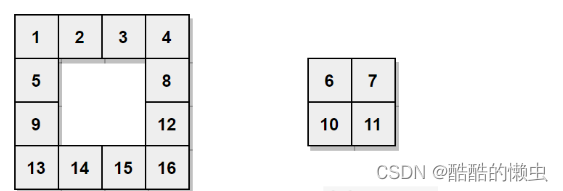
🍁代码：(C++、Java)

C++

class Solution {
public:
    vector<int> spiralOrder(vector<vector<int>>& matrix) {
        int up = 0, down = matrix.size() - 1;
        if(down < 0) return {};
        int left = 0, right = matrix[0].size() - 1;
        vector<int> ans((down + 1) * (right + 1));
        int index = 0;
        while(up <= down && left <= right){
            for(int j = left; j <= right; j++){//往右
                ans[index++] = matrix[up][j];
            }
            if(++up > down) break;//上边界加1
            for(int j = up; j <= down && left <= right; j++){//往下
                ans[index++] = matrix[j][right];
            }
            if(left > --right) break;//右边界减1
            for(int j = right; j >= left && up <= down; j--){//往左
                ans[index++] = matrix[down][j];
            }
            if(up > --down) break;//下边界减1
            for(int j = down; j >= up && left <= right; j--){//往上
                ans[index++] = matrix[j][left];
            }
            if(++left > right) break;//左边界加1
        }
        return ans;
    }
};

Java

class Solution {
    public int[] spiralOrder(int[][] matrix) {
        int up = 0, down = matrix.length - 1;
        if(down < 0) return new int[0];
        int left = 0, right = matrix[0].length - 1;
        int[] ans = new int[(down + 1) * (right + 1)];
        int index = 0;
        while(up <= down && left <= right){
            for(int j = left; j <= right; j++){//往右
                ans[index++] = matrix[up][j];
            }
            if(++up > down) break;//上边界加1
            for(int j = up; j <= down && left <= right; j++){//往下
                ans[index++] = matrix[j][right];
            }
            if(left > --right) break;//右边界减1
            for(int j = right; j >= left && up <= down; j--){//往左
                ans[index++] = matrix[down][j];
            }
            if(up > --down) break;//下边界减1
            for(int j = down; j >= up && left <= right; j--){//往上
                ans[index++] = matrix[j][left];
            }
            if(++left > right) break;//左边界加1
        }
        return ans;
    }
}

🚀 运行结果：

🕔 复杂度分析：

• 时间复杂度：$O(mn)$，其中m 和 n 分别是输入矩阵的行数和列数。矩阵中的每个元素都要被访问一次。
• 空间复杂度：$O(1)$，除了输出数组以外，空间复杂度是常数。

题目来源：力扣。

放弃一件事很容易，每天能坚持一件事一定很酷，一起每日一题吧！
关注我LeetCode主页 / CSDN—力扣专栏，每日更新！

注： 如有不足，欢迎指正！