1. BN层原理

torch.nn.BatchNorm2d(num_features, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True,device=None,dtype=None)

为什么用BN?
加速训练。之前训练慢是因为在训练过程中，整体分布逐渐往非线性函数的取值区间的上下限端靠近(参考sigmoid函数，大的正值或负值)，链式求导导致低层的神经网络梯度消失。BN就是将越来越偏的分布强行拉回(标准)正态分布,使得激活值落在非线性函数对输入比较敏感的区域，这样输入小的变化就会导致损失函数较大变化，让梯度变大，避免梯度消失问题。
为什么要给BN的分布乘以可学习参数 $\gamma$ 和 $\beta$ ?
如果强行归一化为标准正态分布，则之前该层学习到的分布也丢失信息。引入这两个重构参数，来使得我们的网络中可以学习恢复出原始网络要学习的特征分布.
公式(torch):
$\frac{x-E[x]}{\sqrt{Var[x]+\epsilon}}\times \gamma + \beta$
反向传播.
均值和方差是在mini-batch的每一个维度上分别计算的
因为是再 $C$ 维上做的BN，在 $(N, H, W)$ slices, 也就是 计算(N,H,W) 的均值和方差, 因此学术上称为Spatial Batch Normalization.
$\gamma$ 和 $\beta$ 是可学习的参数，尺寸等于input size. 默认 $\gamma$ 设置为1, $\beta$ 设置为0.
标准差是有篇估计, 跟torch.var(input, unbiased=False)相同. $\frac{1}{m}$
训练时, 运行一个计算均值和方差的估计器, 然后再验证阶段做归一化.
推断阶段:
- $\gamma$ , $\beta$ 直接用训练好的.
- 使用均值与方差的无偏估计. 即统计训练中每一个batch的每个维度的均值和方差，然后计算在训练集上的期望:
  $E[x]\leftarrow E_\mathcal{B}[\mu_\mathcal{B}]$
  $\leftarrow \frac{m}{m-1}E_\mathcal{B}[\sigma_\mathcal{B}^2]$
  最终(只是将均值和方差替换，推导一小步即可):
  $\frac{\gamma}{\sqrt{Var[x]+\epsilon}}x+(\beta-\frac{\gamma E[x]}{\sqrt{Var[x]+\epsilon}})$
BN优点汇总:
- 1. 大大提升训练速度，加快收敛
- 1. 提高网络泛化能力，解释是类似于dropout的一种防止过拟合的正则化表达方法，可舍弃dropout
- 1. 调参简单，对初始化要求没那么高，可以加大学习率
- 1. 可以打乱样本训练顺序. 可以提高精度
- 1. BN本质上是一个归一化网络层，可以替代局部响应归一化层(LRN)层
为什么BN层一般用在线性层和卷积层后面，而不是放在非线性单元后？
因为非线性单元的输出分布形状会在训练过程中变化，归一化无法消除他的方差偏移，相反的，全连接和卷积层的输出一般是一个对称,非稀疏的一个分布，更加类似高斯分布，对他们进行归一化会产生更加稳定的分布。其实想想也是的，像relu这样的激活函数，如果你输入的数据是一个高斯分布，经过他变换出来的数据能是一个什么形状？小于0的被抑制了，也就是分布小于0的部分直接变成0了，这样不是很高斯了。
缺点:
需要一个足够大的批量，小的批量会导致对批统计数据的不准确性提高，显著增加模型错误率。即BN收到batch影响很大. 例如检测和分割任务.

2. LayerNorm原理(LN)

torch.nn.LayerNorm(normalized_shape, eps=1e-05, elementwise_affine=True, device=None, dtype=None)

公式:
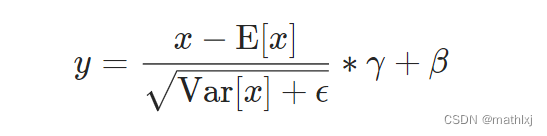
均值和方差的计算与BN相似，只是维度由normalized_shape决定，例如为(3,5),则在最后两个维度.
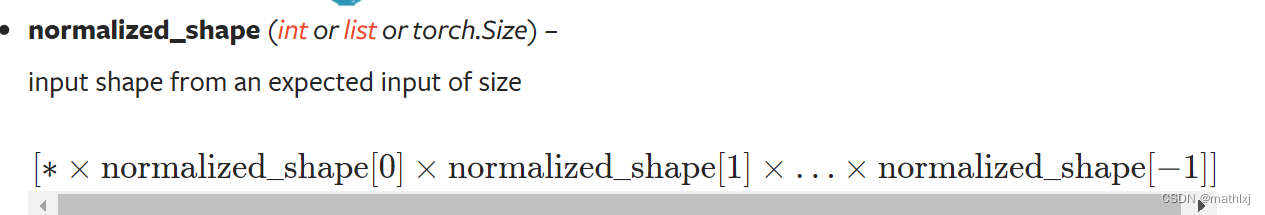
一个图像的例子，在C,H,W上做归一化

在CV中，沿着 $(C, H, W)$ 做归一化.

3. Instance Normlization (IN)和 Group Normalization (GN)

IN: 沿着 $(H, W)$ 轴计算，每个样本单独计算，每个channel单独计算
GN: 对channel分组进行计算， C/G为每组的通道数，沿着 $(X / G, H, W)$ 来计算
- 当G=1时，变成了LN。GN比LN受限制更少，因为假设每组通道（而不是所有通道）都受共享均值和方差的影响; 该模型仍然具有为每个群体学习不同分布的灵活性。这导致GN相对于LN的代表能力提高。
- 当G=C时，变成了GN. 但是IN只能依靠空间维度来计算均值和方差，并且错过了利用信道依赖的机会。