【Python统计与数据分析实战_01】位置与分散程度的度量

news2024/7/6 6:14:23

数据描述性分析

  • 1.描述统计量
    • 1.1 位置与分散程度的度量
      • 1.1.1 例子一 单维数组
      • 1.1.2 例子二 多维数组
    • 1.2 关系度量
    • 1.3 分布形状的度量
      • 1.3.1 统计量：偏度和峰度
  • 1.4 数据特性的总括

1.描述统计量

数据的统计分析分为统计描述和统计推断两部分。前者通过绘制统计图、编制统计表、计算统计量等方法表述数据的分布特征，是数据分析的基本步骤，也是统计推断的基础。其优点在于方便、直观，利于对数据特征的理解。

1.1 位置与分散程度的度量

数据是信息的载体，从数据到信息，需要先分析数据的主要特征，这些特征包括数据的位置度量、分散程度度量、关系度量以及分布形状的度量。

1、均值：数据的平均值。
在这里插入图片描述
2、中位数：一组数据中间位置的数。
在这里插入图片描述
3、百分位数：如果将一组数据从小到大排序，并计算相应的累计百分位，则某一百分位所对应数据的值就称为这一百分位的百分位数。

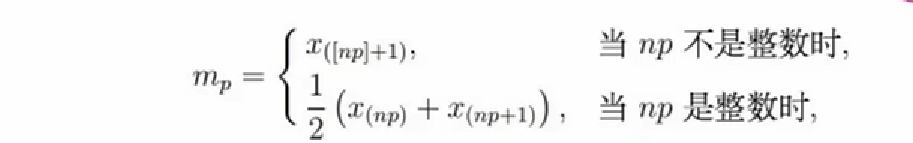
在这里插入图片描述
4、方差：用来衡量样本偏离均值的程度，或者描述数据取值分散性程度一个度量。

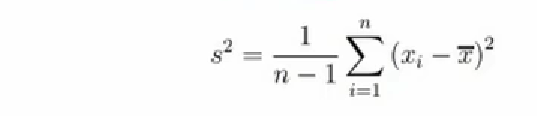
在这里插入图片描述

5、标准差：方差的算术平方根，用o表示。标准差也被称为标准偏差，或者实验标准差，在概率统计中最常使用作为统计分散分布程度上的测量依据。

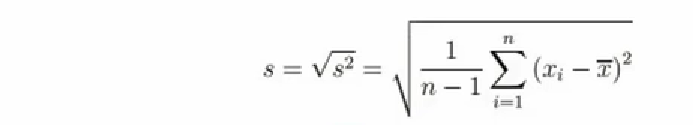
在这里插入图片描述

6、标准误：描述平均数抽样分布的离散程度及衡量平均数拙样误差大小的尺度，反映样本平均数之间的变异。

在这里插入图片描述

1.1.1 例子一 单维数组

import numpy as np
import scipy.stats as st 
import pandas as pd 
import statsmodels.api as sm 
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.sans-serif']=['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False # 用来正常显示符号

'''
示例：某学校15个学生体重（单位：公斤）抽样调查数据
'''
weights=np.array([75.0,64.0,47.4,66.9,62.2,62.2,58.7,63.5,66.6,64.0,57.0,69.0,56.9,50.0,72.])

# 数组里面求均值
w_mean=np.mean(weights)
w_mean1=weights.mean()
print(w_mean)
print(w_mean1)

#限定范围内的数据求均值
limitedMean=st.tmean(weights,(60,70))
# 表示对weights的变量进行截断，即排除小于60的和大于70的数据，只计算包含60,70以及之间数据的平均值
print(limitedMean)

# 对数组进行排序
sorted_weig=sorted(weights,reverse=True)#reverse的缺省值为False
print(sorted_weig) # 结果为降序排列

# 中位数
# 对称分布比如t分布和正态分布，均值与中位数很接近；偏态分布的两者相差比较大
median_weig=np.median(weights)
print(median_weig)

# 分位数
quantiles=np.quantile(weights,[0.1,0.2,0.4,0.6,0.8,1])
print('学生体重的[10%,20%,40%,60%,80%,100%]分位数：',quantiles)

在这里插入图片描述

# 注意方差与方差的无偏估计之间的计算区别
v=np.var(weights)#有偏估计或样本方差
v_unb=st.tvar(weights)#无偏估计
print('体重数据方差的估计为:%0.2f,无偏估计为:%0.2f'%(v,v_unb))

在这里插入图片描述

# 注意标准差与标准差的无偏估计之间的计算区别
s=np.std(weights)#有偏估计或样本标准差
s_unb=st.tstd(weights)#无偏估计
print('体重数据标准差的估计为：%0.2f,无偏估计为：%0.2f'%(s,s_unb))

在这里插入图片描述

cv=s_unb/w_mean*100 #变异系数为标准差/平均数，无量纲，用百分数表示
print('体重数据的变异系数为：',np.round(cv,2),'%')

在这里插入图片描述

#极差与标准误
R_weights=np.max(weights)-np.min(weights)#极差：最大值-最小值
print('体重数据的极差：%0.2f'%R_weights)
sm_weights=st.tstd(weights)/np.sqrt(len(weights))#标准误：数据标准差（无偏）/数据量**0.5
print('体重数据的标准误：%0.2f'%sm_weights)

在这里插入图片描述

1.1.2 例子二 多维数组

#身高(这里我试过了，如果不换行的话，后面转置会出错)
x1=np.array([148, 139, 160, 149, 159, 142, 153, 150, 151, 139, 
        140, 161, 158, 140, 137, 152, 149, 145, 160, 156, 
        151, 147, 157, 147, 157, 151, 144, 141, 139, 148]) 
#体重
x2=np.array([41, 34, 49, 36, 45, 31, 43, 43, 42, 31, 
        29, 47, 49, 33, 31, 35, 47, 35, 47, 44,
        42, 38, 39, 30, 48, 36, 36, 30, 32, 38])
#胸围
x3=np.array([72, 71, 77, 67, 80, 66, 76, 77, 77, 68, 
        64, 78, 78, 67, 66, 73, 82, 70, 74, 78, 
        73, 73, 68, 65, 80, 74, 68, 67, 68, 70])
#坐高
x4=np.array([78, 76, 86, 79, 86, 76, 83, 79, 80, 74, 
        74, 84, 83, 77, 73, 79, 79, 77, 87, 85, 
        82, 78, 80, 75, 88, 80, 76, 76, 73, 78])
#将x1,x2,x3,x4四个向量合并存储为矩阵，并转置为列向量，.T操作符（或属性）是对矩阵进行转置。
stu_data = np.matrix([x1,x2,x3,x4]).T 
print('学生的身高、体重、胸围和坐高（前五个）：\n',stu_data[0:5])

stu_mean = np.round(stu_data.mean(0),1).ravel()#将二维矩阵展平为一维向量,数据类型转变为Numpy数组
'''
注意stu_data.mean(0)的用法，通过Numpy的函数生成数据对象，Numpy很多函数就会注入数据中，此处直接调用数据对象的函数求平均值。函数的参数0表示列向量方向，如果为1则是行向量方向。
也可以这样调用：np.mean(stu_data,axis=0),%%javascript果一样。
其他统计量计算类似。
'''
print('\n学生的平均身高、平均体重、平均胸围和平均坐高分别为：\n %.1f, %.1f, %.1f, %.1f,' 
      %(stu_mean[0],stu_mean[1],stu_mean[2],stu_mean[3]))

在这里插入图片描述

1.2 关系度量

在统计当中对数据的关系进行度量，主要是使用协方差矩阵与相关系数来进行计算的。

1、方差-协方差矩阵
协方差表示两个变量的总体的误差。如果两个变量的变化趋势一致，也就是说如果其中一个大于自身的期望值，另外一个也大于自身的期望值，那么两个变量之间的协方差就是正值。如果两个变量的变化趋势相反，即其中一个大于自身的期望值，另外一个却小于自身的期望值，那么两个变量之间的协方差就是负值。多个样本之间的协方差构成协方差矩阵。
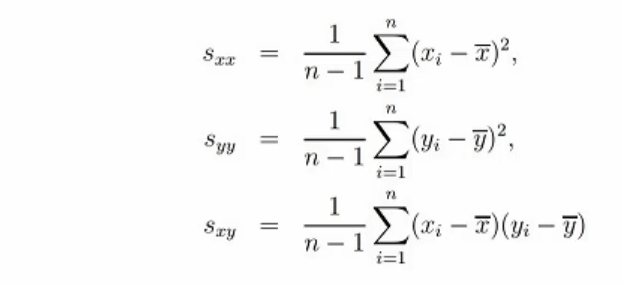
在这里插入图片描述

2、相关系数矩阵
相关系数是最早由统计学家卡尔·皮尔逊设计的统计指标，是研究变量之间线性相关程度的量，一般用字母r表示。由于研究对象的不同，相关系数有多种定义方式，较为常用的是皮尔逊(Pearson)相关系数。多个样本之间的相关系数构成相关系数矩阵,使用R或ρ表示。
在这里插入图片描述

'''
求四个向量之间的方差-协方差矩阵时，需要对矩阵进行转置，将列向量转换成行向量。
求相关系数矩阵时同样也要进行转置，相关系数矩阵是协方差矩阵进行标准化转换之后的结果。
'''
### 协方差矩阵：covariance和
cov_stu=np.cov(stu_data.T)# 方差-协方差矩阵
### 相关系数矩阵：correlation coefficient
rou_stu=np.corrcoef(stu_data.T)

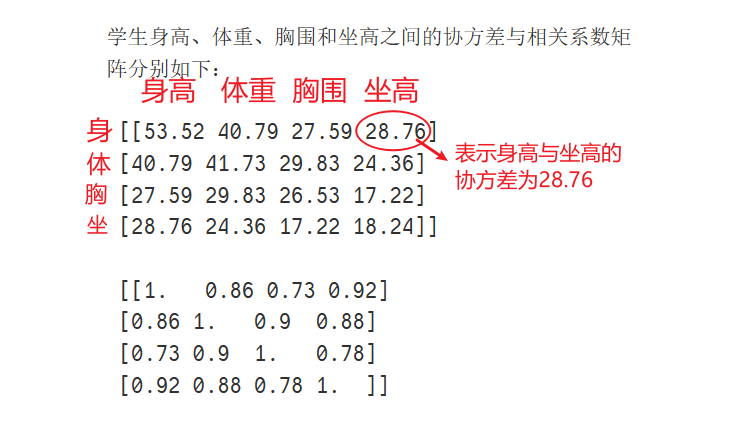
#结果显示，四个随机向量之间的相关程度很高，尤其是身高和坐高之间的相关性最高（0.92）。
print('学生身高、体重、胸围和坐高之间的协方差与相关系数矩阵分别如下：\n\n',np.round(cov_stu,2),'\n\n',np.round(rou_stu,2))
# round表示进行四舍五入操作，只保留两位小数

协方差的数据都是正值，表示这四个变量之间是正相关的关系。
在这里插入图片描述

1.3 分布形状的度量

1.3.1 统计量：偏度和峰度

偏度是统计数据分布偏斜方向和程度的度量，是统计数据分布非对称程度的数字特征。
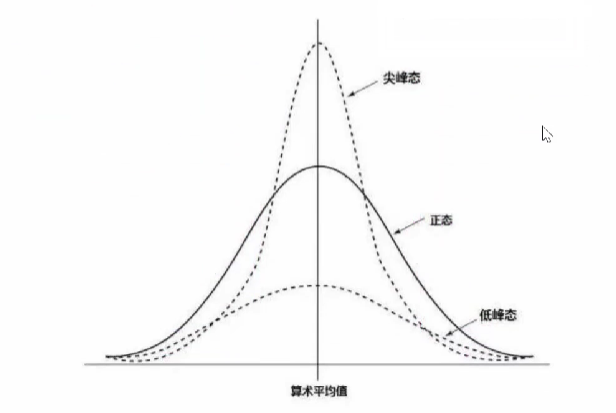
峰度表征概率密度分布曲线在平均值处蝮值高低的特征数。直观看来，峰度反映了峰部的尖度。

1、偏态：

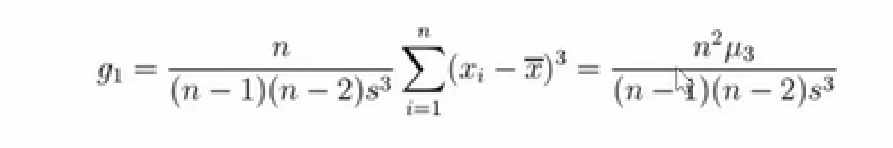
在这里插入图片描述
2、峰态：

在这里插入图片描述
3、偏度计算公式：

在这里插入图片描述

4、峰度计算公式：
在这里插入图片描述

在这里插入图片描述

'''
偏度计算： 
（1）偏度表示曲线是向左偏或右偏，又称正偏态或者负偏态。
（2）偏度越接近于0，越符合正态分布的曲线。
（3）偏度小于0则称分布具有负偏离，也称左偏态；反之就是右偏态或正偏态。
'''
### 偏态计算公式
n=len(weights)
# 三阶矩，其他各阶矩的计算一次类推
u3=np.sum((weights-w_mean)**3)/n # **表示乘方
### 使用总体标准差的无偏估计，计算的偏度是修正后的偏度
skew1=((n**2)*u3)/((n-1)*(n-2)*(s_unb**3))

###调用pandas包当中的skew()来计算偏度，这时需要把weights先转化为pd.Series之后再掉包：
pd_weights=pd.Series(weights)
skew_pandas=pd_weights.skew()
print('Pandas计算公式手工计算以及调用函数计算的结果：')
print('skew1:',skew1,'skew_pandas:',skew_pandas)

在这里插入图片描述

###无修正偏度的手工计算，使用样本标准差
skew2=np.sum((weights-w_mean)**3)/((s**3)*n)

### scipy计算公式和结果
print('\nScipy计算公式手工计算以及调用函数计算的结果（无修正）：')
skew_scipy=st.skew(weights)
print('skew2:',skew2,'skew_scipy',skew_scipy)
'''
(1)使用Scipy的skew函数，如果将第二个参数bias设为False,则计算结果就和Pandas完全相同了。bias参数表示是否修正，如果为False表示修正，反之则不修正。
（2）总体上感觉修正后的偏度比较准确，但是很多场合仍用无修正的偏度进行统计量的计算。
（3）StatsModels的线性回归模型对残差的正态分布性（Jarque-Bera、Omnibus检验等）进行检验时，使用的偏度就是无修正的，包括峰度也是无修正的。
'''
skew_scipy_bias=st.skew(weights,bias=False)
print('\nScipy进行修正后的偏度：',skew_scipy_bias)

在这里插入图片描述

在这里插入图片描述

'''
峰度的计算：
（1）峰度表示曲线是扁平态（低峰态）还是尖峰态
（2）正常值有两种定义：Fisher定义该值为0；Person定义为3。
（3）按照Fisher定义，峰度=0表示正好符合正态分布曲线；大于0表示峰比较尖，反之表示比较平。
'''
###峰度计算，StatsModels多使用无修正的峰度
kurt_pandas=pd_weights.kurt()#pandas计算出来的峰度是有修正的
kurt_scipy=st.kurtosis(weights,bias=False)#True是bias的缺省值
kurt_scipy_bias=st.kurtosis(weights,bias=True)
print('\nPandas计算峰度：',kurt_pandas,'\nScipy计算峰度（修正后）：',kurt_scipy,'\n\nScipy计算峰度（无修正）：',kurt_scipy_bias)

在这里插入图片描述

1.4 数据特性的总括

'''
数据总括：
（1）数据特性总括，包括：最小最大值、均值、方差、偏度、峰度。
（2）此处使用了修正选项，偏度和峰度都是修正后的值。
（3）数据分布的正态性检验与分布拟合检验。
'''
print('学生体重数据的总括概述：',st.describe(weights,bias=False))
'''
正态性检验：主要考察p值，如果p值>0.05，则不能拒绝原假设，即数据服从正态分布。
此处p值=0.837，远大于0.05，说明体重数据服从正态分布性。
最常用的函数是夏皮罗(shapiro)%hist数检验。
Scipy包含多种正态分布检验的函数。
'''
print('\n学生体重数据的正态性检验：',st.shapiro(weights))
print('\n测试不服从正态分布的数据：',st.shapiro([1,2,3,4,900]))#p值远小于0.05，拒绝原假设

在这里插入图片描述

'''
经验分布的检验方法：概率分布Kolmogorov-Smirnov检验法
改该函数检验数据是否服从某个类型的概率分布函数，不仅仅是正态生成一个服从分布的测试分布。
kstest函数原假设两个独立样本数据来自同一个连续分布。
生成一个服从F分布的测试数据：
（1）第一个函数测试其是否服从自由度为3的t分布；
（2）第二个函数测试是否服从自由度为2,9的F分布；
'''
#生成服从f分布，自由度为（2,9）的随机数据
f_data=st.f.rvs(size=50,dfn=2,dfd=9)
#检验上述数据是否服从自由度为3的t分布，结果很显然拒绝服从该分布的原假设
print('\n检验数据是否服从某种分布：',st.kstest函数原假设两个独立样本数据来自同一个连续分布。(f_data,'t',(3,)))#(3,)表示t分布的自由度
print('\n检验数据是否服从某种分布：',st.kstest(f_data,'f',(2,9)))#接受原假设服从自由度为2,9的f分布

在这里插入图片描述
在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/767430.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Vue3.0的设计目标是什么？做了哪些优化?

Vue3.0的设计目标是什么？做了哪些优化?

一、设计目标 不以解决实际业务痛点的更新都是耍流氓，下面我们来列举一下Vue3之前我们或许会面临的问题 随着功能的增长，复杂组件的代码变得越来越难以维护 缺少一种比较「干净」的在多个组件之间提取和复用逻辑的机制 类型推断不够友好 bundle的时间太久了 而 Vue3 经过长达…
阅读更多...
RuoYi-Vue/vue项目访问 webpack 中定义的变量

RuoYi-Vue/vue项目访问 webpack 中定义的变量

前言 RuoYi-Vue 3.8.4 webpack 中定义的变量 vue.config.js 中定义的 webpack 的变量 在html页面中&#xff0c;如何访问 webpack 的变量 <title><% webpackConfig.name %></title>参考&#xff1a;ruoyi-ui/public/index.html 文件
阅读更多...
【分布式训练】基于Pytorch的分布式数据并行训练

【分布式训练】基于Pytorch的分布式数据并行训练

基于Pytorch的分布式数据并行训练 动机为什么要并行分布数据&#xff1f;现有资料的不足 Outline整体框架图带解释的最小demo示例没有multiprocessing开启multiprocessing 分布式训练启动方式混合精度训练&#xff08;采用apex&#xff09; 参考资料 简介&#xff1a; 在PyTorc…
阅读更多...
一则 MySQL 参数设置不当导致复制中断的故障案例

一则 MySQL 参数设置不当导致复制中断的故障案例

本文分享了一个数据库参数错误配置导致复制中断的问题&#xff0c;以及对参数配置的建议。 作者&#xff1a;秦福朗 爱可生 DBA 团队成员&#xff0c;负责项目日常问题处理及公司平台问题排查。热爱互联网&#xff0c;会摄影、懂厨艺&#xff0c;不会厨艺的 DBA 不是好司机&…
阅读更多...
Linux学习之运算符

Linux学习之运算符

是赋值运算符&#xff0c;可以把一个变量设置上特定的值&#xff0c;而算术运算符就包括加减乘除&#xff08;、-、*、/&#xff09;&#xff0c;需要使用expr这个命令进行运算。 expr 5 7可以计算出来5与7的和&#xff0c;使用echo $?可以看到expr 5 7这个命令的返回值是0&…
阅读更多...
神经网络正则化之BN/LN/GN的原理

神经网络正则化之BN/LN/GN的原理

1. BN层原理 torch.nn.BatchNorm2d(num_features, eps1e-05, momentum0.1, affineTrue, track_running_statsTrue,deviceNone,dtypeNone) 为什么用BN? 加速训练。之前训练慢是因为在训练过程中&#xff0c;整体分布逐渐往非线性函数的取值区间的上下限端靠近(参考sigmoid函数…
阅读更多...
10.6.5 【Linux】分区命令： split

10.6.5 【Linux】分区命令： split

如果你有文件太大&#xff0c;导致一些携带式设备无法复制的问题&#xff0c;split可以将一个大文件&#xff0c;依据文件大小或行数来分区&#xff0c;可以将大文件分区成为小文件&#xff0c;快速有效。 将文件分区的话&#xff0c;使用-b size来将一个分区的文件限制其大小&…
阅读更多...
软件测试岗位之我所思我所见

软件测试岗位之我所思我所见

从业以来&#xff0c;见过很多人&#xff0c;看过很多事。唯独“测试”我觉得是我自己选的路。所以现在这个时间点&#xff0c;我想分享下我对测试的看法&#xff1a; 1、测试 &#xff1a;“轻松” “劳累” 作为一个测试&#xff0c;你可以轻松的没有下限&#xff0c;也可…
阅读更多...
重写equals为什么要重写hashCode(配合源码分析)

重写equals为什么要重写hashCode(配合源码分析)

目录 一、hashCode的概念 二、为什么要有hashCode 三、为什么重写equals要重写hashCode 四、HashSet源码分析 五、容易记混的点 一、hashCode的概念 hashCode()是Object定义的方法&#xff0c;它将返回一个整型值&#xff0c;这个方法通常用来将对象的内存地址转换为整数之…
阅读更多...
postman批量执行请求，通过json传参

postman批量执行请求，通过json传参

1、创建请求 "authUid":"{{authUid}}", 加粗为需要替换的参数 2、组装JSON 可通过Excel自动填充功能构造数据 [ {"authUid":"18700000001"}, {"authUid":"18725929202"} ] 3、批量执行请求配置 4、然后start r…
阅读更多...
「网络编程」传输层协议_ UDP协议学习_及原理深入理解

「网络编程」传输层协议_ UDP协议学习_及原理深入理解

「前言」文章内容大致是传输层协议&#xff0c;UDP协议讲解。 「归属专栏」网络编程 「主页链接」个人主页 「笔者」枫叶先生(fy) 目录 一、传输层二、UDP协议2.1 再谈端口号2.2.1 端口号范围划分2.2.2 认识知名端口号2.2.3 端口号注意问题2.2.4 netstat命令和pidof命令 2.2 UD…
阅读更多...
实时数据集成的完美搭档：CDC技术与Kafka集成的解决方案

实时数据集成的完美搭档：CDC技术与Kafka集成的解决方案

目录 一、实时数据同步 二、可靠的数据传输 三、灵活的数据处理 四、解耦数据系统 五、主流免费CDC工具介绍 六、Flink CDC安装使用步骤&#xff1a; 七、ETL CDC安装使用步骤 八、写在最后 一、实时数据同步 随着企业数据不断增长&#xff0c;如何高效地捕获、同步和…
阅读更多...
如何将视频音频提取出来？这几个方法真的实用！

如何将视频音频提取出来？这几个方法真的实用！

在视频制作和后期处理中&#xff0c;有时我们需要将视频中的音频提取出来&#xff0c;以便单独处理&#xff0c;如剪辑、增强声音等&#xff0c;而不影响视频内容。为了帮助您实现这一目标&#xff0c;下面将介绍几种常用的方法来提取视频音频。 方法一&#xff1a;记灵在线工…
阅读更多...
SSH服务（二十六）

SSH服务（二十六）

提示&#xff1a;文章写完后&#xff0c;目录可以自动生成&#xff0c;如何生成可参考右边的帮助文档 目录 前言 一、概述 二、特点 三、身份验证机制 四、验证过程 五、加密机制 六、基本参数 ​七、 身份验证机制 八、基本操作 1. ssh 2. scp 3. sftp 4. 密钥对验证 总结 前…
阅读更多...
vue或react当中canvas实现电子签名组件和使用canvas进行图片压缩

vue或react当中canvas实现电子签名组件和使用canvas进行图片压缩

<template><div><h1>vue3</h1><canvas id"canvasWrite"> 浏览器不支持Canvas,请升级浏览器 </canvas><div><button class"submit" click"submitWrite">提交签名</button><button clas…
阅读更多...
DOM学习

DOM学习

1.DOM 简介 1.1 什么是 DOM 文档对象模型&#xff08;Document Object Model&#xff0c;简称 DOM&#xff09;&#xff0c;是 W3C 组织推荐的处理可扩展标记语言&#xff08;HTML 或者XML&#xff09;的标准编程接口。 W3C 已经定义了一系列的 DOM 接口&#xff0c;通过这些…
阅读更多...
Spring项目创建与Bean的存储与读取(DL)

Spring项目创建与Bean的存储与读取(DL)

文章目录 一. Spring项目的创建1. 创建Maven项目2. 配置国内源3. 添加spring依赖4. 创建启动类 二.储存或读取Bean对象1. 添加spring配置文件2. 创建Bean对象3. 读取Bean对象 一. Spring项目的创建 1. 创建Maven项目 第一步&#xff0c;创建 Maven 项目&#xff0c;Spring 也…
阅读更多...
LAZYSYSADMIN1靶机详解

LAZYSYSADMIN1靶机详解

LAZYSYSADMIN1靶机复盘 一个五分钟就能结束的靶机&#xff0c;非常快。 下载地址&#xff1a;https://download.vulnhub.com/lazysysadmin/Lazysysadmin.zip nmap对这个ip进行单独扫描后发现开启的服务挺多。 就直接枚举了一下这个服务器的内容&#xff0c;发现了一个用户名…
阅读更多...
试验数据管理平台解决方案-MDM

试验数据管理平台解决方案-MDM

试验是汽车研发、生产制造和售后保障过程中必不可少的重要环节。试验员曾到过寒区、热区、高原、沙漠和山路等恶劣环境下的场地来对试验车辆进行相关试验。这是因为汽车在不同的道路、地理和气候条件下行驶时&#xff0c;其性能、效率、可靠性和耐久性等技术特性也会发生变化。…
阅读更多...
2023四大进销存软件推荐，第一款适合中小商户使用！

2023四大进销存软件推荐，第一款适合中小商户使用！

在当今竞争激烈的商业环境中&#xff0c;企业或商户迫切需要使用进销存管理软件&#xff0c;来优化库存控制、提高运营效率、降低成本&#xff0c;并加强与供应链合作伙伴之间的协作和沟通。 为了帮助企业选择适合自己需求的进销存软件&#xff0c;我们特别整理了2023年市面上比…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023